Математическая модель системы автоматического управления температурой жидкости на выходе теплообменника-смесителя проточного типа

метки: Управление, Автоматический, Система, Смеситель, Модель, Математический, Температура, Холодное

В курсовой работе приведена математическая модель системы автоматического управления температурой жидкости на выходе теплообменника-смесителя проточного типа, проведено ее исследование и определены тип и рациональные значения параметров настройки регулятора.

Два потока жидкофазных теплоносителей подаются в аппарат, где происходит их перемешивание при помощи, погруженной в смесь крыльчатки. В результате этого процесса получается смесь необходимой температуры, которая затем отводится из аппарата. Управление процессом осуществляется путем изменения расхода 2-го (холодного) теплоносителя.

Модель получена при следующих ограничениях:

ü теплообмен аппарата со средой пренебрежимо мал.

Исполнительный механизм — электрический.

Принципиальная схема регулирования температуры жидкости на выходе теплообменника-смесителя проточного типа представлена

на рисунке 1.

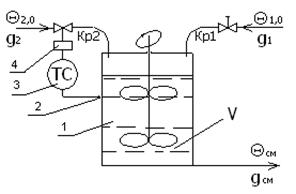
Рисунок 1 — Принципиальная схема регулирования температуры: 1 — резервуар; 2 — датчик температуры; 3 — регулятор; 4 — исполнительное устройство

Функциональная схема регулирования уровня жидкости в резервуаре представлена на рисунке 2.

Объект регулирования — кран линии подачи холодного теплоносителя Кр1 (рисунок 1).

Рабочее тело — жидкофазный теплоноситель.

Регулируемый параметр — температура жидкости на выходе аппарата Θ _см (рисунок 1).

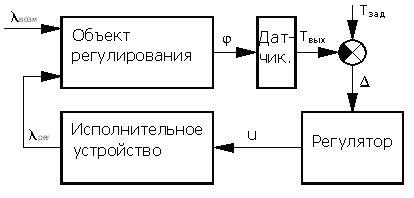
Рисунок 2 — Функциональная схема системы автоматического управления температурой жидкости на выходе из теплообменника: λ _возм — возмущающее воздействие; λ_рег — регулирующее воздействие; Т_вых — сигнал температуры жидкости на выходе аппарата; Т_зад — сигнал заданной температуры смеси; Δ — рассогласование; u — сигнал управления

Энергия в химическом производстве и массообменные процессы в аппаратах

... Использование энергии в химической промышленности Химическое производство принадлежит к числу наиболее энергоемких. Так, если в продукции всей промышленности доля затрат на энергию составляет 2,5%, то в продукции нефтехимической и химической отраслей она достигает 8,9%. Химическая отрасль промышленности, ...

Значения параметров объекта регулирования:

Θ _1,0 — температура горячего (1-го) теплоносителя 100 ˚С;

Θ _2,0 — температура холодного (2-го) теплоносителя 10 ˚С;

Θ _см — заданная температура смеси 40 ˚С;

С ₁ — теплоемкость первого теплоносителя 1000 кал/(кг·град);

С ₂ — теплоемкость второго теплоносителя 580 кал/(кг·град);

С _см — теплоемкость смеси 620 кал/(кг·град);₁ — расход (номинальный) первого теплоносителя 0,008333 м³ /с;₂ — расход (номинальный) второго теплоносителя 0,006944 м³ /с;- объем зоны перемешивания 12 м³ ;

• Ведущим является расход 2-го (холодного) теплоносителя.

Датчик температуры формирует на выходе сигнал напряжения, пропорциональный значению температуры жидкости на выходе аппарата.

Регулятор представляет собой типовой электрический ПИД-регулятор, на вход которого поступает сигнал рассогласования, сформированный элементом сравнения «ЭС», как разность сигналов датчика и задатчика, а на его выходе формируется управляющий сигнал в границах ±10 В.

Математическая логическая аналитическая модель системы автоматического управления состоит из математической модели объекта регулирования, математической модели датчика температуры, математической модели элемента сравнения, математической модели регулятора, математической модели исполнительного

Объект регулирования рассматривается как одноемкостной и может быть описан дифференциальным уравнением первого порядка вида:

,

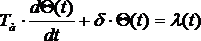Где Т _а — постоянная времени (время разгона) объекта;

• Θ — относительная величина регулируемого параметра;
• δ — коэффициент самовыравнивания объекта;
• λ — относительная величина возмущающего воздействия.

Для составления аналитической модели необходимо связать параметры дифференциального уравнения: время разгона объекта и коэффициент самовыравнивания с физическими параметрами объекта.

Изменение температуры жидкости в теплообменнике зависит от:

1. количества теплоты, вносимой в резервуар горячим теплоносителем;

2. количества теплоты, вносимой в резервуар холодным теплоносителем;

• количества теплоты, уносимого из резервуара выходным потоком.

Объемный расход горячего носителя, температуры входных потоков, а также объем зоны перемешивания принимаются постоянными. Следует иметь в виду, что теплоемкость, плотность и температура выходного потока равны теплоемкости, плотности и температуре среды, находящейся в аппарате.

Исходя из вышеизложенных допущений, а также из уравнений теплового и материального балансов записывается уравнение, определяющее скорость изменения выходной температуры:

,

Математические схемы вероятностных автоматов

... типовые математические схемы: дифференциальные уравнения, конечные и вероятностные автоматы, системы массового обслуживания, сети Петри. Не обладая такой степенью общности, как рассмотренные модели, типовые математические схемы имеют ... которое подаются входные сигналы и снимаются выходные и которое может иметь некоторые внутренние состояния. В общем виде вероятностный автомат можно определить как ...

где ;

;

.

гдеΘ _1,0 — температура горячего потока 100 ˚С;

Θ _2,0 — температура холодного потока 10 ˚С;

Θ _см — температура выходного потока 40 ˚С;

С ₁ — теплоемкость первого теплоносителя 1000 кал/(кг·град);

С ₂ — теплоемкость второго теплоносителя 580 кал/(кг·град);

Рассчитаем температуру теплоносителя в ёмкости в начальный момент времени:

Отклонение температуры жидкости на выходе теплообменника-смесителя от заданного значения возникает вследствие колебания температуры холодного теплоносителя.

Т → Т _ВЫХ ,

Где Т — температура жидкости на выходе, °С;

Т _ВЫХ — сигнал датчика, В.

На объекте использован датчик температуры, передаточная функция которого имеет вид:

Примем k _Д = 1 [°С/В].

(Т _ВЫХ — Т_ЗАД ) →Δ,

Где Т _ВЫХ — сигнал датчика, В;

Т _ЗАД — сигнал задатчика, В;

• Δ — сигнал рассогласования, В.

Передаточная функция звена сравнения будет иметь вид:

Δ → u,

Где Δ — сигнал рассогласования, В;

• u — сигнал управления, В.

В модели используется ПИД-регулятор, математическая модель которого имеет вид:

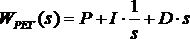
Математическая модель исполнительного устройства состоит из математической модели согласующего устройства, математической модели электродвигателя, математической модели редуктора, математической модели механизма привода штока вентиля.

Математическая модель исполнительного устройства в целом имеет вид:

u → Х _ШТ ,

где u — сигнал управления, В;

Х _ШТ — перемещение штока вентиля, м.

Передаточная функция исполнительного устройства в целом имеет вид:

.

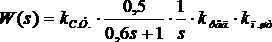u → f,

где u — сигнал управления, В;

• f — частота тока питающей сети, Гц.

Передаточная функция звена имеет вид:

k _СУ = f / u = 50 / 10 = 5 [Гц/В].

f → n,

где f — частота тока питающей сети, Гц;

• n — частота вращения ротора двигателя, об/с.

В качестве электродвигателя будем использовать асинхронный четырех полюсный двигатель, для которого синхронная частота вращения ротора n при частоте тока питающей сети f = 50 Гц равна 25 об/c, а зависимость частоты вращения ротора от частоты тока питающей сети линейная.

Двигатель для схемы (f → n) представляет собой звено первого порядка, передаточная функция которого имеет вид:

.

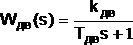Коэффициент передачи для двигателя в этом случае равен:

k _дв = n / f = 25 / 50 = 0,5

Постоянную времени для электродвигателей можно определить по моментам инерции, либо маховым моментам ротора, приводимым в каталогах. Для асинхронных трехфазных двигателей единой серии мощностью 0,6…1,5 кВт постоянную времени Т _ДВ можно принимать в пределах от 0,6…1,8 с.

Однако для дальнейшего использования нам необходимо получить преобразование несколько другого вида:

f → ψ ₁ ,

где f — частота тока питающей сети, Гц;

ψ ₁ — угол поворота якоря двигателя, об.

В этом случае передаточная функция примет вид:

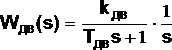
Ограничим перемещение штока вентиля до 0,5 D _у , для чего используем интегратор «с насыщением».

ψ ₁ → ψ₂ ,

где ψ ₁ — угол поворота якоря двигателя, об;

ψ ₂ — угол поворота выходного вала редуктора, об.

Передаточная функция имеет вид:

Полагаем, что редуктор привода настраиваемый, поэтому модель привода должна содержать настройку.

ψ ₂ → Х_ШТ ,

где ψ ₂ — угол поворота выходного вала редуктора, об;

Х _ШТ — перемещение штока вентиля, м.

Передаточная функция имеет вид:

Будем считать, что перемещение штока вентиля производится механизмом «винт-гайка». Шаг гайки h примем равным 0,004 м. Тогда k _п.шт = 0,004 м/об.

μ → λ,

где λ — возмущающее воздействие.

Возмущающим воздействием для объекта регулирования является λ(t) — относительное возмущение, которое складывается из двух возмущений: колебаний температуры холодного теплоносителя λ ₁ (t) и температуры горячего теплоносителя λ₂ (t):

Модель реализована в пакете Matlab, при этом использован инструмент визуального моделирования Simulink.

Общая схема инструментальной модели системы автоматического регулирования уровня жидкости в емкости состоит из подсистем, которые представлены четырьмя инструментальными моделями:

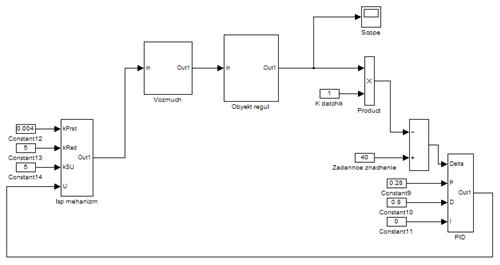
Рисунок 3 — Инструментальная модель объекта регулирования

Рисунок 4 — Инструментальная модель объекта регулирования

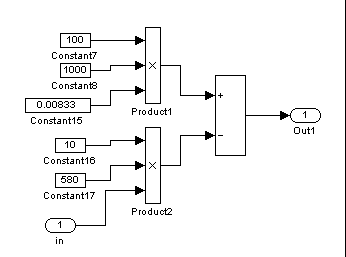
Рисунок 5 — Инструментальная модель формирователя возмущений

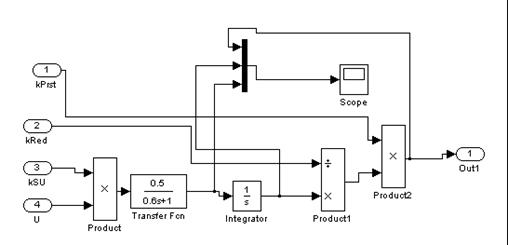
Рисунок 6 — Инструментальная модель исполнительного устройства

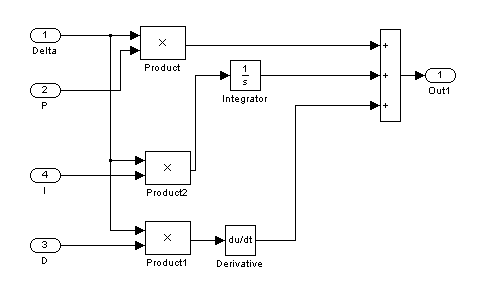
Рисунок 7 — Инструментальная модель регулятора

Подбираем вручную параметры регулирования P, I, D для обеспечения удовлетворительного результата регулирования.

В ходе ручного подбора установлено, что удовлетворительными параметры являются:

ü P = 0,5

ü I = 0

ü D = 1

Производим оптимизацию с переходом по первому улучшению, полученные данные записываем в таблицу 1. Наилучшим считаем результат при наименьшем времени регулирования (t _рег ) и при перерегулировании не превышающем 10% (σ).

Таблица 1 — Данные качества регулирования при различных коэффициентах PID

№	P	I	D	t рег , с	σ, %	График
1.	0,5	0	1	8,5	15	—
2.	0,55	0	1	8,65	20	—
3.	0,45	0	1	5,85	8,75	Рисунок 8
4.	0,40	0	1	4,27	2,5	Рисунок 9
5.	0,36	0	1	5,1	0	Рисунок 10
6.	0,36	0	1,1	8,35	0	—
7.	0,36	0	0,9	6,25	6,25	—	0,40	0	1,1	7,5	0	Рисунок 11
9.	0,40	0	0,9	6,64	11,25	Рисунок 12
10.	0,40	0,1	1	11,5	63,75	Рисунок 13

Согласно данным из таблицы 1, наилучший результат регулирования при коэффициентах указанных в пункте 4. Результаты регулирования с коэффициентами из пунктов 3, 5, 8…10, являющихся точками в окрестности + 10% параметров из пункта 4, имеют худшие параметры регулирования.

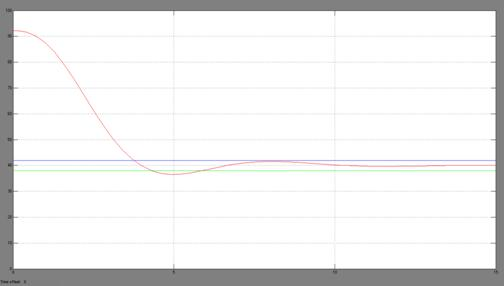
Рисунок 8 — График перерегулирования при P = 0,45; I = 0; D = 1

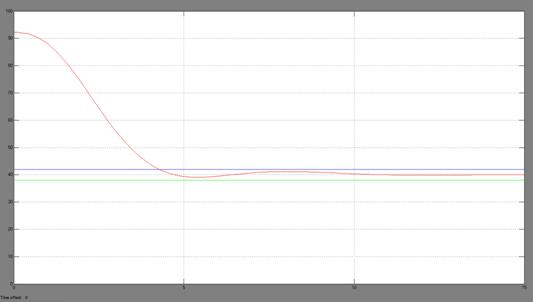
Рисунок 9 — График перерегулирования при P = 0,4; I = 0; D = 1

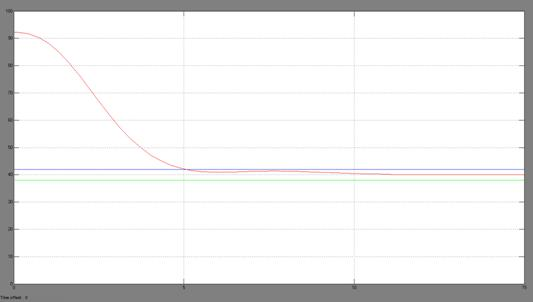
Рисунок 10 — График перерегулирования при P = 0,36; I = 0; D = 1

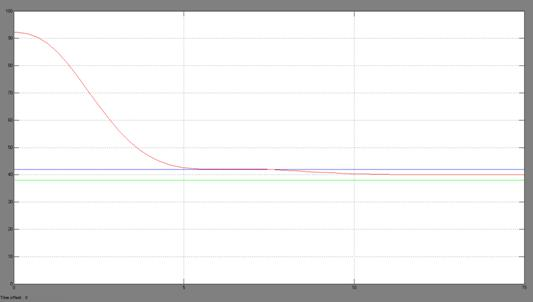
Рисунок 11 — График перерегулирования при P = 0,4; I = 0; D = 1,1

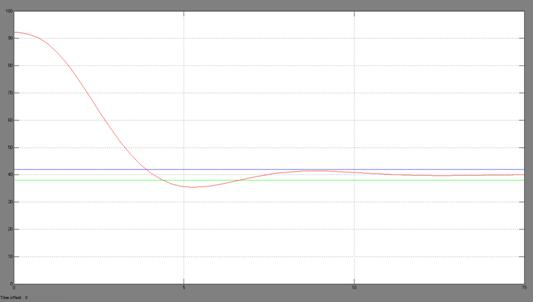
Рисунок 12 — График перерегулирования при P = 0,4; I = 0; D = 0,9

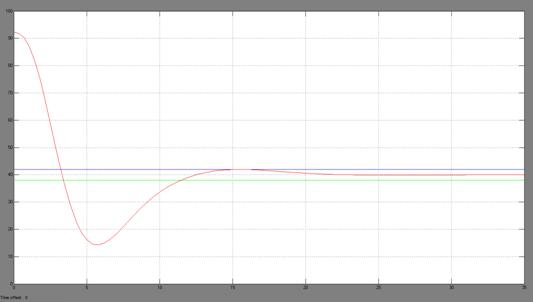
Рисунок 13 — График перерегулирования при P = 0,4; I = 0,1; D = 1

В результате проведенных исследований установлено, что:

) увеличение коэффициента пропорциональной части регулятора увеличивает колебания переходного процесса;

) введение дифференцирующего звена уменьшает перерегулирование и время регулирования, делает переходный процесс сходящимся;

) последовательное увеличение коэффициента дифференцирующего звена приводит к сокращению амплитуды колебаний;

) отсутствие статической ошибки можно объяснить наличием интегрирующего звена в цепи управления;

) приемлемым регулятором можно считать ПД-регулятор, так как введение интегрирующей составляющей делает САР неустойчивой (переходный процесс расходящийся);

6) приемлемыми параметрами настройки можно считать: P = 0,4; I = 0; D = 1, так как имеется допустимое перерегулирование, время регулирования минимально.

В ходе выполнения курсовой работы получены навыки разработки математических моделей систем автоматического регулирования и определения параметров настройки регуляторов на системе автоматического управления температурой жидкости на выходе теплообменника проточного типа. Разработана математическая модель системы автоматического управления температурой жидкости на выходе теплообменника проточного типа. При выполнении работы построена концептуальная, математическая и инструментальная модели объекта; модель исследована и определены оптимальные настройки регулятора.

1. Гороновский И.Т. Краткий справочник по химии [Текст] / И.Т. Гороновский и др. — Наукова думка, 2012. — 739 с.

2. Луценко В.А. Математическое моделирование химико-технологических процессов на аналоговых вычислительных машинах [Текст] / В.А. Луценко, Л.Н. Финякин 2-е изд. перераб. и доп. — М.: Химия, 2009.

. Демченко В.А. Автоматизация и моделирование технологических процессов АЭС и ТЭС [Текст] / В.А. Демченко — Одесса: Астропринт, 2011. — 305 с.

. Казаков А.В. Основы автоматики и автоматизации химических производств. Учебное пособие для ВУЗов [Текст] / А.В. Казаков, М.В. Кулаков, Ю.К. Мелюшев — М.: Машиностроение, 2010. — 376 с.