Система обработки информации содержит мультиплексный канал и ЭВМ. Сигналы от датчика поступают в канал через интервалы времени, распределённые по равномерному закону в диапазоне от 20 сек. до 40 сек. В канале они буферизуются и предварительно обрабатываются, ёмкость накопителя 10 величин сигналов. Обработка в ЭВМ осуществляется в течение интервала времени, распределенного по равномерному закону, в диапазоне от 15 до 45 сек.
Время безотказной работы и время восстановления ЭВМ распределены по закону Вейбулла-Гнеденко. Среднее значение времени безотказной работы 36 часов, параметр формы распределения 
= 0,95; среднее времени восстановления 20 мин, значение параметра формы распределения 
=0,85. Во время отказа ЭВМ обслуживание сигналов датчика прекращается; заявка, обслуживание которой было прервано, возвращается в начало очереди, время обслуживания обнуляется.
Разработать:
- Модели датчика информационных сигналов и времени обслуживания сигнала датчика в ЭВМ как генераторы последовательности случайных величин, методом обратной функции, с проверкой качества последовательности по гистограмме распределения.
- Модели генераторов последовательности случайных чисел, имитирующих время безотказной работы и время восстановления ЭВМ, с использованием метода Бусленко, с проверкой качества последовательности по гистограмме распределения.
- Смоделировать работу системы в течение времени, составляющего 15 дней. Определить вероятностно-статистические характеристики модели.
Поскольку функционирование данной вычислительной системы подразумевает поступление внешних сигналов от датчиков через случайные моменты времени, и продолжительность обработки данных на ЭВМ тоже не одинакова для всех сообщений, то для имитации этих процессов потребуются генераторы случайных чисел. Для задания времени безотказной работы ЭВМ и времени, требующегося на ее восстановление, также применяются генераторы случайных величин.
Из условия известно, что сигналы от датчиков поступают через интервалы времени, распределенные равномерно в диапазоне от 20 до 40 секунд. Генератор, служащий для имитации работы датчиков, назовем ГСЧ 1А. Обработка в ЭВМ осуществляется в течение интервала времени, распределенного по равномерному закону, в диапазоне от 15 до 45 сек. Генератор, применяемый для нахождения интервала времени, необходимого на обработку сигналов, назовем ГСЧ 1Б. Время безотказной работы ЭВМ, распределенное по закону Вейбулла-Гнеденко с параметром формы распределения β = 0,95 и максимальным значением 36 часов, будет имитировать генератор с названием ГСЧ 2А. Время восстановления ЭВМ, распределенное по этому же закону, но с параметром β = 0,85 и максимальным значением 20 минут, будет определяться генератором ГСЧ 2Б.
Курсовая работа автоматические системы
... системы или элемента, заключающееся в проведении восстановительных работ после появления отказа с целью восстановления работоспособности. Надежность – свойство системы ... закона распределения. Вид закона распределения выбирают ... системы или элемента). Отказ одного из элементов системы может привести к нарушению устойчивости, что представляет собой отказ системы. Для систем автоматического ... безотказная ...
2.1 ГСЧ 1А и ГСЧ1Б
Для разработки генератора последовательности случайных чисел, имитирующего сигналы от датчиков, применим метод обратной функции.
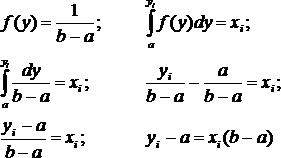
В итоге получим:
,
x i
y i
а подставив значения a = 15, b = 45 получим выражение для ГСЧ 1Б:
y i
На основании этих выражений напишем простейшие функции, реализующие работу данных генераторов:
/* Функция генерирует числа от 20 до 40, распределенные по равномерному закону (сигналы от датчиков) */
double GenRand1a()
{20.0 + 20.0 * (static_cast<double>(rand()) / RAND_MAX);
}
/* Функция генерирует числа от 15 до 45, распределенные по
равномерному закону (обработка в ЭВМ) */
double GenRand1b()
{15.0 + 30.0 * (static_cast<double>(rand()) / RAND_MAX);
}
.2 ГСЧ 2А и ГСЧ2Б
одинаковых по площади
После того, как будет выбран номер прямоугольника (интервала) с помощью генератора равномерно распределенных величин, мы получим интервал, на котором лежит генерируемое значение. Для его уточнения прибавим к левой границе этого интервала равномерно распределенное число от 0 до ширины интервала (прямоугольника).
a i
x i
Теперь рассмотрим, как описанный выше механизм работы генератора реализован в программе. Перед применением генератора необходимо произвести его инициализацию, которая как раз и подразумевает процесс разбиения промежутка генерации на равные по площади прямоугольники, этот процесс выполняется в функции Init().
void GenRand2::Init()
{pos = x1;sq = 0, sq1;
/* Вычислим площадь под графиком VeibulZakon() */
{+= VeibulZakon(pos) * step;+= step;
- } while (pos <
- x2);
- // Найдем единичную площадь, т. е. площадь одного прямоугольника
sq1 = sq / n;(granica != NULL)
{[] granica;= NULL;
- }= new double[n + 1];[0] = x1;
- = x1;
- int i;
/* Найдем границы интервалов, путем разделения всей имеющейся
площади по площадям отдельных прямоугольников */
Генератор случайных чисел
... получения случайных чисел называют генераторами случайных чисел (ГСЧ) или датчиками случайных чисел. Аппаратные ГСЧ ... случайных чисел, формируемых тем или иным ГСЧ, должны удовлетворять ряду требований. Во-первых, числа должны выбираться из определенного множества (чаще всего это действительные числа в интервале ... более сложных фигур, когда рассчитать площадь другим способом становится слишком сложно. ...
for (i = 1; i < n; i++)
{= 0;
- {+= VeibulZakon(pos) * step;+= step;
- } while (sq <
- sq1);[i] = pos;
}
Непосредственная генерация значений производится функцией Generate(), реализованной следующим образом:
double GenRand2::Generate()
{(!IsInit)
Init();interval;
/* Определяем номер требуемого интервала — это
случайное число от 0 до n — 1 */
interval = rand() % n;left_val, right_val;
/* Найдем правую и левую границы интервалов */
left_val = granica[interval];_val = granica[interval + 1];
- // Генерируем число на полученном интервалеvalue = (static_cast<double>(rand()) / RAND_MAX) *
(right_val — left_val) + left_val;
- return value;
}
Следует заметить, что процедура инициализации генератора требует больших затрат машинного времени, но последующая генерация значений осуществляется очень быстро. Разработанный класс применяется как для ГСЧ 2А, так и для ГСЧ 2Б, достаточно объявить соответствующие переменные с разными параметрами:
- Generator2a = new GenRand2(0.95, 36, 36, 42);b = new GenRand2(0.85, 20, 20, 27);
.3 Оценка качества ГСЧ
Проверку качества полученных генераторов будем проводить по гистограмме распределения: построим гистограмму распределения и вычислим площадь отклонений ее значений от идеальной гистограммы распределения для соответствующего закона.
Для этого сгенерируем последовательность псевдослучайных величин определенной длины, например из 3000 значений. Разобьем интервал от минимального до максимального генерируемого значения на некоторое количество интервалов равной ширины, например на 10. Распределим сгенерированные значения по принадлежности к тому интервалу, в котором они лежат. Подсчитаем количество значений, лежащих в каждом интервале, и на основе этих данных построим гистограмму. Ширина столбцов гистограммы будет равна
,
x 1
,
n i
.
Для идеальной гистограммы распределения равномерного закона высота и площадь столбцов будут одинаковыми и рассчитываются следующим образом:
.
Площадь столбов идеальной гистограммы для закона Вейбулла-Гнеденко будет определяться по формуле:
,
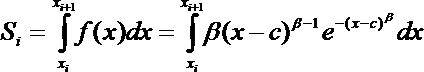где i — номер интервала, xi и xi + 1 — начало и конец i -го интервала.
Измерительные сигналы
... априорной информации переменные измерительные сигналы делятся на детерминированные, квазидетерминированные и случайные. Детерминированный сигнал - это сигнал, закон изменения которого известен, а модель не содержит неизвестных параметров. Мгновенные значения детерминированного сигнала известны в ...
Посчитаем по приведенным выше формулам площади столбцов для сгенерированной последовательности и для идеальной последовательности и рассчитаем площадь отклонений:
,
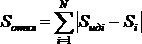S ид i
,
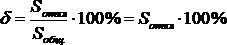S общ
Описанный алгоритм вычисления погрешности распределения реализован в программе, также имеется возможность построения гистограммы распределения. На рисунке Рисунок 1 показан расчет погрешности распределения для 10 интервалов разбиения и 3000 генерируемых значений для генератора ГСЧ 1А. На рисунке Рисунок 2 показан аналогичный расчет для ГСЧ 1Б. Как видно из этих рисунков, полученные значения погрешности распределения не превышают рекомендуемого значения для равномерного закона распределения, равного 5%. Это позволяет сделать вывод, что последовательности значений, получаемые генераторами ГСЧ 1А и ГСЧ 1Б, являются достаточно качественными. На рисунках Рисунок 3 и Рисунок 4 изображены гистограммы распределения для ГСЧ 1А и ГСЧ 1Б соответственно, построенные по сгенерированным значениям.
Расчет погрешности распределения для ГСЧ 2А показан на рисунке Рисунок 5, а на рисунке Рисунок 6 приведена гистограмма распределения, построенная на основе сгенерированных значений. Аналогичные сведения для ГСЧ 2Б приведены на рисунках Рисунок 7 и Рисунок 8. Как видно по гистограммам, столбцы, построенные по реально сгенерированным значениям, мало отличаются от идеальных. Это позволяет говорить о высоком качестве спроектированных генераторов.
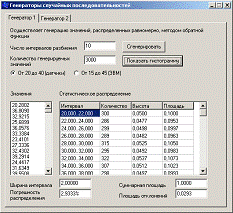
Рисунок 1
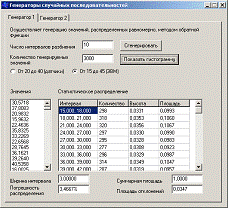
Рисунок 2
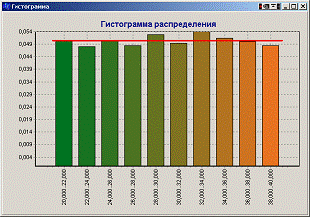
Рисунок 3
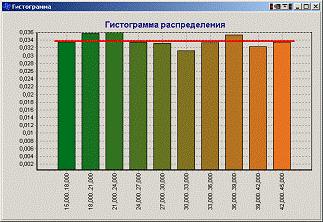
Рисунок 4
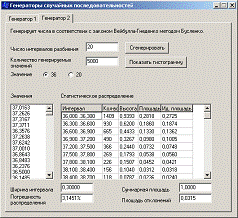
Рисунок 5
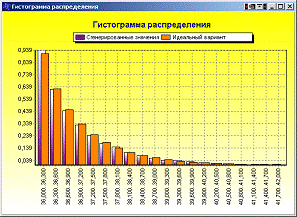
Рисунок 6
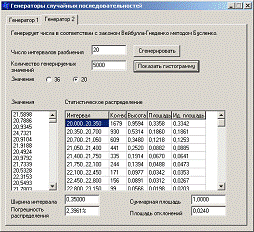
Рисунок 7
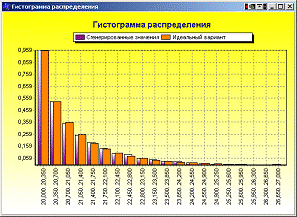
Рисунок 8
3.1 Разработка структурной схемы
Сообщения от датчиков сигналов поступают в канал, где они буферизируются и предварительно обрабатываются перед обработкой на ЭВМ. Если ЭВМ находится в активном состоянии (не сломана) и не занята обработкой, то она считывает сообщение из мультиплексного канала и приступает к его обработке. Если ЭВМ сломалась, и во время поломки обрабатывала сообщение, то обработка этой заявки прекращается, и она направляется обратно в канал, в начало очереди. В то время, когда ЭВМ находится на восстановлении, обработка сигналов не ведется. После восстановления ЭВМ обработка сигналов возобновляется.
Мультиплексный канал реализован по принципу очереди FIFO: первый зашел, первый вышел. Максимальное количество заявок, хранимое в мультиплексном канале, равно 10. Если канал полностью заполнен и поступают новые заявки, то старые заявки удаляются из конца очереди. Структурная схема модели изображена на рисунке
Генераторы измерительных сигналов
... схема генераторов низких и инфронизких частот, а также генераторы с фиксированным значением частоты входного сигнала. Обобщенная структурная схема формирования цифро-аналогового генератора и принцип кусочно-ступенчатой аппроксимации входного сигнала представлен на рисунках. Рисунок 5. ...
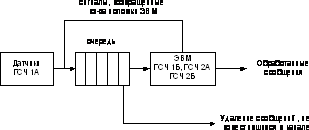
Рисунок 9
3.2 Расчет статистических показателей
В разрабатываемой программе будет вестись расчет статистических показателей эффективности моделируемой системы. Приведем формулы, применяемые для вычисления этих показателей.
Коэффициент готовности ЭВМ будет определяться как отношение времени нахождения ЭВМ в активном состоянии (когда она не сломана) ко времени работы системы:
.
Коэффициент загрузки ЭВМ найдем как отношение времени обработки сигналов на ЭВМ ко времени нахождения ЭВМ в активном состоянии (когда ЭВМ способна этим заниматься):
.
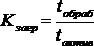Показатель эффективности будем рассчитывать путем деления количества обработанных сигналов, на количество сигналов, поступивших от датчика:
.
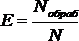.3 Разработка алгоритмической модели
На основании структурной схемы построим алгоритмическую модель вычислительной системы, она показана на рисунке Рисунок 10. Особенностью подхода при проектировании алгоритмической модели является использование объектно-ориентированного программирования, т. е. датчик, мультиплексный канал и ЭВМ представлены в виде объектов, которые взаимодействуют между собой. Это позволяет существенно упростить понимание имитационной модели, поскольку достигается высокий уровень абстрагирования. А все особенности работы скрыты внутри реализации классов. Не погружаясь в техники программирования, можно понять работу этой модели.
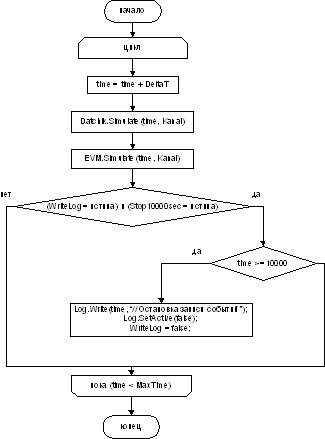
Рисунок 10, Генераторы,, Вести запись событий
Когда будут выбраны необходимые опции, можно запустить процесс моделирования, для этого нужно нажать на кнопку Запуск . После завершения процесса моделирования на экране появится информация о модели и рассчитанные статистические показатели. На рисунке Рисунок 11 показан пример работы программы.
