Гараж в городе Омске расположен во втором климатическом районе, кратковременная нагрузка от снегового покрова равна 700 Н/м, а длительная равна нулю. В знании два этажа. Пролет здания равен 6 м, шаг колонн равен 6,3м, высота этажа 4м, глубина заложения фундамента 1,5м, ширина панели равна 1,6м.
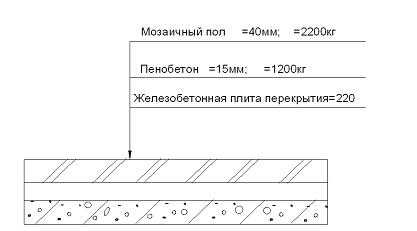
Рисунок 1.1 Узел конструкции перекрытия

Рисунок 1.2 Узел конструкции покрытия
2. Расчет железобетонной плиты перекрытия
Задание для проектирования. Расчет железобетонной плиты перекрытия. Требуется рассчитать и сконструировать сборную железобетонную плиту перекрытия гаража в городе Омске при следующих данных: пролет здания 6,0м., временная нагрузка на перекрытие рncd=1500Н/м2, ширина плиты 1,6м., номинальная длина панели 6,3м. Действующие на перекрытие нагрузки указаны в табл.2.1.
Таблица 2.1 Сбор нагрузок на междуэтажные перекрытия
|
Вид нагрузки |
Нормативная нагрузка, Н/м2 |
Коэффициент надежности по нагрузке,гf |
Расчетная нагрузка, Н/м2 |
|
Постоянная: — мозаичный пол д=40мм.г=2000кг/м3 0,04∙20000= — пенобетон д=15мм.г=1200кг/м3 0,015∙12000= — железобетонная плита перекрытия |
880 180 2750 |
1,3 1,2 1,1 |
1144 216 3025 |
|
Итого: Временная: — кратковременная — длительная |
gn=3810 рncd =1500 — |
1.3 — |
g=4385 рcd =1950 — |
|
Итого: |
pn=1500 |
— |
p=1950 |
Определение нагрузок и усилий. Определяем нагрузку на погонный метр плиты при ширине 1,6м:
Кратковременная нормативная рncd =1500 * 1,6=2400 Н/м2
Кратковременная расчетная рcd =1950*1,6=3120 Н/м2
Постоянная и длительная нормативная
рnld+ gn=(0+3810)*1,6=6096 Н/м2
Постоянная и длительная расчетная
рld + g=(0+4385)*1,6=7016 Н/м2
qn=(рnld+ gn + рncd)1.6=(0+3810+2400)*1.6=9936 Н/м2
q=(рld+ g + рcd)1.6=(0+4385+3120)1.6=12008 Н/м2
Определяем расчетную длину плиты
l0=ln-b1/ 2 -b2/ 2=6,3-0.2/2-0.1/2=6,15м
где ln=6,3м.,номинальная длина плиты;
b1=0,2м.,опирание плиты на кирпичную стену;
b2=0,1м.,опирание плиты на железобетонную стену.
Расчетный изгибающий момент по полной нагрузки
М=q∙l02∙гn / 8=12008∙6,152∙0,95/8=53932,9 H∙м
q=12008Н/м2, полная расчетная нагрузка;
l0=6,15м.,расчетная длина плиты;
гn=0,95, коэффициент надежности по назначению конструкции.
Максимальная поперечная сила на опоре от расчетной нагрузки
Q= q∙l0∙гn /2=12008∙6,15∙0,95/2=35078,37 H
Подбор сечения. Для изготовления сборной панели принимаем: бетон класса В30, Еb=32500МПа, Rb=17МПа, Rbt=1.2МПа, гb2=0.9;продольную арматуру — из стали класса А-II, Rs=280МПа,поперечную арматуру — из стали класса А-I, Rs=225МПа и Rsw=175МПа; армирование- сварными сетками и каркасами; сварные сетки в верхней и нижней полках панели- из проволоки класса Вр-I, Rs=360МПа при d=5мм и Rs=365МПа при d=4мм.
Определяем высоту сечения
h=c∙l0∙ Rs/Es∙ и ( gn+ рnld)/qn=18∙615∙280/2.1∙105 * 2(3810+0)/5310=26см
где с=18-20для пустотных, коэффициент определяющий конструкцию плит;
l0=615см,расчетная длина;
Rs=280МПа,расчетное сопротивление материала;
Es=2,1∙105МПа
и=2 для пустотных, коэффициент учитывающий прогиб при длительной нагрузке;
gn+ рnld =3810 Н/м2, нормативная постоянная и длительная нагрузка;
qn =5510 Н/м2, полная расчетная нагрузка.
В расчете поперечное сечение пустотной панели приводим к тавровому сечению.
Необходимо преобразовать круглые пустоты в квадратные с равными площадями и с одинаковыми моментами инерции. Сторона квадрата
h1=d/2∙√р=0.9d=0,9∙200=180мм
d=180мм,диаметр пустоты.
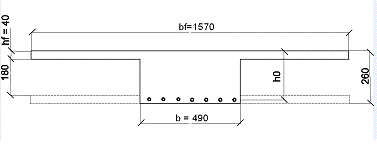
Рисунок 2.1 — Приведенное расчетное поперечное сечение.
Нижней полкой в расчете плиты пренебрегаем, т.к. она не работает.
Расчет по прочности нормальных сечений. Предварительно определяем положение нейтральной оси:
Если hf`/h>0.1,то нейтральная ось проходит в полке;
hf`/h<0.1,то нейтральная ось проходит в ребре.
hf`/h=40/260=0,154>0.1 ,
рассчитываем как прямоугольное сечение шириной bf`=157см.
Рабочая высота сечения
h0=h-a=26-3=23cм
определяем коэффициент оптимального армирования
A0=M/Rb∙гb2∙bf`∙h02=5393290/17(100)∙0.9∙157∙529=0.042
M=53932,2 Н*м, расчетный изгибающий момент;
Rb=17 МПа, расчетное сопротивление бетона сжатию;
гb2=0,9, коэффициент условий работы бетона;
bf`=1570 мм, ширина полки;
h0=230 мм, рабочая высота.
методом интерполяции:
|
о |
A0 |
з |
|
0,04 0,043 0,05 |
0,039 0,042 0,048 |
0,98 0,9783 0,975 |
Высота сжатой зоны
х=о∙h0=0,043∙23=0,989см< hf`=4 cм,
нейтральная ось проходит в пределах сжатой полки.
Определяем площадь рабочей арматуры
Аs=M/з∙Rs∙h0=5393290/0.9783∙280(100)∙23=8.56 см2
Предварительно принимаем количество и диаметр рабочей арматуры
Ø14 А-II(Аs=10.77 см2),а также учитывая сетку С-I
![]()
5 Ø5 Вр-1Аs1=1.57см2;
∑Аs= Аs+ Аs1=10.77+1.57=12.34 см4.
Расчет плиты по наклонному сечению
Проверяем условие необходимости постановки поперечной арматуры для многопустотных панелей, максимальная поперечная сила Qmax=35078.37 Н
Вычисляем проекцию с наклонного сечения по формуле
с=цb2(1+цf+цn)∙Rbt∙b∙ h02/Qb=Вb/ Qb
цb2=2,для тяжелого бетона;
цn=0, коэффициент учитывающий предварительное напряжение для ненапрягаемой плиты;
цf- коэффициент учитывающий свесы сжатых полок; в многопустотной плите при пяти ребрах
цf=nр∙0,75∙(3hf`)hf`/bh0=7∙0,75∙(3∙ 4)4/49∙23=0,22≤0.5
Исходя из условий равновесия Qsw=Q
Из условия предельного состояния
Qсеч=Qsw+Qb=Q
В расчетном наклонном сечении
Qb=Qsw=Q/2=17539,185Н,
следовательно подставляем в формулу и определяем проекции наклонного сечения
с=цb2(1+цf+цn)∙Rbt∙b∙ h02/Qb
c=2(1+0.22+0)1.2∙49∙529(100)/17539,185=432,7>46см=2ho,
где если с>2ho принимаем с=2ho,
с<2hoпринимаем с=с.
Следовательно с=49см.
Определяем поперечную силу воспринимаемую сечением
Qb=цb2(1+цf+цn)∙Rbt∙b∙h02/с=2(1+0.22+0)1.2∙49∙212(100)/46=164992,8Н
Где если Qb>Q, то поперечная арматура по расчету не требуется
Qb<Q — требуется расчет арматуры
Следовательно Qb=164992,8 Н> Q =35078,37 Н — расчет не требуется.
Поперечную арматуру предусматриваем из конструктивных условий, располагая шагом
s≤h/2=26/2=13cм, а также s≤15см.
Назначаем поперечные стержни из условий сварки диаметром 4 мм класса А-I через 13см у опор на участках длиной ¼ пролета. В средней ½ части панели для связи продольных стержней каркаса по конструктивным соображениям ставим поперечные стержни через 19,5см, так как s<3h/4=3∙26/4=19,5см, а также s≤50см.
Определение прогибов. Момент в середине пролета от полной нормативной нагрузки
n=qn∙l02∙гn/8=9936∙6,152∙0.95/8=44626.77 H∙м
qn=9936 Н/м2, полная нормативная нагрузка;
l0=6,15 м., расчетная длина плиты;
гn=0.95, коэффициент надежности по назначению конструкции.
Момент от постоянной и длительной нагрузки
Мld=qldn∙l02∙гn/8=6096∙6,152∙0.95/8=27379.7 H∙м
qldn=6096Н/м2, нормативная постоянная и длительная нагрузка.
Момент от кратковременной нагрузки
Мcd=qcdn∙l02∙гn/8=2400∙6,152∙0.95/8=10779.4 H∙м
qcdn=2400 Н/м2, нормативная кратковременная нагрузка.
Прогиб f при изгибе свободно опертого элемента находят по кривизне 1/r в наиболее нагруженном сечении
f=Splo2∙1/r
где Sp=5/48, коэффициент учитывающий вид нагрузки и схему загружения: для свободно опертой балки, равномерно загруженной (таб.2.16,Мандриков) 1/r-кривизна плиты.
Кривизна в середине пролета панели, определяется по формуле
1/r=1/Es As ho2∙(Мld — k2ld b h2 Rbt.ser / k1ld)
Es=2.1∙105МПа, модуль упругости стали;
As=12.34 см2, площадь рабочих стержней и продольных стержней сетки; ho=23см, рабочая высота сечения;
Мld=27379.7 H∙м, момент от постоянной и длительной нагрузки;
b=49 см, ширина ребра;
h=26 cм, высота сечения;
Rbt.ser=1,8МПа, расчетное сопротивление бетона для предельных состояний второй группы;
Коэффициенты k1ld и k2ld определяем исходя из таб.2.19,Мандриков.
г’=(bf’-b)hf’ /bho=(157-49)4/49∙23=0,38
где bf’=157см, ширина полки;
b=49 см, ширина ребра;
hо=23 cм, рабочая высота сечения;
hf’=4см, высота полки;
мб=(As/ bho)∙Es/Eb=(10.77/49∙23)2.1∙105/32.5∙103=0.062
м- коэффициент армирования
As=10.77 см2,площадь рабочей арматуры;
Es=2.1∙105МПа, модуль упругости стали;
Eb=32.5∙103МПа, модуль упругости бетона.
Определяем коэффициенты k1ld =0,46 и k2ld=0,11
/r=(1∙2737970-0,11∙49∙262∙180)/210000(100)10.77∙232∙0,46= 0,000038
Вычисляем прогиб следующим образом
f=(5/48)6152∙0.000038=1,5см,
что меньше [ f ]=3см для элементов перекрытий с плоским потолком при l=6-7.5м из таб.2.2,Мандриков.
f=1.5см<3см=[ f ]- условие соблюдается расчетный прогиб меньше допустимого.
Расчет панели по раскрытию трещин. Панель перекрытия, согласно таблице 2.8, относится к третьей категории трещиностойкости как элемент, эксплуатируемый в закрытом помещении и армированный стержнями из стали А-II. Предельно допустимая ширина раскрытия трещин аcrc1=0.4мм и аcrc2=0,3мм.
Величину раскрытия трещин, нормальных к продольной оси элемента, определяют с учетом влияния ряда факторов по эмпирической формуле
аcrc=д∙цl∙з(уs/Es)20(3.5-100м) 3√d∙ дa
где д=1, коэффициент зависящий от вида воздействия, принимаемый равным 1 для изгибаемых и внецентренно сжатых элементов и 1,2 для растянутых;
цl- коэффициент учитывающий виды нагрузок, для кратковременной равен 1 ; для длительной и постоянной равен 1,6-15м
м=As/ bho=10.77/49∙23=0,0096, тогда цl=1,6-15∙0,0096=1,456;
з=1, коэффициент зависящий от вида и профиля продольной арматуры, при стержневой арматуре периодического профиля;
уs-нормальное напряжение в рабочей арматуре;
Es=2.1∙105МПа, модуль упругости стали;
d=14мм, диаметр рабочего стержня;
дa=1, коэффициент зависящий от защитного слоя бетона, если расстояние от центра тяжести сечения стержней крайнего ряда арматуры до наиболее растянутого волокна бетона а2≤0.2h=0,2∙26=5.2 см, то принимаем дa=1;
уs=М/Аsz1=M/Ws.
Ws-площадь арматуры на плечо внутренней пары.
Определяем z1:
z1=h0[1-(ц’f∙h’f/h+о2)/2(ц’f+о)],
здесь hо=23cм, рабочая высота сечения;
hf’=4 см, высота полки;
h’f/h=4/26=0,154;
ц’f- коэффициент изгиба:
ц’f =(bf’-b)hf’+бAs’/(2v) /bho =(1570-490)40/490∙230=0,38;
где bf’=157см, ширина полки;
b=49 см, ширина ребра;
hо=23cм, рабочая высота сечения;
hf’=40 см, высота полки;
бAs’/(2v)=0, для двойной арматуры.
по формуле находим о-относительная высота сжатой зоны:
о=1/[1,8+(1+5(д+л))/10мб
мб=(As/ bho)∙Es/Eb=(10.77/49∙23)2.1∙105/32.5∙103=0.062
л=ц’f[1-h’f /(2ho)]=0.38[1-4/(2∙23)]=0.347
Значение д от действия всей нормативной нагрузки:
д=Mn/Rb,serbho2=4462677/22(100)157∙232=0.024;
то же, от постоянной и длительной нагрузки:
дld=Mld / Rb,serbho2=2737970/22(100)257∙232=0.015
Вычисляем о при кратковременном действии всей нагрузки:
о=1/[1,8+(1+5(0,024+0,0347))/10∙0,062=0,185>0.154= h’f/h;
продолжаем расчет как тавровых сечений.
Значение z1 формуле
z1=h0[1-(ц’f∙h’f/h+о2)/2(ц’f+о)]=23[1-(0,38∙0,154+0,1862)/2(0,38+0,186)] =21.108см
Упругопластический момент сопротивления железобетонного таврового сечения после образования трещин
Ws=Asz1=10.77∙21.108=227.3см2.
Расчет по длительному раскрытию трещин. Мld=27,3797кН∙м. Напряжение в растянутой арматуре при действии постоянных и длительных нагрузок
уs2=Mld/Ws=27379870/227.3=12042.99Н/см2=120.43МПа
Ширина раскрытия трещин от действия постоянной и длительной нагрузок при цl=1.456
аcrc2=1∙1,456∙1(120.43/2,1∙105)20(3.5-100∙0,0096)3√14∙1= =0,1022мм<аcrc,max=0,3мм;
условие удовлетворяется.
Расчет по кратковременному раскрытию трещин. Mn=44626.77 H∙м. напряжение в растянутой арматуре при совместном действии всех нормативных нагрузок
уs1=Mn/Ws=44626.77/227.3=19633.42Н/см2=196.33 МПа
Приращение напряжения от кратковременного увеличения нагрузки от длительно действующей до её полной величины
∆уs=уs1-уs2=196.33-120.43=78.9 МПа.
Соответствующее приращение ширины раскрытия трещин при цl=1 будет:
∆аcrc=acrc1-acrc2=1∙1∙1(75.9/2,1∙105)20(3.5-100∙0,0096) 3√14∙1=0,044мм.
Ширина раскрытия трещин при совместном действии нагрузок
acrc=0,1022+0,044=0,15мм< аcrc1,max=0,4мм,
условие соблюдается.
Проверка панели на монтажные нагрузки. Панель имеет четыре монтажные петли из стали класса А-I, расположенные в крайних рёбрах на расстоянии 0,7 м от концов панели. С учетом коэффициента динамичности kd=1,4 расчетная нагрузка от собственного веса панели
q=kd∙гf∙gn∙b=1,4∙1,1∙2750∙1.57=6648.95Н/м,
где гf=1,1, коэффициент надежности по нагрузке;
gn=2750Н/м2, постоянная нормативная нагрузка;
b=1.57 м, конструктивная ширина панели.
Определяем изгибающий момент консольной части панели
М=q∙l12/2=6648.95∙0.72/2=1628.99Н∙м.
Этот момент воспринимается продольной монтажной арматурой каркасов. Полагая, что z1=0.9ho,требуемая площадь сечения указанной арматуры составляет
As=M/z1∙Rs=162899/0.9∙23∙280(100)=0.28см2,
что значительно меньше принятой конструктивно арматуры 7Ø 10 А-II, Аs=5.5 см2.
При подъёме панели вес её может быть передан на две петли. Тогда усилие на одну петлю составляет
N=q∙l/2=6648.95∙6,290/2=20910.95H.
Площадь сечения арматуры петли
Аs=N/Rs=20910.95/[210(100)]=0.9958cм2;
Принимаем конструктивно стержни диаметром 12мм, Аs=1.131 см2
.2 Расчет сборного железобетонного марша
Рассчитать и сконструировать железобетонный марш шириной 1,5 м для двухэтажного гаража в городе Омске. Высота этажа 4,0 м. Угол наклона марша б ≈ 30º, ступени размером 15×30 см. Бетон класса В25; Rb = 14,5 МПа; Rbt =1.05 МПа; гb2 = 0.9,Rb,ser = 18.5 МПа; Rbt,ser = 1,6 МПа; Еb=27000 МПа; арматура класса А-II; Rs = 280 МПа; Rsw =215МПа, для проволочной арматуры класса А-II, сетки из проволоки класса Вр-1.
Определение нагрузок и усилий.
Определяем количество ступенек: 4/0,15=26,5=27, один марш составляет 14 ступенек. Длина лестницы l=300*14=4200 мм
l1=l/cosб=4200/0.866=4850мм
Собственный вес типовых маршей по каталогу индустриальных изделий для жилищного и гражданского строительства (ИИ-03) составляет q = 3,6 КН/м² горизонтальной проекции.
По данным в таблице 2.3 (стр73) (Мандриков) пункт 11(по пункту10) определяем кратковременная нормативная рncd =4000 Н/м,
длительная нормативная рnld=1400Н/м,
рn=5400 Н/м
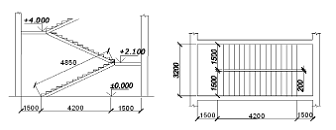
Рисунок 2.2.1 — Расчетная схема марша
Длина марша в горизонтальной проекции составляет l =4,2 м, а длина под углом б=30º определяется по формуле:
l1 = l / cosб =4200/0,866 = 4850 мм
Расчетная нагрузка на 1 м длины марша
q = (gn гf + pn гf)a,
где a — ширина марша
q = (3,5*1,1+5,4*1,2)*1,5 = 13,68 кН/м
Расчетный изгибающий момент в середине пролета марша
М = ql²/8cosб = 13,68*4,2²/8*0,866 = 34,8 кН·м
Поперечная сила на опоре
Q = ql /2cosб = 13,68*4,2 /2*0,866 = 33,17 кН
Предварительное назначение размеров сечения марша. Применительно к типовым заводским формам назначаем толщину плиты (по сечению между ступенями) h`f = 30 мм, высоту ребер h = 170 мм, толщину ребер br = 80 мм
Действительное сечение марша заменяем на расчетное тавровое с полкой в сжатой зоне b = 2br = 2*80 = 160 мм; ширину полки b`f при отсутствии поперечных ребер принимаем не более
b`f = 2(l / 6) + b = 2(420/6)+16 = 156 см или b`f = 12h`f+b = 12*3+16 = 52 см, принимаем за расчетное меньшее значение b`f = 52 см
а
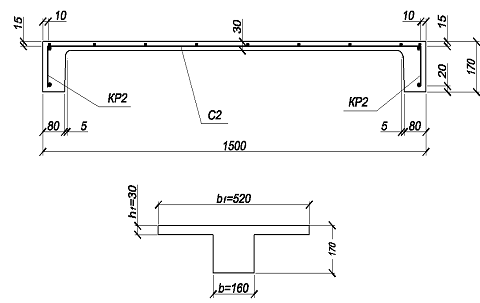
b
Рисунок 2.2.2 — Поперечные сечения
а) фактическое
b) приведенное
Подбор площади сечения продольной арматуры. Устанавливаем расчетный случай для таврового сечения (при х = h`f): при М≥Rbгb2b´fh`f (ho-0,5h`f) нейтральная ось пересекает ребро;
>14,5(100)*0,9*52*3(14,5-0,5*3) = 2646540 Н·см;
Вычисляем:
Находим момент, воспринимаемый свесами сжатой полки:
Мсв=Rb ( bf -b)hf (h0-0,5hf)=14,5* 102 (52-16) 3 ( 14,5-0,5 3)=
=2035800 Н м
Определяем площадь соответствующей растянутой арматуры, воспринимающей этот же момент:
AS св=Мсв/ RS(h0 -0,5hf)= 2035800/ 280* 100 ( 14,5 -0,5 *3)= 5,59 см2
Вычислим момент, воспринимаемый ребром:
М1= М — Мсв=34800 — 20358= 14442 н м
Определяем коэффициент оптимального армирования:
А0=М1 /Rb b h02 = 1444200/ 14,5 100 16 14,52 = 0,295< A0max=0,43
следовательно сжатая арматура не нужна.
По таблице 2.12 (Мандриков) находим з=0,0,82
Определяем площадь рабочей арматуры, работающей совместно с ребром:
AS1=M1 / RS h0 з=1444200 / 280(100) 14,5 0,82=4,34 см2
Находим полное сечение растянутой арматуры:
AS=ASсв + AS1=5,59 + 4,34=9,93 см2
Принимаем 2 ǿ 28 АII (AS=12,32 см2)
Расчет наклонного сечения на поперечную силу. Поперечная сила на опоре Qmax = 33,17*1 = 33,17 кН. Вычисляем проекцию расчетного наклонного сечения на продольную ось с по формуле:
цb2(1+ц f +ц n)Rbt гb2 b ho² ,
где цn = 0;
цf = 2(0,75(3hґf)hґf)/bho = 2(0,75*3*3²/16*14,5)= 0,175 <0,5;
(1+цf + цn) = 1+0,175+0 = 1,175 < 1,5
цb2(1+ц f +ц n)Rbt гb2 b ho² = 2*1,175*1,05*0,9(100)16*14,5² = 718601Н/см;
В расчетном наклонном сечении Qb=Qsw=Q/2, следовательно подставляем в формулу и определяем проекции наклонного сечения
с=цb2(1+цf+цn)∙Rbt∙b∙ h02/Qb<2ho
c=2(1+0.175+0)1.05∙16∙14,52(100)/0,5*33170=50,1 см>29см=2ho,
где если с>2ho принимаем с=2ho,
с<2ho принимаем с=с.
Следовательно с=29см.
Определяем поперечную силу воспринимаемую сечением
=цb2(1+цf+цn)∙Rbt∙b∙h02/с=2(1+0.175+0)1.05∙16∙14,52(100)/29=28623Н
Где если Qb>Q, то поперечная арматура по расчету не требуется
Qb<Q — требуется расчет арматуры
Следовательно 28623 Н<33170 Н-требуется расчет арматуры.
Исходя из условий сварки , по диаметру продольной рабочей арматуры, равному 28 мм, определяем наименьший диаметр поперечных стержней, равный 8 мм (по таблице 3 приложение II Мандриков).
Площадь сечения одного поперечного стержня ( по таблице 1 приложение II Мандриков)
ASW=0,503 см2. Число каркасов по ширине сечения балки n=2
Определяем предельное усилие, воспринимаемое поперечными стержнями:
qSW=(Q/2)2/(цb2 Rbt b h02)=(33170/2)2/(2 1,05 100 0,9 16 14,52)=389 н/см
где цb2=2-для тяжелого бетона.
Усилия в хомутах учитываются на длине проекции наклонной трещины с0, которая не должна превышать 2h0.
с0= ![]() цb2 Rbt b h0 /qSW=
цb2 Rbt b h0 /qSW=![]() 2 1,05 0,9 100 16 14,52/389=40.43 см
2 1,05 0,9 100 16 14,52/389=40.43 см
Уточняем qSW, исходя из условия:
если с0<2h0,, то qSW=Q/c0 — цb2 Rbt b h02/c02
если с0>2h0 , то qSW=Q/(2h0)-цb2 Rbt b h02/(2h0 c0 )
Так как с0.=40.43 см >2h0,=2 14,5=29 см,
qSW=Q/(2h0)-2Rbt гb2 b h0/2h0 c0=33170/29-2 1,05 100 0,9 16 14,52/
/2 14,5 112,62 =942,12н/см
где гb2-коэффициент условий работы бетона (таблица 1.5 Мандриков)
Определяем шаг поперечных стержней :
s=RSW n ASW /qSW1=215 2 0,503 /942,15=22,8 см
где АSW1- площадь сечения одного поперечного стержня
Наибольший шаг:
=0,75 цb2 Rbt гb2 b h02/Q=0,75 2 1,05 100 0,9 16 14,52/33170=14,38 см
Кроме того, согласно конструктивным требованиям на приопорных участках, равных 1/4 пролёта, при высоте сечения балки h<45 см, шаг поперечных стержней принимается не более h/2 и не более 15 см; Принимаем для приопорных участков s=17/2=8,5=9см, как наименьшее из всех значений s.
Вычисляем площадь сечения поперечной арматуры в расчетном сечении:
ASW=n ASW1=2 0,503=1,006 см2
Условие прочности бетона:
<0,3 цW1 цb1 Rb гb2 b h0
где цw1-коэффициент, учитывающий влияние хомутов, нормальных к продольной оси элемента; цw1=1+5бмw, где
б=Еs/Eb=210000/27000=7,78; мw=ASW/(b s)=1,006/(16 9)=0,007
цw1=1+7,78 0,007=1,27<1,3; цb1=1-в Rb,где в=0,01-для тяжелого бетона.
цb1=1-0,01 14,5=0,855
гb2=0,9-коэффициент условий работы бетона (таблица 1.5 Мандриков)
Проверяем условие прочности. Поперечная сила, воспринимаемая сечением:
Qсеч=0,3 1,27 0,855 14,5 100 0,9 25 57=98625,6 н >33170 н =
Условие прочности соблюдается.
Принимаем поперечные стержни диаметром 8 мм, шаг стержней в приопорных участках 80 мм, шаг в середине пролета 120 мм.
Определение прогибов. Момент в середине пролета от полной нормативной нагрузки
=qn∙l02∙гn/8cosб=8105∙4,2∙0,95/8*0,866=19605 H∙м
qn=8105Н/м2, полная нормативная нагрузка;
l0=4,2 м., расчетная длина марша;
гn=0,95, коэффициент надежности по назначению конструкции.
Момент от постоянной и длительной нагрузки
Мld=qldn∙l02∙гn/8cosб=5000*1,5∙4,22∙0,95/8*0,866=18142 H∙м
qldn=4000Н/м2, нормативная постоянная и длительная нагрузка.
Момент от кратковременной нагрузки
Мcd=qcdn∙l02∙гn/8cosб=4000*1,5∙4,2 2∙0,95/8*0.866=14513 H∙м
qcdn=4000Н/м2, нормативная кратковременная нагрузка.
Прогиб f при изгибе свободно опертого элемента находят по кривизне 1/r в наиболее нагруженном сечении
f=Splo2∙1/r
где Sp=5/48, коэффициент учитывающий вид нагрузки и схему загружения: для свободно опертой балки, равномерно загруженной (таб.2.16,Мандриков)
/r-кривизна плиты.
Кривизна в середине пролета панели, определяется по формуле
1/r=1/Es As ho2∙(Мld — k2ld b h2 Rbt.se r/k1ld)
Es=2.1∙105МПа, модуль упругости стали;
As=12,32 см2,площадь арматуры;
ho=14,5см, рабочая высота сечения;
Мld=18142H∙м, момент от постоянной и длительной нагрузки;
b=16см, ширина ребра;
Rbt.ser=1,6МПа,расчетное сопротивление бетона для предельных состояний второй группы;
Коэффициенты k1ld и k2ld определяем исходя из таб.2.19,Мандриков.
г’=(bf’-b)hf’+бAs’/(2v) /bho=(520-160)30/60∙130=0,519
где bf’=52см,ширина полки;
b=16см, ширина ребра;
hf’=3см, высота полки;
бAs’/(2v)=0, для двойной арматуры.
мб=(As/ bho)∙Es/Eb=(13,32/16∙13)2.1∙105/2,7∙104=0,41
м- коэффициент армирования
As=12,32 см2,площадь рабочей арматуры;
Es=2.1∙105МПа, модуль упругости стали;
Eb=2,7∙104МПа, модуль упругости бетона.
Определяем коэффициенты k1ld =0,23и k2ld=0
Вычисляем кривизну плиты:
/r=18142-0/210000*12,32*14,52=0,00003
Вычисляем прогиб следующим образом
f=(5/48)4202∙0,00003=0,551 см,
что меньше [ f ]=l/300см для элементов лестниц при пролетах l≤5м из таб.2.2,Мандриков.
F=0,551см<1,4см=[ f ]- условие соблюдается расчетный прогиб меньше допустимого.
Решение. Определение нагрузок. Собственный нормативный вес плиты при hf´=6cм; gn=0.06·25000=1500Н/м2; при подсчете расчетных нагрузок коэффициент надежности по нагрузке гf=1,1;расчетный вес плиты g=1500·1.1=1650Н/м2.
Площадь лобового ребра:
Sлр =0.3*((0,1+0,12)/2)+0.07((0,07+0,14)/2)=0,04035 м2
Нормативный вес одного погонного метра лобового ребра:
Gлрп= Sлр +1+gж/б=0,04035*1*25000=1009 Н/м2
Расчетный вес лобового ребра:
Gлр= Gлрп*1,1=1009*1,1=1110 Н/м2
Площадь крайнего ребра:
Sкр=((0,08+0,1)/2)*14=0,0126 м2
Нормативный вес одного погонного метра пристенного ребра:
Gкрп=0,0126*1*25000=315 Н/м2
Gкр=315*1,1=347 Н/м2
При расчете площадочной плиты рассматривают раздельно полку, упруго заделанную в ребрах, лобовое ребро, на которое опираются марши, и пристенное ребро, воспринимающее нагрузку от половины пролета полки плиты.
Расчет полки плиты. Полку плиты при отсутствии поперечных ребер рассчитывают как балочный элемент с частичным защемлением на опорах.
Расчетный пролет равен расстоянию между ребрами
lo= 1500-120-100=1280мм.
Изгибающий момент в пролете и на опоре определяют по формуле, учитывающей выравнивание моментов
М=q·lo2/16=7050·1,282/16=722Н·м
Где q=(g+p)b=(1650+5400)·1=7050Н/м2; b=1м.
При b=100см и hо=h-a=6-2=4cм вычисляем
A0=M∙гn/Rb∙гb2∙b∙h02=72200∙1/14.5(100)∙0.9∙100∙42=0.035
Rb=14.5МПа,расчетное сопротивление бетона сжатию;
гb2=0,9, коэффициент условий работы бетона;
b=100cм, ширина полки;
h0=4cм, рабочая высота.
методом интерполяции
|
о |
A0 |
з |
|
0,03 0,036 0,04 |
0,03 0,035 0,039 |
0,985 0,9822 0,98 |
Определяем площадь рабочей арматуры
Аs=M∙гn/з∙Rs∙h0=72200∙1/0.9822∙375(100)∙4=0,49см2
Укладываем сетку С-1 из арматуры Ø4мм Вр-І шагом s=200мм на 1м длины с отгибом на опорах , As=0,754см2
Расчет лобового ребра. На лобовое ребро действуют следующие нагрузки: постоянная и временная, равномерно распределенные от половины пролета полки и от собственного веса:
q = (1650+5400)*1,5/2+1110 =6398 Н/м;
равномерно распределенная нагрузка от опорной реакции маршей, приложенная на выступ лобового ребра и вызывающая его изгиб:
q1 = Q/a = 3317/1,5 = 2211 Н/м.
Изгибающий момент на выступе от нагрузки q на 1м:
M1 = q1((10+7)/2) = 2211*8,5 = 18793,5 Н см = 188 Н м
Определяем расчетный изгибающий момент в середине пролета ребра:
= (q+q1)l² гn/8 = (6398+2211)*3,2²/8 = 11020 Н м.
Расчетное значение поперечной силы с учетом гn = 1:
Q = (q+q1)l гn/2 = (6398+2211)*3,2*0,95/2 = 3271 H.
Расчетное сечение лобового ребра является тавровым с полкой в сжатой зоне шириной
b´f = 6h´f + br = 6*6 + 14 = 50см.
Так как ребро монолитно связано с полкой, способствующей восприятию момента от консольного выступа, то расчет лобового ребра можно выполнять на действие только изгибающего момента
М = 11020 Н м
В соответствии с общим порядком расчета изгибаемых элементов определяем (с учетом коэффициента надежности гn = 1) расположение нейтральной оси при х = h´f
Mгn = 1102000*0,95 = 1046900< Rb гb2 b´f h´f (ho- 0.5h´f)= =14.5(100)*0,9*50*6(31,5-0,5*6) = 11157750 Н см,
где ho = h-a = 41-5=36 см,
условие соблюдается , нейтральная ось проходит в полке;
Ao = Mгn/bf hoІ Rb гb2 = 1046900*1/50*31,5І*14.5(100)*0.9 = 0,015
По таблице 2.12 Мандриков находим з = 0,989, о = 0,016;
As = Mгn/з ho Rs = 1046900/0,989*31,5*280(100) = 1,2см²;
Принимаем из конструктивных соображений 2Ø9 A-II, As = 1,27 см²
Процент армирования:
µ = (As/bho)100 = 1,27*100/12*31,5 = 33 %
Расчет наклонного сечения лобового ребра на поперечную силу: Q =32,71 кН.
Вычисляем проекцию наклонного сечения на продольную ось с, придерживаясь порядка расчета:
цb2(1+цf + цn)Rbt гb2 bho² = 2*1.214*1.05*(100)* 12*31,5² = 3035570 Н/см,
где цn = 0
цf = 0.75(3h´f)h´f /bho = 0,75(3*6²)/12*31,5 = 0,214< 0,5;
(1+цf +цn) = (1+0.214+0) = 1.214 < 1.5.
В расчетном наклонном сечении Qb = Q/2, тогда
с = цb2(1+цf + цn)Rbt гb2 bho² /0.5Q = 3035570 / 0,5*32710 = 185,6см,
что больше 2ho= 2*31,5 = =63см; принимаем с =63см.
Вычисляем:
Qb = цb2(1+цf + цn)Rbt гb2 bho² /c = 3035570 /63 = 48183 Н =48,18 кН > Q = 32,71 кН,
Следовательно, поперечная арматура по расчету не требуется.
По конструктивным требованиям закрытые хомуты из арматуры диаметром 3 мм A-I шагом 150 см.
Консольный выступ для опирания марша армируют сеткой из арматуры диаметром 6 мм класса А-I
Расчет пристенного ребра. На пристенное ребро действуют следующие нагрузки: постоянная и временная, равномерно распределенные от половины пролета полки и от собственного веса:
q = (1650+5400)*1,5/2+347= 5634Н/м;
Определяем расчетный изгибающий момент в середине пролета ребра:
= ql²гn/8 = 5634*3,2²*0,95/8 = 6779 Н м.
Расчетное значение поперечной силы с учетом гn = 1:
Q = ql гn/2 =5634*3,2*0,95/2 = 8564 H.
Расчетное сечение пристенного ребра является тавровым с полкой в сжатой зоне шириной
b´f = 6h´f + br = 6*6 + 8 = 44 см.
Так как ребро монолитно связано с полкой, способствующей восприятию момента от консольного выступа, то расчет пристенного ребра можно выполнять на действие только изгибающего момента
М = 6779 Н м
В соответствии с общим порядком расчета изгибаемых элементов определяем (с учетом коэффициента надежности гn = 0.95 ) расположение нейтральной оси при х = h´fгn = 677900*095 = 644000 Н м < Rb гb2 b´f h´f (ho-0.5h´f)= =14.5(100)*0,9*44*6(15,5-0,5*6) = 4306500 Н см,
где ho = h-a = 20-4,5=15,5 см,
условие соблюдается , нейтральная ось проходит в полке;
Ao = Mгn/bf hoІ Rb гb2 = 644000/44*15,5І*14.5(100)*0.9 = 0,048
По таблице 2.12 Мандриков находим з = 0,975, о = 0,05;
As = Mгn/з ho Rs = 644000/0,975*15,5*280(100) = 1,522 см²;
Принимаем из конструктивных соображений 1Ø14 A-II, As = 1,539 см²
Процент армирования:
µ = (As/bho)100 = 1,539*100/12*15,5 = 0,82 %
Расчет наклонного сечения пристенного ребра на поперечную силу: Q =8,56кН.
Вычисляем проекцию наклонного сечения на продольную ось с, придерживаясь порядка расчета:
цb2(1+цf + цn)Rbt гb2 bho² = 2*1.44*1.05*(100)*12*15,5² = 571819 Н/см,
где цn = 0
цf = 0.75(3h´f)h´f /bho = 0,75(3*6²)/12*15,5 = 0,44 < 0,5;
(1+цf +цn) = (1+0.44+0) = 1.44 < 1.5.
В расчетном наклонном сечении Qb = Q/2, тогда с = цb2(1+цf + цn)Rbt гb2 bho² /0.5Q = 871819 / 0,5*8564 = 203,6см, что больше 2ho= 2*15,5 = 31см; принимаем с = 31см.
Вычисляем:
Qb = цb2(1+цf + цn)Rbt гb2 bho² /c = 871819 /31 = 18123 Н = 28,1 кН > Q = =8,56 кН,
Следовательно, поперечная арматура в пристенном ребре по расчету не требуется. По конструктивным требованиям принимаем диаметром 4 мм A-I шагом 150 см.
.4 Расчет сборной железобетонной колонны
Задание на проектирование. Рассчитать и сконструировать колонну среднего ряда первого этажа гаража в городе Омске с плоской крышей при случайных эксцентриситетах. Высота этажа Н=4 м. сетка колонн 6×6,3м. Глубина заложения фундамента 1,5м. здание возводится во ІІ климатическом районе по снеговому покрову. Временную и длительную нагрузку на междуэтажное перекрытие берем из расчета железобетонной плиты. Членение колонн двухэтажное. Стыки колонн располагаются на высоте 0,6 м. от уровня верха панелей перекрытия. Класс бетона В30, продольная арматура класса АІІІ. По назначению здание относится к одинадцатому классу. Принимаем гn=0,95
Решение. Определение нагрузок и усилий. Грузовая площадь от перекрытий и покрытий при сетке колонн6×6,3м. Агр=6*6,3=37,8 м2.
Подсчет нагрузок сведен в таблицу 2.4.1. При этом высота и ширина сечения ригеля приняты: h=1/15 l =1/15*6=0,4 м. и b=0,2 м
Таблица 2.4.1. нормативные и расчетные нагрузки.
|
Вид нагрузки |
Нормативная нагрузка, Н/м2 |
Коэффициент надежности по нагрузке гf |
Расчетная нагрузка, Н/м2 |
|
Постоянная: — мозаичный пол д=40мм.г=2200кг/м3 0,04∙22000= — пенобетон д=15мм.г=1200кг/м3 0,015∙12000= — железобетонная плита перекрытия |
880 180 2750 |
1,3 1,2 1,1 |
1140 216 3025 |
|
Итого: Временная: — кратковременная — длительная |
gn=3810 1500 — |
1.3 — |
g=4385 1950 — |
|
Всего от перекрытия От покрытия Постоянная:
|
qn=5310 150 400 133 40 2750 |
1,2 1,3 1,3 1,2 1,1 |
q=6335 180 520 172,9 48 3025 |
|
Итого: Временная: — кратковременная — длительна |
gn=3473 700 — |
1,4 — |
g=3945,9 980 — |
|
Всего от покрытия |
qn=4173 |
q=4925,9 |
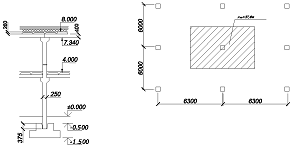
Сбор нагрузок на колонну.
Определяем вес конструкций действующих на колонну:
вес ригеля:
Gpn=b*h*l*с*2=0.2*0.4*6*25000*2=24000H
Gp= Gpn*1,1 =26400H
Вес покрытия и перекрытия:
Gпn=(qnпок+qnпер)Агр=(4173+5310)*37,8=358457Н
Gп=(qпок+qпер)Агр=(49259+6335)*37,5=425662Н
Вес колонны: определяем размеры сечения из условия гибкости, где длину l принимаем равную высоте этажа: л=l/h из этого следует, что при лmax=20(по табл. 2.15) h=400/20=20см принимаем кратное 5,но не менее 25см как для монолитных колонн, h=25см.
Gкn= b*h*l*с=0,25*0,25*7,18*25000=11219Н
Gк= b*h*l*с*гf =0,25*0,25*7,18*25000*1,1=12341Н
Определяем полную нормативную нагрузку
Nn=Gpn+Gпn+Gкn=24000+358457+11219=393676H
Полная расчетная нагрузка
гараж строительный перекрытие
N1= Gp+Gп+Gк=26400+425662+12641=464403H
Полная нагрузка от постоянной и длительной нагрузок:
Nld=[(4385+0)+(3946+0)]*37,8=314912H
Расчет колонны первого этажа.
Усилия с учетом гп=0,95
N1=464403*0,95=441183Н
Nld=314912*0,95=299166 Н
Предварительно вычисляем отношение Nld/ N1=299166/441183=0,7; гибкость колонны л=lо/hс=322/25=12,88 (где lо=[Н+0,6]∙ lо= =[4+0,6]*0,7=3,22 м.) принимаем 14, методом интерполяции по табл. 2.15 опр6еделяем коэффициенты цb=0.834, цr=0,866; эксцентриситет ео=hc/30=25/30=0,83см не меньше ео=l/600=460/600=0,767см принимаем большее значение ео=0,83см; расчетная длина колонны lо=322см<20*hc=20*25=500см,значит расчет продольной арматуры можно выполнить по формуле
(As +As’)=N1/ц*гs*Rs-A(Rb*гb2/Rsc)
Задаемся процентом армирования м=1% и вычисляем
б1=м*Rsc/Rbгb2=0.01*365/17*0,9=0,239
При Nld/ N1=0,7, л=lо/hс=14, по табл. 2.15 цb=0.834, цr=0,866,а коэффициент ц по формуле ц= цb+2*( цr -цb) б1=0,834+2*(0,866-0,834)0,239=0,849< цr=0.866;
Требуемая площадь сечения продольной арматуры
(As +As’)=N1/ц*гs*Rs-A(Rb*гb2/Rsc)=428643/0,849*1*365(100)-25*25*17*0,9/365=-12,34см2
несущая способность колонны не требует расчета арматуры, конструктивно принимаем 4Ø14 из условия гибкости стержня, УАs=6,16см2;м= 100*УАs/А=100*6,16/625=0,99%, что близко принятому м=1%.
Поперечную арматуру принимаем диаметром 4 мм класса А-1 шагом 200<20d1=20*14=280 мм.
Расчет консоли колонны. Расчетные данные для консоли колонны: бетон класса В30, арматура класса А-ІІІ, ширина консоли равна ширине колонны bc=25см. ширина ригеля b=20cм.
Решение. Максимальная расчетная реакция от ригеля перекрытия при гn=0,95, составляет Q= 26400*5,8*2,5*0,95=363660H=363кН,
lo= 6000-200=5800мм.
определяем минимальный вылет консоли
lpm=Q/b*Rb*гb2=363000/20*17(100)0.9=11,86 cм;
с учетом зазора между торцом ригеля и гранью колонны, равного 5см, вылет консоли
lс= lpm+5=11,86+5=16,86 см; принимаем кратно 5см lс=20см.
высоту сечения консоли находим по сечению проходящему по грани колонны. Рабочую высоту сечения определяем из условия
Q ≤ Rbt*bc*ho2/a,
где правую часть неравенства принимают не более 2,5 Rbt*bc*ho.
Выводим условия для ho:
ho< Q/ 2,5 Rbt*bc;
ho> √Qa/ 1,5 Rbt*bc .
определяем расстояние а от приложения опорной реакции Q до грани колонны
а=lc-Q/2b*Rb*гb2=20- 363000/2*20*17(100)0.9=14 cм.
Максимальная высота hо по условию
ho=Q/ 2,5 Rbt*bc=363000/2,5*1,2(100)0,9*25=54 см.
Минимальная высота
ho=√Qa/ 1,5 Rbt*bc= √363000*14/ 1,5*1,2(100)0,9*25=35,4 см.
Полная высота консоли у основания принята h=hо+3=54+3=57см.
Находим высоту свободного конца консоли, если нижняя грань ее наклонена под углом г=45˚,(tg45˚=1):
h1=h-lс tg45˚=57-20*1=37cм> h/3=57/3=19cм
условие удовлетворяется.
Расчет армирования консоли. Расчетный изгибающий момент по формуле
М=1,25Q(lc- Q/2b*Rb*гb)=1.25Qa= 1,25*363000*(20-363000/2*20*17*100*0,9=6383639Н*см=63,8 кН*см.
Коэффициент Ао по формуле
Ао=М/Rb*гb2*bc* ho2=6383639/17(100)0.9*25*542=0.05;
По табл. 2.12 находим з=0,974, о=0,052.
Требуемая площадь сечения продольной арматуры
As=M/з*ho*Rs=6383639/0.974*54*365(100)=1,763 cм2;
Принято 2Ø12 А-ІІІ, Аs=2,26 см2.Эту арматуру приваривают к закладным деталям консоли, на которые устанавливают и затем крепят на сварке ригель.
Армируем только наклонными хомутами по всей высоте консоли. Хомуты принимаем двухветвенными из стали класса А-І диаметром 5 мм, Аsw=0.196см2. шаг хомутов консоли назначаем из условий требования норм- не более 150мм и не более 1/4h=54/4=13,5см. принимаем шаг s=13см.
Литература
[Электронный ресурс]//URL: https://drprom.ru/kursovaya/stroitelstvo-garaja/
1. Байкалов В.И, Сигалов Э.Е. Железобетонные конструкции: Общий курс: Учебн. для вузов. — 4 издание; Стройиздан, 1985-728с
2. Мандриков А.П. Примеры расчета железобетонных конструкций: Учеб пос. для техн. — М.: Стройиздат, 1979.
3. Руководство по проектированию железобетонных конструкций покрытий и перекрытий. — М.: Стройиздат. — 1977 — 235с.
4. Цай Т.Н. Строительный конструкции: Учебн. для техн. — 2 издание — Стройиздат, 1985, — 462с.
5. ГОСТ 5781-82 «Сталь горячекатаная для армирования железобетонных
6. СНиП 2.03.01-84, Бетонные и железобетонные конструкции.
7. СНиП 2.01.01-82. Нагрузки и воздействия.
