Я выбралаэту тему потому что, на схемах Бернулли установление важные закономерностей теории вероятностей как математической науки, относящихся к сумме независимых случайных величин и представляющих закон больших чисел. Под законом больших чисел в теории вероятностей принято понимать ряд математических теорем, устанавливающих факт приближения средних характеристик большого числа испытаний к некоторым определенным постоянным. Важные теоремы, составляющие закон больших чисел, впервые были выведены для схемы испытаний Бернулли.
При практическом применении теории вероятностей часто приходится встречаться с задачами, в которых одно и то же испытание повторяется неоднократно. В результате каждого испытания может появиться или не появиться некоторое событие А, причем нас не интересует результат каждого отдельного испытания, а общее число появлений события А в результате серии опытов. Например, если производится группа выстрелов по одной и той же цели, нас, как правило, не интересует результат каждого выстрела, а общее число попаданий. В подобных задачах требуется уметь определять вероятность любого заданного числа появлений события в результате серии опытов. Такие задачи и будут рассмотрены. Они решаются весьма просто в случае, когда испытания являются независимыми.
Определение. Испытания называются независимыми, если вероятность того или иного исхода каждого из испытаний не зависит от того, какие исходы имели другие испытания.
Например, несколько бросаний монеты представляют собой независимые испытания.
Пусть произведено два испытания(n=2).
В результате возможно наступление одного из следующих событий:
Соответствующие вероятности данных событий такие:
или — наступление события только в одном испытании.
вероятность наступления события два раза.
вероятность наступления события только один раз.
вероятность наступления события нуль раз.
Пусть теперь n=3. Тогда возможно наступление одного из следующих вариантов событий:
Испытания автомобилей
... испытаниям. Автомобили текущего производства проходят контрольные, ресурсные, приемо-сдаточные и аттестационные испытания, а также испытания на надежность. Образцы всех автомобилей на ... результату воздействия; по определяемым характеристикам изделия; по стадиям жизненного цикла изделия. Испытания автомобилей ... сигнала в заданное число раз. По принципу действия преобразователи делятся на генераторные и ...
Соответствующие вероятности равны.
Очевидно, что полученные результаты при n=2 и n=3 являются элементами .
Теперь допустим, произведено n испытаний. Событие А может наступить n раз, 0 раз, n-1 раз и т.д. Напишем событие, состоящее в наступлении события А m раз
Необходимо найти число испытаний, в которых событие А наступит m раз. Для этого надо найти число комбинаций из n элементов, в которых А повторяется m раз, а n-m раз.
вероятность наступления события А.
(1)
Последняя формула называется формулой Бернулли и представляет собой общий член разложения :
Из формулы (1) видно, что ее удобно использовать, когда число испытаний не слишком велико.
Примеры
1. Бросается монета 7 раз. Найти вероятность наступления орла три раза.
Решение.
n=7, m=3.
Легко видеть, что пользоваться формулой Бернулли при больших значениях n достаточно трудно, так как формула требует выполнения действий над громадными числами. Естественно, возникает вопрос: нельзя ли вычислить интересующую нас вероятность, не прибегая к формуле Бернулли.
В 1730 г. другой метод решения при p=1/2 нашел Муавр; в 1783 г. Лаплас обобщил формулу Муавра для произвольного p, отличного от 0 и 1.
Эта формула применяется при неограниченном возрастании числа испытаний, когда вероятность наступления события не слишком близка к нулю или единице. Поэтому теорему, о которой идет речь, называют теоремой Муавра-Лапласа.
Теорема Муавра-Лапласа.
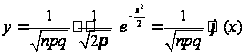
При
Имеются таблицы, в которых помещены значения функции
,
соответствующие положительным значениям аргумента x(см. приложение1).
Для отрицательных значений аргумента пользуются теми же таблицами, так как функция 
четна, т.е. 
.
Итак, вероятность того, что событие A появится в n независимых испытаниях ровно k раз, приближенно равна
,
где
№ 14. Вероятность поражения мишени стрелком при одном выстреле p=0,75.
Классификация испытаний и испытания РЭСИ на этапах проектирования, ...
... том, что путем многократных случайных испытаний (вычислений, производимых над случайными числами) определяют вероятность появления некоторого случайного события (математического ожидания случайной величины). ... воспроизводят случайные изменения указанных параметров. Частным видом статистических испытаний РЭСИ являются граничные испытания. Их проводят для определения зависимостей предельно допустимых ...
Найти вероятность того, что при 10 выстрелах стрелок поразит мишень 8 раз.
Решение. По условию n=10; k=8; p=0,75; q=0,25.
Воспользуемся формулой Лапласа:
.
Вычислим определяемое данными задачи значение x:
.
По таблице приложения1 находим
Искомая вероятность
.
Эта формула применяется при неограниченном возрастании числа испытаний, когда вероятность наступления события достаточно близка к 0 или 1.
,
где
Доказательство.
.
.
Таким образом получили формулу:
.
Примеры
№ 17. Вероятность изготовления негодной детали равна 0,0002. Найти вероятность того, что среди 10000 деталей только 2 детали будут негодными.
Решение. n=10000; k=2; p=0,0002. 
Искомая вероятность
.
№ 18. Вероятность изготовления бракованной детали равна 0,0004. Найти вероятность того, что среди 1000 деталей только 5 детали будут бракованными.
Решение. n=1000; k=5; p=0,0004.
Искомая вероятность
.
Теорема . Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна p, абсолютная величина отклонения относительной частоты появления события от вероятности появления события не превысит положительного числа , приближенно равна удвоенной функции Лапласа при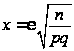 
:
Контроль размеров деталей с помощью предельных калибров
... деталей, но делает возможным появление бракованных деталей на сборке. Если изменение размеров происходят по закону нормального распределения, вероятность поступления на сборку бракованных деталей уменьшается. Четыре реальные схемы расположения допусков калибров ...
.
Доказательство. Будем считать, что производится n независимых испытаний, в каждом из которых вероятность появления события А постоянна и равна p. Поставим перед собой задачу найти вероятность того, что отклонение относительной частоты 
от постоянной вероятности p по абсолютной величине не превышает заданного числа 
. Другими словами, найдем вероятность осуществления неравенства
. (*)
Заменим неравенство (*) ему равносильными:
.
Умножая эти неравенства на положительный множитель
.
Тогда вероятность найдем следующим образом:
.
Значение функции
Примеры
№ 20. Вероятность того, что деталь не стандартна, p=0,1. Найти вероятность того, что среди случайно отобранных 400 деталей относительная частота появления нестандартных деталей отклонится от вероятности p=0,1 по абсолютной величине не более, чем на 0,03.
Решение. n=400; p=0,1; q=0,9;
,
имеем
.
По таблице приложения2 находим
№ 21. Вероятность того, что деталь не стандартна, p=0,1. Найти, сколько деталей надо отобрать, чтобы с вероятностью, равной 0,9544, можно было утверждать, что относительная частота появления нестандартных деталей(среди отобранных) отклонится от постоянной вероятности p по абсолютной величине не более чем на 0,03.
Решение. По условию, p=0,1; q=0,9; =0,03;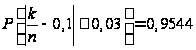 
. Требуется найти n. Воспользуемся формулой
Методы и средства для измерения внутренних и линейных размеров ...
... с заданной вероятностью пропуска дефектных заготовок, деталей и сборочных единиц при последующем изготовлении изделий. 1. МЕТОДЫ И СРЕДСТВА ИЗМЕРЕНИЙ 1.1 Выбор методов и средств измерений размеров в деталях типа “Корпус ... выбираем допускаемую погрешность. Допуск выбирается меньшим или равным данному. 1.1.1 Деталь типа «Корпус» Внутренние размеры: 1) Ø42H6 По ГОСТ 8.051-81 для диапазона размеров ...
.
в силу условия
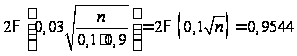
Следовательно,
По таблице приложения 2 находим
№ 22. Вероятность появления события в каждом из независимых испытаний равна 0,2. Найти, какое отклонение относительной частоты появления события от его вероятности можно ожидать с вероятностью 0,9128 при 5000 испытаниях.
Решение. Воспользуемся той же формулой, из которой следует:
.
1. Гмурман Е.В. «Теория вероятностей и математическая статистика», Москва, «Высшая школа»2013.
2. Гмурман Е.В. «Руководство к решению задач по теории вероятностей и математической статистике», Москва «Высшая школа»2014.
3. Гнеденко Б.В. «Курс теории вероятностей», Москва, «Наука»2015.
4. Колемаев В.А., Калинина В.Н., Соловьев В.И., Малыхин В.И., Курочкин А.П. «Теория вероятностей в примерах и задачах», Москва, 2012.
5. Вентцель Е.С. «Теория вероятностей», Москва, «Высшая школа»2015.
