Одномодовые оптические волокна

метки: Волокно, Одномодовое, Оптический, Дисперсия, Хроматический, Система, Прозрачность, Показатель

(а) (б)

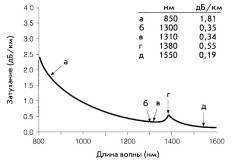
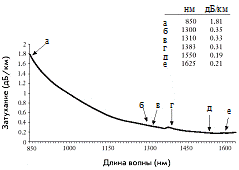
Рис. 9. Спектральные характеристики коэффициента затухания одномодовых оптических волокон CorningÒ: (а) волокно SMF-28ä; (б) LWPF волокно SMF-28eä.

На рис. 10 представлена спектральная характеристика коэффициента затухания многомодового оптического волокна CorningÒ 50/125.

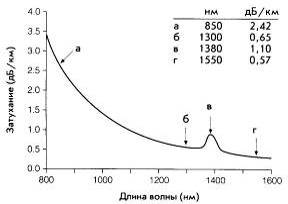
Рис. 10. Спектральная характеристика коэффициента затухания многомодового оптического волокна CorningÒ 50/125.

На длинах волн свыше 1600 нм начинают проявляться потери на инфракрасное поглощение, вызываемые колебаниями связи Si-O молекулы кварца SiO ₂ , а в ультрафиолетовой части спектра — из-за резонанса электронов, поэтому инфракрасное поглощение часто называют ионным, а ультрафиолетовое — электронным.

Величина потерь на инфракрасное поглощение a _ик пропорциональна показательной функции и уменьшается с ростом частоты по закону [16]:

где C и k — постоянные коэффициенты (для кварца k=0,7..0,9 мкм; С=0,9).

В 2002 рекордно минимальный коэффициент затухания a составил 0,154 дБ/км на длине волны l=1568 нм (Sumitomo Electric Industries Ltd.).

Предыдущий рекорд 0,154 дБ/км был установлен еще в 1986 г. и рассматривался как фактический предел. Сердцевина данного оптического волокна была изготовлена из чистого кварца, оболочка легирована фтором. Составляющие потерь принимали следующие значения: a _р =0,128 дБ/км; a_ик =0,014 дБ/км; примеси OH^— : 0,004 дБ/км; несовершенство ОВ: 0,004 дБ/км.

Потери в диапазоне l=1520…1606 нм не превышали 0,160 дБ/км.

Кабельные потери

Кабельные потери a _к обусловлены деформацией оптических волокон в процессе изготовления и прокладки кабеля. К ним относятся следующие факторы: скрутка; микро и макро изгибы; отклонение о прямолинейности; термомеханические воздействия на ОВ при наложении оболочек и покрытий; особенности технологии производства оптического кабеля.

При соблюдении технических условий (ТУ) на прокладку кабеля номинальный вклад со стороны кабельных потерь составляет не больше 20 % от полного затухания.

Оптические рефлектометры Оптические измерители мощности

... с первым. Измерение затухания оптических волокон и оптических кабелей методом обратного рассеяния По осциллограмме (рефлектограмме), полученной на экране оптического рефлектометра (рисунок 3), можно определить затухание всего волокна ... дисперсии. На конце ОВ устанавливается зеркало, отражающее световой импульс с коэффициентом отражения близким к 1. При измерении дисперсии осциллограф работает в ...

Потери на изгибах возникают по трем причинам:

Первая причина вызвана смещением модового пятна распространяющейся моды на некоторую величину относительно оптической оси сердцевины волокна, которая зависит от радиуса изгиба. Таким образом, в точке перехода прямого световода в изогнутый часть мощности основной моды передается модам высших порядков, которые для одномодовых оптических волокон фактически являются вытекающими и излучаемыми, и в конечном счете теряется (рис. 11).

Вторя причина обусловлена тем, что в изогнутом волокне периферийная часть моды распространяется ближе к границе сердцевина/оболочка быстрее, чем основная часть в центральной области сердцевины. В результате периферийная часть моды излучается в оболочку волокна и, в конечном счете, теряется. Величина этих потерь тем больше, чем больше число витков волокна и чем меньше радиус изгиба волокна.

Третья причина потерь на микроизгибах обусловлена тем, что часть мощности основной моды передается модам высших порядков, а в многомодовых оптических волокнах мощность сигнала также теряется, поскольку направляемые моды высших порядков преобразуются в вытекающие и излучаемые (рис. 11).

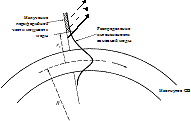
Рис. 11. Факторы потерь на макроизгибе оптического волокна.

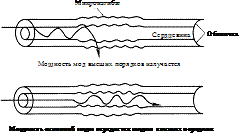
Рис. 12. Потери на микроизгиб.

6. Дисперсия оптических волокон

Дисперсией оптического волокна называют рассеяние во времени спектральных или модовых составляющих оптического сигнала. Основная причина дисперсии — разные скорости распространения отдельных составляющих оптического сигнала. Дисперсия проявляется как уширение, увеличение длительности распространяющихся по волокну оптических импульсов.

В общем случае указанная величина уширения оптического импульса Ds определяется непосредственно значениями среднеквадратической длительности на передающей s _in и s_out , соответственно:

с.

В свою очередь дисперсия создает переходные помехи, приводит к межсимвольной интерференции и, соответственно, ошибкам при приеме сигналов, что ограничивает скорость передачи в линии или, иными словами, длину регенерационного участка (РУ).

Межмодовая дисперсия

Межмодовая дисперсия характерна только для многомодовых оптических волокон. Она возникает в многомодовых световодах из-за наличия большого числа мод с различным временем распространения за счет различной длины пути, который отдельные моды проходят в сердцевине волокна (рис. 1.10 — 1.11).

Полоса пропускания типовых градиентных многомодовых оптических волокон характеризуется коэффициентом широкополосности DF, МГц∙км, значение которого указывается в паспортных данных на длинах волн, соответствующих первому и второму окнам прозрачности. Стандартные полосы пропускания типовых многомодовых оптических волокон составляют 400…2000 МГц∙км.

Реализация высокоскоростных многомодовых ВОЛП требует применения одномодовых лазеров в качестве источников излучения оптоэлектронных модулей ОСП, обеспечивающих скорость передачи данных свыше 622 Мбит/с (STM-4).

Оптические волокна

... важнейший параметр оптического волокна – дисперсия. Дисперсия – это рассеяние во времени спекртальных и модовых составляющих оптического сигнала. Существует три типа дисперсии: модовая дисперсия материальная дисперсия волноводная дисперсия Затухание и дисперсия у разных типов оптических волокон различны, Одномодовый ...

В свою очередь, основным фактором искажения оптических сигналов одномодовых ОСП, распространяющихся по волокнам многомодовых ВОЛП является уже не многомодовая дисперсия, а дифференциальная модовая задержка (DMD).

DMD носит случайный характер и зависит непосредственно от параметров конкретной пары «источник-волокно», а также от условий ввода излучения с выхода лазера в линейный тракт многомодовой ВОЛП. Поэтому в паспортных данных на новый тип многомодовых волоконных световодов — волокон, оптимизированных для работы с лазерами — помимо значений коэффициента широкополосности, позволяющего оценить величину межмодовой дисперсии при передаче сигналов многомодовых ОСП по многомодовым ВОЛП, также указываются дополнительные сведения, полученные в результате измерений DMD в процессе изготовления волокна, — например, предельная длина ЭКУ одномодовой ОСП Gigabit Ethernet.

Очевидно, что в одномодовых волоконных световодах межмодовая дисперсия не проявляется. Одними из основных факторов искажений сигналов, распространяющихся по одномодовым оптическим волокнам являются хроматическая и поляризационная модовая дисперсии.

Хроматическая дисперсия

Хроматическая дисперсия D _ch обусловлена конечной шириной спектра излучения лазера и различием скоростей распространения отдельных спектральных составляющих оптического сигнала. Хроматическая дисперсия складывается из материальной и волноводной дисперсии, и проявляется как в одномодовых, так и многомодовых оптических волокнах:

Материальная дисперсия

Материальная дисперсия D _mat определяется дисперсионными характеристиками материалов, из которых изготовлена сердцевина оптического волокна — кварца и легирующих добавок. Спектральная зависимость показателя преломления материала сердцевины и оболочки (рис. 13) вызывает изменения с длиной волны и скорости распространения.

Достаточно часто данная зависимость описывается известным уравнением Селлмейера, которое имеет следующий вид [48, 49]:

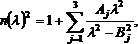
где A _j и B_j — коэффициенты Селлмейера, соответствующие заданному типу материала, легирующей примеси и ее концентрации.

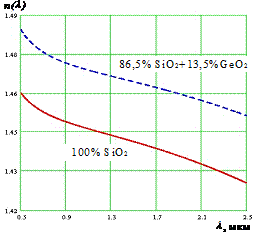
Рис. 13. Спектральная зависимость показателя преломления чистого кварца (сплошная кривая) и кварца, легированного 13,5% германием (штриховая кривая).

Очевидно, что эту характеристику для кварцевых волокон можно считать неизменной. Материальная дисперсия характеризуется коэффициентом D _mat пс/(нм^. км), который определяется из известного соотношения:

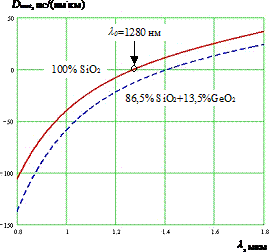
Рис. 14. Спектральная зависимость коэффициента материальной дисперсии чистого кварца (сплошная кривая) и кварца, легированного 13,5% германия (штриховая кривая).

В качестве примера, на рис. 14 представлены спектральные характеристики коэффициентов материальной дисперсии чистого кварца и кварца, легированного 13,5% германия.

Очевидно, что характер проявления материальной дисперсии зависит не только от ширины спектра излучения источника, но и от его центральной рабочей длины волны. Так, например, в области третьего окна прозрачности l=1550 нм менее длинные волны распространяются быстрее, чем более длинные, а материальная дисперсия больше нуля (D _mat >0).

Данный диапазон получил название области нормальной или положительной дисперсии (рис. 1.26 (б)).

В области первого окна прозрачности l=850 нм, напротив, более длинные волны распространяются быстрее, чем короткие, а материальной дисперсии соответствует отрицательное значение (D _mat <0).

Данный диапазон называется областью аномальной или отрицательной дисперсии (рис. 15 (в)).

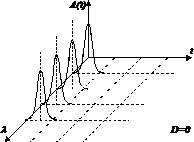
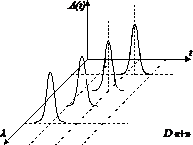
(а) (б)

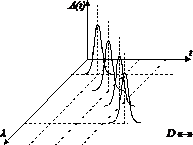
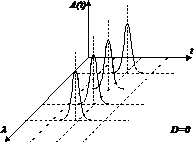
(в) (г)

Рис. 15. Хроматическая дисперсия: (а) импульс на входе ВОЛП; (б) нормальная дисперсия; (в) аномальная дисперсия; (г) область нулевой дисперсии.

В некоторой точке спектра, называемой точкой нулевой материальной дисперсии l ₀ , происходит совпадение, при этом и короткие, и длинные волны распространяются с одинаковой скоростью (рис. 16 (г)).

Так, например, для чистого кварца SiO₂ точка нулевой материальной дисперсии соответствует длине волны 1280 нм (рис. 15).

Волноводная дисперсия

Волноводная дисперсия D _w обусловлена зависимостью групповой скорости распространения моды от длины волны, характер которой определяется формой профиля показателя преломления оптического волокна. Указанная зависимость определяется пространством, занимаемым модой по отношению к профилю показателя преломления волокна. Так, в ряде случаев в световодах с большим диаметром сердцевины волноводной дисперсией можно пренебречь. В одномодовых оптических волокнах из-за малого радиуса сердцевины, напротив, волноводная дисперсия достаточно велика. Достаточно часто для оценки волноводной дисперсии используют следующее соотношение [48]:

где V — нормированная частота, значение которой определяется по формуле (1.11);

b — нормированная постоянная распространения, которая связана с b следующим соотношением:

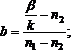
при этом составляющая формулы (1.29) получила название нормированный параметр волноводной дисперсии.

Спектральные характеристики хроматической дисперсии одномодовых оптических волокон действующих рекомендаций МСЭ-Т

Результирующее значение хроматической дисперсии D _ch , которое складывается из материальной D_mat и волноводной D_w составляющих (рис. 16), непосредственно связано с первой и второй производной постоянной распространения следующим соотношением [48]:

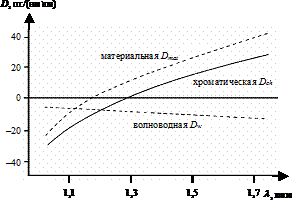
Рис. 16. Хроматическая дисперсия одномодовых оптических волокон рек. МСЭ-Т G.652.

Очевидно, что подбор профиля показателя преломления позволяет соответствующим образом изменить итоговую спектральную характеристику хроматической дисперсии.

Так, в волокнах SSF, которые характеризуются типовым ступенчатым профилем показателя преломления, преобладает положительная материальная дисперсия, которая и формирует минимум хроматической дисперсии в области длины волны 1300 нм (рис. 17) [48, 50].

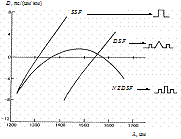
Рис. 17. Хроматическая дисперсия одномодовых оптических волокон SSF (рек. МСЭ-Т G.652)

Профили показателя преломления волокон DSF и NZDSF сформированы таким образом, чтобы компенсировать материальную дисперсию отрицательной волноводной. В волокнах DSF при сложении материальной и волноводной составляющих дисперсии длина волны нулевой дисперсии смещается в область третьего окна прозрачности l=1550 нм. Для волокон NZDSF длина волны нулевой дисперсии не нормируется. Она обычно находится за пределами диапазона длин волн третьего окна прозрачности (диапазона C).

Дисперсионные параметры одномодовых оптических волокон

Хроматическая дисперсия характеризуется коэффициентом хроматической дисперсии D, имеющим размерность пс/(нм ^. км), значение которого в паспортных данных достаточно часто указывается на длинах волн, соответствующих второму и третьему окнам прозрачности (1310 и 1550 нм).

В качестве примера, в табл. 7 приведены типовые значения коэффициента хроматической дисперсии D волокон рек. МСЭ-Т G.652 и G.653.

Таблица 7.

D, пс/(нм.км)	DSF (G.653)
l=1310 нм	£ 2,7…3,5	£ 25
l=1550 нм	£ 17…18	£ 2,7

Кроме параметра D в качестве характеристик хроматической дисперсии оптических волокон также используют коэффициент наклона дисперсионной характеристики S ₀ , который имееет размерность пс/(нм^2. км) и относительный коэффициент наклона дисперсионной характеристики RDS=S₀ /D с размерностью 1/нм. Последняя величина однозначно связана с полосой пропускания оптического волокна и характеризует поведение дисперсионной характеристики в заданном диапазоне длин волн.

Выше было отмечено, что на сегодняшний день, благодаря усовершенствованию технологии производства оптических волокон стала доступна вся область низких потерь от 1260 нм до 1675 нм. В общем случае значение коэффициента хроматической дисперсии D волокон SSF на конкретной несущей l из заданного спектрального диапазона оценивается по следующей формуле [48, 54]:

Значения коэффициент наклона дисперсионной характеристики S ₀ и длины волны нулевой дисперсии также указываются в паспортных данных на оптические волокна. Например, указанные параметры одномодового оптического волокна CorningÒ SMF-28eÔ составляют: S₀ =0,092 пс/(нм^2. км); l₀ =1301,5…1321,5 нм [48].

Для волокон со смещенной дисперсией (DSF) величина D на определенной несущей l из заданного спектрального диапазона оценивается по следующей интерполяционной формуле [48, 50]:

,

В ряде случаев (в частности, для одномодовых оптических волокон NZDSF) указываются значения коэффициентов хроматической дисперсии на длинах волн l ₁ и l₂ , соответствующих границам спектральных диапазонов (l₁ …l₂ ) — например, диапазонам С и L, и формула вычисления D(l) (l₁ <l<l₂ ) определяется непосредственно значениями D(l₁ ) и D(l₂ ):

В качестве примера в табл. 8 приведены значения коэффициента хроматической дисперсии D для волокон CorningÒ LEAFÒ на границах диапазонов C и L [48].

Таблица 8.

D, пс/(нм.км)
Диапазон C		Диапазон L
1530 нм	1565 нм	1565 нм	1625 нм
2,0	6,0	4,5	11,2

Максимально допустимое значение хроматической дисперсии на РУ ВОЛП при передаче сигналов со скоростью B, Гбит/с, при условии приращения уровня помех не более чем на 1 дБ, приближенно определяется из следующего соотношения:

пс/нм

Результаты оценки дисперсии ВОЛП и максимальная протяженность РУ, в пределах которого не требуется проведение дополнительных мероприятий по компенсации дисперсии, для волокон SSF и NZDSF на длине волны l=1550 нм представлены в табл. 9 [48].

Таблица 9.

B, Гбит/с	2,5	10	40
SDH: STM-	16	64	256
Дисперсия, DРУ max пс/нм	16640	1040	65
Lmax, км: ОВ SSF (l=1550 нм, D=17 пс/(нм.км))	980	62	4
Lmax, км: ОВ NZDSF (l=1550 нм, D=4,4 пс/(нм.км))	3782	236	14

Заключение

Допустимая величина дисперсии на выходе ВОЛП при скорости передачи 2,5 Гбит/с составляет 16640 пс/км. Данной величине соответствуют предельные значения длины РУ 980 км для волокон SSF и 3782 км для волокон NZDSF. Таким образом, сигналы ОСП уровня STM-16 на рабочей длине волны, соответствующей третьему окну прозрачности, можно передавать по волокнам особенно со смещенной дисперсией практически на неограниченное расстояние. Но уже при скорости передачи 10 Гбит/с (STM-64) допустимая величина дисперсии уменьшается до 1040 пс/нм, и если для волокон NZDSF значение L _max уменьшается до 236 км, то максимальная длина РУ ВОЛП на основе волокон SSF не превышает 62 км. В этом случае увеличение протяженности РУ потребует проведения дополнительных мероприятий по компенсации дисперсии.

одномодовый оптический волокно дисперсия

Список использованной литературы

[Электронный ресурс]//URL: https://drprom.ru/kursovaya/odnomodovoe-volokno/

Федеральный закон: Выпуск 86. О связи. — М.: Инфра. -М, 2012.

Волоконно-оптические системы передачи: Учебник для вузов / М.М. Бутусов, С.М. Верник, С.Л. Галкин и др. — М.: Радио и связь, 2002. — 416 с.

Носов Ю.Р. Оптоэлектроника. — 2е изд., перераб и доп. — М.: Радио и связь, 2009. — 360 с.

Убайдуллаев Р.Р. Волоконно-оптические сети. — М.: ЭКО-ТРЕНДЗ, 2008. — 267 с.

Бакланов И.Г. Технологии измерений первичной сети. Часть I. Системы Е1, PDH, SDH. Часть 2. Системы синхронизации, B-ISDN, АТМ. — М.: ЭКО-ТРЕНДЗ, 2010.

Иванов А.Б. Волоконная оптика. Компоненты, системы передачи, измерения. — М.: SYRUS SYSTEMS, 2009. — 671 с.

Листвин А.В., Листвин В.Н., Швырков Д.В. Оптические волокна для линий связи. — М.: ЛЕСАРарт, 2003. -288с.

Гауэр Дж. Оптические системы передачи. Пер с англ. — М.: Радио и связь, 2009. — 501 с.

Слепов Н.Н. Современные технологии цифровых оптоволоконных сетей связи (АТМ, PDH, SDH, SONET и WDM).

— М.: Радио и связь, 2000. — 468 с.

Волоконно- оптические системы передачи и кабели. Справочник / Гроднев И.И., Мурадян Р.М. и др. — М.: Радио и связь, 2003. — 264 с.

Шевцов Э.А., Белкин М.Е. Фотоприемные устройства волоконно-оптических систем передачи. — М.: Радио и связь, 2002. — 230 с.

Волоконно-оптическая техника: история, достижения, перспективы. Сб. статей под ред. Слепова Н.Н., Дмитриева С.А. — М.: Connect. 2000, — 376 с.

Заславский К.Е. Волоконно-оптические системы передачи (ВОСП).

Учебное пособие. Часть 1. — Новосибирск, НЭИС, 2004. — 76 с.

Заславский К.Е. ВОСП. Учебное пособие. Часть 2. — Новосибирск СибГАТИ, 2005, — 68 с.

Заславский К.Е. Волоконная оптика в системах связи и коммутации. Учебное пособие. Часть 2. — Новосибирск, СибГУТИ, 2009. — 122 с.

Фокин В.Г. Волоконно-оптические системы передачи с подвесными кабелями на воздушных линиях электропередачи и контактной сети железных дорог. — Новосибирск, СибГУТИ, 2000. — 94 с.

Фокин В.Г. Аппаратура и сети доступа. — Новосибирск, СибГУТИ, 2000. — 114 с.