Электрические цепи второго порядка повсеместно применяются в электротехнике. В данных цепях имеют место процессы без которых невозможно подключение различного рода коммутационной аппаратуры. Это в свою очередь подразумевает наличие большого объема всякого рода вычислений, которые обычному человеку-энергетику крайне сложно вычислить. Именно поэтому существуют и разрабатываются системы компьютерной математики. Системы компьютерной математики типа М athcad и Scilab наиболее приспособленные для расчетов в энергетике. Ведь там используются преобразования и работа с математическими выражениями в аналитической (символьной) форме.
Применение компьютерной математики существенно расширяет возможности автоматизации всех этапов математического моделирования, а также позволяют провести исследование проблемы, анализ данных, моделирование, тестирование, проверку существования решения, оптимизацию, документирование и оформление результатов, они позволяют сосредоточить основное внимание на существе проблемы, оставляя в стороне технику классической математики, детали вычислительных методов и алгоритмических процедур, нюансы языков программирования и команд операционной системы.
В данной курсовой работе требуется проанализировать как влияет изменение параметров на электрическую цепь второго порядка используя системы компьютерной математики(СКМ) — MathCad и Scilab , которые являются отличным примером системы компьютерного моделирования.
1 . Математические модели технических объектов и численные методы для их реализации
1.1 Математические модели и моделирование технического объекта
электрический компьютерный математика моделирование
На пути реализации в технике наиболее перспективных научных открытий и разработок обычно стоят препятствия, связанные с отсутствием или ограниченными возможностями конструкционных или функциональных материалов и с недостаточностью достигнутого технологического уровня. Поэтому процесс реализации научных и технических идей — это процесс поиска разумного компромисса между желаемым и возможным. Этим компромиссом является математическая модель.
Использование методов подобия и анализа размерностей в компьютерном ...
... практикой прикладной математики и компьютерного моделирования: эвристические рассуждения, навыки в выполнении преобразований, а также содержательная интуиция являются здесь существенными элементами. Анализ размерностей позволяет нам ... себя определение относящихся к делу величин и формулировку системы определяющих уравнений, которые описывают проблему в подробностях. На втором шаге мы можем ...
Математической моделью (ММ) называют совокупность математических объектов (чисел, переменных, матриц, множеств и т. п.) и связей между ними, отображающих важнейшие для проектирования свойства технического объекта (ТО).
Выполнение проектных операций и процедур в САПР основано на оперировании ММ. С их помощью прогнозируются характеристики и оцениваются возможности предложенных вариантов схем и конструкций, проверяется их соответствие предъявляемым требованиям, проводится оптимизация параметров, разрабатывается техническая документация и т. д.
Моделирование — это изучение объекта путем построения и исследования его модели, осуществляемое с определенной целью, состоящее в замене эксперимента с оригиналом экспериментом на модели.
Для обсуждения и обоснования основных подходов к разработке проблем математического моделирования технических устройств и процессов в них представляется целесообразным предварительно рассмотреть условную схему, определяющую последовательность проведения отдельных этапов общей процедуры вычислительного эксперимента. Исходной позицией этой схемы служит технический объект (ТО), под которым будем понимать конкретное техническое устройство, его агрегат или узел, систему устройств, процесс, явление или отдельную ситуацию в какой-либо системе.
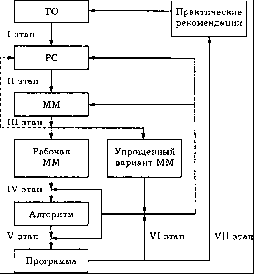
Рисунок 1- Условная схема математичекского моделирования
На первом этапе осуществляют неформальный переход от рассматриваемого (разрабатываемого или существующего) ТО к его расчетной схеме( PC ).
При этом в зависимости от направленности вычислительного эксперимента и его конечной цели акцентируют те свойства, условия работы и особенности ТО, которые вместе с характеризующими их параметрами должны найти отражение в PC , и, наоборот, аргументируют допущения и упрощения, позволяющие не На первом этапе осуществляют неформальный переход от рассматриваемого (разрабатываемого или существующего) ТО к его расчетной схеме( PC ).
При этом в зависимости от направленности вычислительного эксперимента и его конечной цели акцентируют те свойства, условия работы и особенности ТО, которые вместе с характеризующими их параметрами должны найти отражение в PC , и, наоборот, аргументируют допущения и упрощения, позволяющие не учитывать в PC те качества ТО, влияние которых предполагают в рассматриваемом случае несущественным. Иногда вместо PC используют термин содержательная модель ТО, а в некоторых случаях — концептуальная модель. В сложившихся инженерных дисциплинах (например, в сопротивлении материалов, электротехнике и электронике) помимо описательной (вербальной) информации для характеристики PC разработаны специальные приемы и символы наглядного графического изображения. По ряду новых направлений развития техники подобная символика находится в стадии формирования. При разработке новых ТО успешное проведение первого этапа в значительной мере зависит от профессионального уровня инженера, его творческого потенциала и интуиции. Полнота и правильность учета в PC свойств ТО, существенных с точки зрения поставленной цели исследования, являются основной предпосылкой получения вдальнейшем достоверных результатов математического моделирования. И наоборот, сильная идеализация ТО ради получения простой PC может обесценить все последующие этапы исследования.
Этапы жизненного цикла услуги безопасности
... все полученные в ходе исследования результаты, сформулированы выводы по каждой задаче исследования и его цели. Такой отчет становится важным основанием для принятия решения о начале производства и реализации услуги безопасности. информирование потенциальных ...
Содержание второго этапа состоит, по существу, в формальном, математическом описании PC . Это описание в виде математических соотношений, устанавливающих связь между параметрами, характеризующими PC ТО, и называют математической моделью (ММ).
Надо сказать, что для некоторых типовых
На третьем этапе проводят качественный и оценочный количественный анализ построенной ММ. При этом могут быть выявлены противоречия, ликвидация которых потребует уточнения или пересмотра PC (штриховая линия на рисунок 1).
Количественные оценки могут дать основания упростить модель, исключив из рассмотрения некоторые параметры, соотношения или их отдельные составляющие, несмотря на то что влияние описываемых ими факторов учтено в PC . В большинстве случаев, принимая дополнительные по отношению к PC допущения, полезно построить такой упрощенный вариант ММ, который позволял бы получить или привлечь известное точное решение. Это решение затем можно использовать для сравнения при тестировании результатов на последующих этапах. В некоторых случаях удается построить несколько ММ для одного и того же ТО, отличающихся различным уровнем упрощения.
Построение иерархии ММ связано с различной детализацией свойств изучаемого ТО. Сравнение результатов исследования различных ММ может существенно расширить и обогатить знания об этом ТО. Кроме того, такое сравнение позволяет оценить достоверность результатов последующего вычислительного эксперимента: если более простая ММ правильно отражает некоторые свойства ТО, то результаты исследования этих свойств должны быть близки к результатам, полученным при использовании более полной и сложной ММ.
Производственная программа и её содержание
... быть применены штрафные санкции. 3. Показатели и этапы разработки производственной программы При разработке производственной программы предприятия применяются натуральные, трудовые и ... будут использованы для выработки управленческих решений и производственно программы. 2. Понятие и назначение производственной программы Производственная программа определяет необходимый объем производства продукции ...
Итог анализа на рассматриваемом этапе — это обоснованный выбор рабочей ММ ТО,
Четвертый этап состоит в обоснованном выборе метода количественного анализа ММ, в разработке эффективного алгоритма вычислительного эксперимента, а пятый этап — в создании работоспособной программы, реализующей этот алгоритм средствами вычислительной техники. Для успешного проведения четвертого этапа необходимо владеть арсеналом современных методов вычислительной математики, а при математическом моделировании довольно сложных ТО выполнение пятого этапа требует профессиональной подготовки в области программирования на ЭВМ.
Получаемые на шестом этапе (в итоге работы программы) результаты вычислений должны прежде всего пройти тестирование путем сопоставления с данными количественного анализа упрощенного варианта ММ рассматриваемого ТО. Тестирование может выявить недочеты как в программе, так и в алгоритме и потребовать доработки программы или же модификации и алгоритма и программы. Анализ результатов вычислений и их инженерная интерпретация могут вызвать необходимость в корректировке PC и соответствующей ММ.
После устранения всех выявленных недочетов триаду „модель — алгоритм — программа “ можно использовать в качестве рабочего инструмента для проведения вычислительного эксперимента и выработки на основе получаемой количественной информации практических рекомендаций, направленных на совершенствование ТО, что составляет содержание седьмого, завершающего „технологический цикл ” этапа математического моделирования.
Представленная последовательность этапов носит общий и универсальный характер, хотя в некоторых конкретных случаях она может и несколько видоизменяться. Если при разработке ТО можно использовать типовые PC и ММ, то отпадает необходимость в выполнении ряда этапов, а при наличии и соответствующего программного комплекса процесс вычислительного эксперимента становится в значительной степени автоматизированным. Однако математическое моделирование ТО, не имеющих близких прототипов, как правило, связано с проведением всех этапов описанного „технологического цикла » .[3]
Целью моделирования являются: получение, обработка, представление и использование информации об объектах, которые взаимодействуют между собой и внешней средой; а модель здесь выступает как средство познания свойств и закономерности поведения объекта.
Задача о мостах леонард эйлер и теория графов
... таких задач также входит в теорию графов. Впервые его исследовал в 1736 году великий немецкий математик Леонард Эйлер, решая задачу о Кенигсбергских мостах. Поэтому графы, которые можно нарисовать указанным способом, называются Эйлеровыми графами. Задача 1 ...
1.2 Применение численных методов в моделировании
Дифференциальные уравнения, которые можно проинтегрировать известными методами, встречаются сравнительно редко. В связи с этим особое значение приобретают приближенные методы решения дифференциальных уравнений. Эти методы делятся на две группы:
а) аналитические;
б) численные.
Применение аналитических методов дает приближенное решение в виде аналитического выражения, численных — в виде таблицы численных значений.
Наиболее распространенными из численных методов, применяемых в математическом моделировании, являются метод Эйлера и метод Рунге-Кутта четвертого порядка.
Метод Эйлера основан на непосредственной замене производной разностным отношением по приближенной формуле. По методу Эйлера в формуле Тейлора не учитываются члены, содержащие производные второго и более высокого порядка. Метод Эйлера имеет первый порядок точности, откуда следует, что для достижения высокой точности требуется мелкий шаг, что экономически не выгодно. Достоинством метода является его простота. Метод Эйлера используют для более точных многошаговых методов.
Пусть требуется решить задачу Коши: найти решение дифференциального
у=у
При численном решении уравнения задача ставится так:
в точках х
Х
Приближенно можно считать, что правая часть уравнения остается постоянной на каждом из отрезков между точками деления. Метод Эйлера состоит в непосредственной замене производной разностным отношением по приближенной формуле:
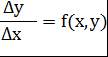
В силу сделанных предположений на первом отрезке искомое решение приближенно представляется линейной функцией:
(1.5)
![]()
В частности, при
y
Равенство означает, что на отрезке [х
y
Для точки
![]()
Таким образом, в качестве приближения искомой интегральной кривой получаем линию, изображенную на рисунке 1.1, с вершинами в точках М 0 (х 0 , уо), M 1 (y1, y 2),…. М п (х п , у п ).
Рентгеновский метод неразрушающего контроля
... методов неразрушающего контроля – дефектоскопии, основанных на исследовании изменений физических характеристик металла. При использовании неразрушающих методов контроля ... материала. Рис.1. Схема рентгеновского просвечивания: 1 — источник рентгеновского излучения; 2 — пучок рентгеновских лучей; 3 ... технологические карты контроля, которые определяют порядок и технику контроля с использованием ...

Рисунок 1.1 — График искомой интегральной кривой
Вычисление приближений у
Этот метод дает весьма грубое приближение решения задачи Коши. Он обычно используется в случае, когда необходимо получить примерное представление о решении на небольшом промежутке.Если функция f ( x ,у) в уравнении на некотором отрезке в рассматриваемой области непрерывна по х и удовлетворяет условию Липшица по у:
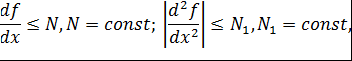
![]()
Погрешность обыкновенного метода Эйлера оценивается формулой:
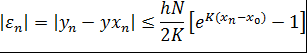
Метод Рунге-Кутта является одним из наиболее употребительных численных методов повышенной точности. Низкая точность метода Эйлера связана в первую очередь с тем, что остаточный член формулы Эйлера велик.
Очевидно, что для уменьшения погрешности вычисления необходимо увеличить количество учитываемых членов в формуле Тейлора. Наиболее распространенным является метод Рунге-Кутта 4-го порядка, в котором учтены производные до 4-го порядка включительно. Метод Эйлера можно рассматривать как метод Рунге-Кутта 1-го порядка. Метод Рунге-Кутта требует большого объёма вычислений, однако расчёт оказывается более точным, чем расчёт по методу Эйлера с тем же шагом.
Величина погрешности метода оценивается с помощью правила Рунге. Значение оценки Рунге состоит в том, что погрешность оценивается через величины, получаемые непосредственно в процессе счёта. На этой формуле основан метод автоматического выбора шага в процессе счёта в стандартных программах.
Импульсный стабилизатор напряжения
... импульсные преобразователи напряжения преобразуют постоянный ток на входе в постоянный ток на выходе. Для питания устройств от сети переменного тока необходимо устанавливать на входе выпрямитель и сглаживающий фильтр. Стоит отметить, что импульсный стабилизатор напряжения ... на выходе имеем усреднённое значение напряжения, которое зависит от входного напряжения и скважности импульсов с небольшой ...
Эти методы являются одноступенчатыми: чтобы найти у
Они согласуются с рядом Тейлора вплоть до членов порядка hp
Они не требуют вычисления производных от f(x
Наиболее точный метод решения — метод Рунге-Кутта 4 порядка, один из самых употребляемых методов интегрирования дифференциальных уравнений
Его особенности:
а) этот метод является одноступенчатым и одношаговым;
б) требует информацию только об одной точке;
в) имеет небольшую погрешность;
г) значение функции рассчитывается при каждом шаге;
Формулы, описывающие классический метод Рунге-Кутта четвертого порядка, состоят из следующих пяти соотношений:
y
R
Ошибка ограничения для этого метода равна:
e
[6]
.3 Использование численных методов в системе
Рассмотрим один из самых распространенных численных методов в СКМMathCAD
Для решения дифференциальных уравнений и систем уравнений из-за его высокой точности часто применяется метод Рунге-Кутта. Отличительная особенность метода — уточнение наклона интегральной кривой за счет вычисления производной не только в начале текущего отрезка интегрирования, но и, например, в середине отрезка (для двучленных схем Рунге-Кутта) или четырехкратное вычисление производных в методе четвертого порядка.
Рассмотрим задачу Коши :
![]()
![]()
Тогда приближенное значение в последующих точках вычисляется по итерационной формуле 1.3:
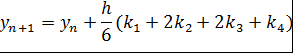
Вычисление нового значения проходит в четыре стадии:
![]()
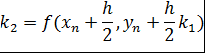
Преобразователи напряжение-ток
... линейности можно представить как: преобразователь ток напряжение , (8а) где SМАКС максимальное значение крутизны на участке U0. ... дифференциального каскада Оценку нелинейности преобразования напряжения в ток для схемы рисунка 5 можно произвести следующим образом. ... оценки погрешности такого преобразователя, обусловленной нелинейностью, может служить нахождение отклонения реальной функции IХ /I0 ...
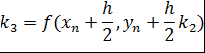
![]()
где
Метод Рунге-Кутта легко переносится и на случай системы дифференциальных уравнений.
В
)
где у — вектор начальных условий размерности
Начальные условия, заданные в векторе у, — это значения решения в точке х
2 . Алгоритмический анализ задачи
2.1 Полная постановка задачи, С использованием системы
.1 Рассчитать значения функций напряжения на конденсаторе и тока в цепи без учета гармонического воздействия U ( t ).
Построить графики этих функций.
.2 Рассчитать значения функций напряжения на конденсаторе и тока в цепи с учетом гармонического воздействия U ( t ).
Построить графики этих функций.
.3 Для функции напряжения, полученной в п.1.1, исследовать влияние индуктивности
С использованием системы
1.4 Считать файлы данных, полученные в п.1.3. Построить сводный график функций напряжения. Построить график зависимости минимумов напряжений от индуктивности.
.5 Выполнить аппроксимацию полученной зависимости, построить график исходной и аппроксимирующей функций.
.6 Для функции тока
2.2 Анализ исходных и результирующих данных
Исходными данными для работы являются:
С — значение емкости конденсатора;
С =1.05∙10 -3 Ф
Датчики тока и напряжения
... напряжения. Также напряжение можно измерить датчиками напряжения, основанные на эффекте Холла. Схематическое изображение измерения напряжения датчиком Холла замкнутого типа представлено на рисунке 7. , Рисунок 7 - Измерение напряжения датчиком Холла замкнутого типа Это тот же датчик тока ...
R — исходное сопротивление;
R =56 Ом
L 1 , L 2 — значения индуктивностей;
L 1 =0.025 Гн
L 2= 0.05 Гн
U ( t ) — исходная функция гармонического воздействия;
Um — амплитуда гармонического воздействия;
Um = 4 В
ω — частота;
ω = 460 Гц
Т — время исследования.
Т= 0,55 с
Таблица 2.1 — Значения варьируемого параметра
-
Начальные значения для расчета п.1.1: U C (0)=0.1, i 2 (0)=1В, i 1 (0)=0
Результатами расчетов являются:
значения функций напряжения на конденсаторебез учета гармонического воздействия U ( t ).
значения функций напряжения на конденсаторес учетом гармонического воздействия U ( t ).
зависимость минимального значения напряжения на конденсаторе от значения индуктивности L 1.
график зависимости минимумов напряжений от индуктивности
аппроксимация зависимости минимумов напряжений от индуктивности
время, при котором ток i 2 достигает порогового значения, равного -0.005.
2.3 Описание математической модели
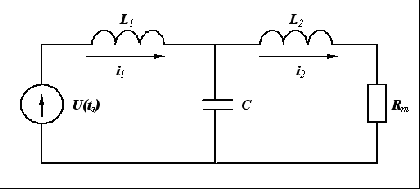
Рисунок 2.1 — Линейная электрическая цепь системы
Работу цепи, приведенной на рисунке, описывает система дифференциальных уравнений вида:
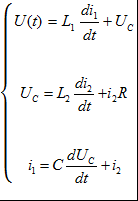 (2.1)
(2.1) Для их решения преобразуем систему в следующий вид:
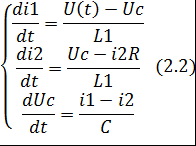
После замены переменных система примет вид:
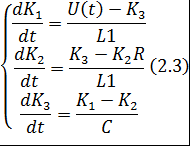
Для случая, где значение ЭДС не учитывается:
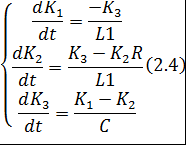
При решении системы ОДУ находим функции i 1( t ) , i 2( t ), Uc ( t )
2.4 Графическая схема алгоритма
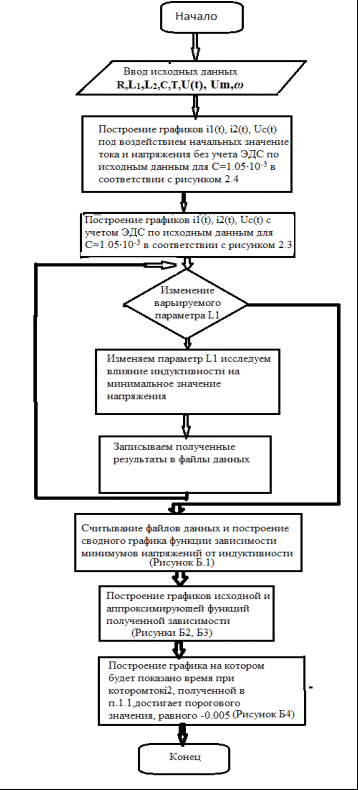
Рисунок 2.2 — Схема алгоритма решения задачи
3. Описание реализации задачи
.1 Описание реализации базовой модели
Задача состоит в том, чтобы решить данные дифференциальные уравнения без учёта ЭДС. Для решения поставленной задачи введем исходные данные. С использованием системы MathCAD рассчитываем значения функций тока и напряжения в заданной электрической схеме. Для этого с помощью функции rkfixed (метод Рунге — Кутта) решаем систему дифференциальных уравнений (2.2), которая является математической моделью поставленной задачи. В системе ДУ(рисунок 2.4) k 1 — значение тока i 1, k 2 — значение тока i 2, k 3 — значение напряжения Uc . Выводим таблицу значений времени (Приложение А), напряжений на обоих конденсаторах и тока. В которой первый столбец — значение времени Т, второй столбец — значение силы тока I 1, третий столбец — значение силы тока I 2, четвертый столбец-значение напряжения U с.
Строим графики зависимости тока i 1( t )( Рисунок А.2), напряжения на конденсаторе Uc ( t )( Рисунок А.3) и силы тока i 2( t )( Рисунок А.4).

Рисунок А.2 Зависимость тока i 1 от времени.
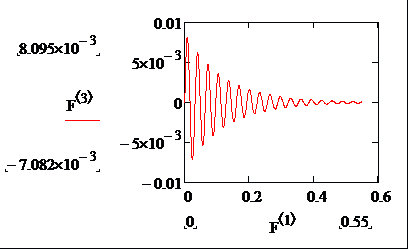
Рисунок А.3 Зависимость тока i 2 от времени.
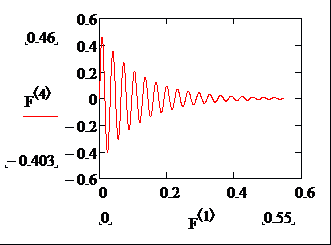
Рисунок А.4 Зависимость напряжения Uc на конденсаторе от времени.
Аналогично решаем систему дифференциальных уравнений(2.2) с учетом ЭДС. В самом решении меняем лишь вектор исходных данныхк и вектор, содержащий первые производные функций. В вектор к вписываем нулевые значения. В результате получаю значения функции тока на катушке индуктивности и напряжений на конденсаторах в заданной электрической схеме с ЭДС.
Выводим таблицу значений времени, напряжений на обоих конденсаторах и тока.В которой первый столбец — значение времени Т, второй столбец — значение силы тока I 1, третий столбец — значение силы тока I 2, четвертый столбец-значение напряжения U с.(Рисунок А.6)
Строим графики зависимости i 1( t ), Uc ( t ) и i 2( t ).
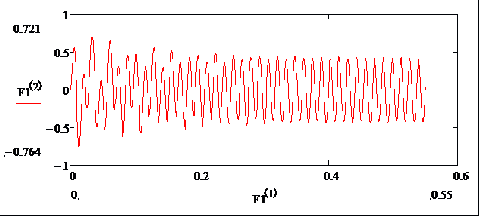
Рисунок А.7 Зависимость тока i 1 от времени.
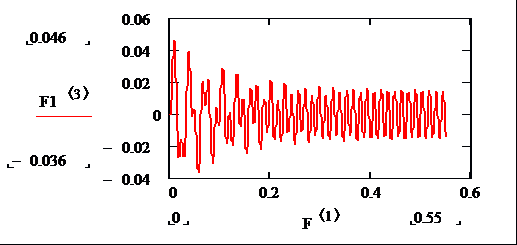
Рисунок А.8 Зависимость тока i 2 от времени.
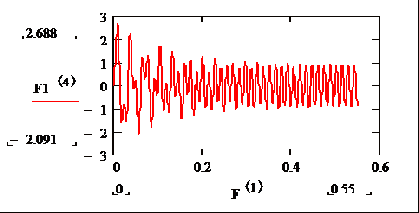
Рисунок А.9 Зависимость напряжения Uc на конденсаторе от времени.
3.2 Описание исследований
Исследуем влияние индуктивности L 1 на минимальное значение напряжения на конденсаторе. Для этого изменяем варьируемый параметр L 1 от 0.026 до 0.045 решаем дифференциальное уравнение с помощью функции rkfixed . По каждому из проведённых опытов, в зависимости от значения варьируемой индуктивности L 1, построили графики зависимостей токов и напряжений от времени.
Таблица 3.2.1 — Значения варьируемого параметра L 1
На примере рассмотрим 1 опыт. Решаем дифференциальное уравнение с помощью функции rkfixed . Берём L 1=0.026Гн. Строим график зависимости напряжения от времени.
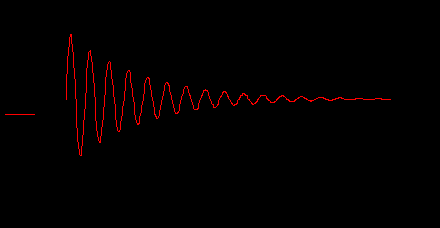
Рисунок А.10 — График зависимости напряжения от времени
Остальные 5 опытов проводим аналогично, для каждого значения L 1. Затем получившиеся графики функций напряжения на конденсаторе строим на одном поле:
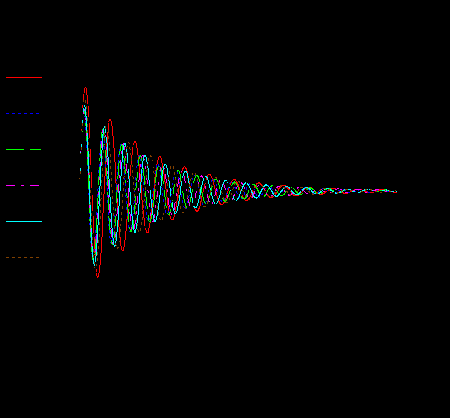
Рисунок А.11-Сводный график зависимости напряжения от времени
Сохраняем полученные результаты в файлы данных по примеру опыта 1 с помощью функции:

В остальных 5 опытах полученные результаты сохраняем в файлы данных аналогично. (Приложение А)
3.3 Описание реализации базовой модели в Scilab
Считываем файлы данных полученных в п.1.3.Для считывания данных Mathad используем функцию read . Функция read предназначена для чтения файлов данных в памяти Scilab . В данной курсовой работе имеют место следующие обозначения и параметры: А-матрица, размерность которой (-1,1) в которой «:»-означает все строки, а число 1-обозначает первый столбец.Т-матрица времени, размерностью (-1,1).
« r 111. dat «-Имя файла данных.
A (:,1)= read (« r 111. dat «,-1,1)- пример считывания файла данных.
Аналогично считываем другие файлы данных. (Приложение Б)
Функция Figure предназначена для создания графического окна.
Для построения графика зависимости минимумов напряжений от индуктивности используем функцию plot ( T , A )(Рисунок Б.1)
3.4 Описание исследований в Scilab
Для выполнения аппроксимации зависимости минимумов напряжений от индуктивности создаем графическое окно(2).
Задаем вектор варьируемого параметра L . Для поиска минимумов напряжений создаем цикл с предусловием в котором используется стандартная функция работы с матрицами min .
for i=1:6(i)=min(A(:,i))
End
Находим значения аппроксимирующей функции(Рисунок Б.2)
Задаем столбец начальных значений для коэффициента аппроксимирующей функции. С помощью команды datafit (метод наименьших квадратов)осуществляется параметрическое приближение экспериментальных данных к функции зависимости минимумов напряжений от индуктивности.
deff(‘[A]=F(k,x)’,’A=x(2)-(k(1)*x(1)^2+k(2)*x(1)+k(3))’)=[0.026 0.028 0.03 0.035 0.04 0.045]=[0;0;0]
[k,s]=datafit(F,[L;MIN],nach)(k)=0.026:0.001:0.045=k(1).*(X.^2)+k(2).*X+k(3)
Погрешность составила 3.034E-9.Для данной зависимости подобрана функция:
Y = k (1).*( X .^2)+ k (2).* X + k (3)
Строим график исходной и аппроксимирующей функций. (Рисунок Б.3,Рисунок Б.4)
Для функции тока i 2, полученной в п.1.1, вычисляем время, при котором ток достигает порогового значения, равного -0.005. Для этого задаем переменной v значение времени Т, а переменной О значение тока i 2.
Далее составляем программный фрагмент в котором находим время при котором ток достигает порогового значения, равного -0.005.
v=T=D(:,1)=1O(i)>-0.005=i+1=i-1(v(nom))
Даем графическую интерпретацию результата.(Рисунок Б.5)
3.5 Вывод по результатам исследований
При выполнении курсовой работы с помощью СКМ Mathcad были вычислены значения функций напряжения на конденсаторе без учета гармонического воздействия U ( t ) и с учетом гармонического воздействия U ( t ) при помощи функции rkfixed . Была получена зависимость минимального значения напряжения на конденсаторе от значения индуктивности L 1, которое изменялось от 0.026 до 0.045 Гн.Были построены графики зависимостей U ( t )с учетом гармонического воздействия и без него.
Также был построен сводный график зависимости минимального значения напряжения на конденсаторе от значения индуктивности L 1=0.026…0.045 Гн.
В СКМ Scilab при помощи программного фрагмента были найдены минимумы напряжений. После чего был построен график зависимости минимумов напряжений от индуктивности. Была выполнена аппроксимация зависимости минимумов напряжений от индуктивности с помощью подобранной функции Y = k (1).*( X .^2)+ k (2).* X + k (3).
Погрешность составила 3.034E-9. Далее с помощью программного фрагмента было найдено время, при котором ток i 2 достигает порогового значения, равного -0.005. Данное значение равно 0.02035с.Для наглядности даем графическую интерпретацию результата.
Заключение
В данной курсовой работе был произведён анализ электрических процессов в цепи второго порядка с использованием систем компьютерной математики MathCAD и Scilab .
Использование систем компьютерной математики позволило с высокой точностью проанализировать электрические процессы, происходящие в цепях второго порядка.
Математическое моделирование в сочетании с применением новейших компьютерных технологий значительно облегчает сложнейшие математические вычисления. Именно поэтому разработка СКМ и их совершенствование непрерывно идет в ногу со временем. Ведь расчеты становятся все объёмнее, и человеку становится все труднее справляться с ними.
В данной курсовой работе был произведён анализ и исследование электрических процессов в цепи второго порядка. С использованием систем компьютерной математики MathCAD и Scilab было исследовано влияние величины индуктивности на минимальное значение напряжения на конденсаторе, а также осуществлено параметрическое приближение экспериментальных данных к функции зависимости минимумов напряжений от индуктивности. Для функции тока i 2 было вычислено время при котором он достигал пороговое значение -0.005с.
Список использованных источников
[Электронный ресурс]//URL: https://drprom.ru/kursovaya/po-sistemam-avtomaticheskogo-upravleniya-scilab/
1. Майер Р.В. Расчет электрических целей в системе MathCAD : Учебное пособие. — Глазов: ГГПИ, 2007, — 44 с.
. Дьяконов А. А. Справочник по MathCAD 2000. М.: Ск — пресс, 2000.-352с.
3.Зарубин В.С. Математическое моделирование в технике: Учеб, для вузов / Под ред. В.С. Зарубина, А.П. Крищенко. — 2-е изд., стереотип. — М.: Изд. МГТУ им. Н.Э. Баумана, 2003. -496 с.
4.
5.Турчак Л. И.. Основы численных методов: Учеб. пособие.- М.: Наука Гл. ред. физ.-мат. лит., 1987.- 320 с.
