Анализ метрологических характеристик

метки: Заключение, Работа, Метрология, Курсовой, Выборка, Измерение, Закон, Гипотеза

Магнитоэлектрический датчик Холла получил свое название по имени Э.Холла, американского физика, открывшего в 1879 г. важное гальваномагнитное явление. Бесконтактные клавишные переключатели на основе эффекта Холла применялись за рубежом довольно широко уже с начала 70-х годов. Достоинства этого переключателя — высокая надежность и долговечность, малые габариты, а недостатки — постоянное потребление энергии и сравнительно высокая стоимость.

Если на полупроводник, по которому (вдоль) протекает ток, воздействовать магнитным полем, то в нем возникает поперечная разность потенциалов (ЭДС Холла).

Возникающая поперечная ЭДС может иметь напряжение только на 3 В меньше, чем напряжение питания.

Рассмотрим полупроводниковую пластинку размером 5х5 мм (см. рис., поз.а).

Если по пластинке между двумя параллельными сторонами пропустить ток и одновременно поднести к ней постоянный магнит, а к двум другим сторонам квадрата подсоединить провода, то получим генератор Холла (рис., поз.б).

Если между магнитом и полупроводником поместить перемещающийся экран с прорезями, получим импульсный генератор Холла.

Принцип действия генератора Холла:

• а — нет магнитного поля, по полупроводнику протекает ток питания — АВ;
• б — под действием магнитного поля — Н появляется ЭДС Холла — ЕF;
• в — датчик Холла

Датчик Холла имеет щелевую конструкцию. С одной стороны щели расположен полупроводник, по которому при включенном зажигании протекает ток, а с другой стороны — постоянный магнит. В щель датчика входит стальной цилиндрический экран с прорезями. При вращении экрана, когда его прорези оказываются в щели датчика, магнитный поток воздействует на полупроводник с протекающим по нему током и управляющие импульсы датчика Холла подаются в коммутатор, в котором они преобразуются в импульсы тока в первичной обмотке катушки зажигания.

Проверку датчика Холла проще всего производить заменой на заведомо исправный, но можно воспользоваться и обыкновенным вольтметром (тестером).

У исправного датчика Холла вольтметр, включенный на измерения постоянного напряжения и подключенный к выходу датчика, по мере вращения вала датчика-распределителя должен резко менять показания от примерно 0,4В до величины, не более чем на 3 В отличающейся от напряжения питания.

Схема изделия, состав, принцип действия

В цехе выпускается изделие – средство измерения, состоящее из следующих частей:

Датчики тока и напряжения

... напряжения. Также напряжение можно измерить датчиками напряжения, основанные на эффекте Холла. Схематическое изображение измерения напряжения датчиком Холла замкнутого типа представлено на рисунке 7. , Рисунок 7 - Измерение напряжения датчиком Холла замкнутого типа Это тот же датчик тока Холла, ...

• Д- первичный датчик (покупное изделие);
• У- масштабирующий усилитель (изготавливаемое изделие);
• АЦП- анологово – цифровой преобразователь (покупное изделие);
• ЦОУ- цифровое отсчётное устройство;
• ИСН- источник стабилизированного напряжения. Сигналы: Х- входная измеряемая величина, Uд — напряжение на выходе первичного датчика;
• Uу- напряжение на выходе усилителя;
• Uп- цифровой сигнал на выходе АЦП.

За смену выпускается партия изделий. Во время смены случайным образом отбирают n изделий и проводят их комплексные испытания, по результатам которых определяют метрологические характеристики и делают заключение о качестве изделия и технологического процесса.

Коэффициент усиления для масштабирующего усилителя определяется по результатам испытаний. Точное значение к _у с допустимой погрешностью m_к ±Dк. Однако из – за несовершенства оборудования технологии изготовления, ошибок персонала, к_у принимает статистический разброс. Теоретически установлено, значение выходного напряжения у датчика и усилителя распределено по нормальному закону со среднеквадратическим отклонением (СКО) s_к .

У датчика измеряется максимальное выходное напряжение U _д , значение которого теоретически распределено по нормальному закону с математическим ожиданием m_д и погрешностью в виде СКО s_д. Для аналого – цифрового преобразователя напряжения закон распределения погрешности треугольный (Симпсона) при максимальном её значении D_{m .}

Поскольку в процессе производства изнашивается оборудование или оно настраивается и обслуживается недостаточно квалифицированно, меняется исходное сырьё и параметры приобретаемых элементов, то указанные статистические параметры «уходят». Их уход необходимо устранить подстройкой оборудования – внести коррекцию. Это в наибольшей мере касается масштабирующего усилителя. Для определения необходимости подстройки оборудования используют две выборки изделий, полученные в разное время. Оценки основных параметров, найденные из этих выборок, определяются как m _к1 ^* =к₁ * m^* _к , s^* _к1 =к₁ *s_к ^* и m_к2 ^* =к₂ * m^* _к , s^* _к2 =к₂ *s_к ^* , где к₁ и к₂ – поправочные коэффициенты, задаваемые для определения оценок.

Генерация выборок

Описание методов генерации выборок

Совокупность всех случайных величин называется генеральной совокупностью. При измерениях генеральная совокупность – непрерывная случайная величина, характеризуемая каким законом распределения. Множество значений случайной величины, полученное в результате наблюдения над нею, называется случайной выборкой. Выборка – конечное множество измерений, взятых из генеральной совокупности случайным образом.

Полным описанием случайной величины и погрешности является её закон распределения:

1) Нормальный закон распределения (закон Гаусса) является одним из наиболее распространённых законов распределения. Объясняется это тем, что во многих случаях погрешность измерения образуется под действием большой совокупности различных, независимых друг от друга причин. На основании центральной предельной теоремы теории вероятностей результатом действия этих причин будет погрешность, распределённая по нормальному закону при условии, что ни одна из этих причин не является существенно преобладающей.

Генераторы и усилители СВЧ-сигналов

... либо настроить клистрон в режим генерации, либо сорвать генерацию. Это осуществляется изменением напряжения на ... - отражатель; 5 - резонатор; 6 - вывод энергии генератора. Другим вариантом клистронов, является отражательный клистрон, схематически изображенный на ... приборов СВЧ, использующих резонансные колебательные системы. Важными преимуществами ламп бегущей волны как усилителей является ...

Генерирование выборки по нормальному закону:

a=normrnd(m _x ,s,m,n) – где m_x — математическое ожидание; s — оценка среднеквадратического отклонения (дисперсии); m – число – число столбцов.

2) Равномерный закон распределения. Если погрешность измерений с одинаковой вероятностью может принимать любые значения, не выходящие за некоторые границы, то такая погрешность описывается равномерным законом распределения.

Генерация выборки по равномерному закону:

• с=unifrnd(a,b,m,n) – где a…b – интервал;
• m – число – число столбцов.

Приведение выборок

1. Генерация выборки для датчика.

Закон распределения погрешности — нормальный

математическое ожидание m _д =0,05

среднеквадратическое отклонение s _д =0,001

объем выборки n=100

Полученная выборка:

a =

0.0496 0.0483 0.0501 0.0503 0.0489 0.0512 0.0512

0.0500 0.0503 0.0502 0.0498 0.0507 0.0494 0.0522

0.0499 0.0501 0.0511 0.0501 0.0499 0.0492 0.0503

0.0487 0.0507 0.0516 0.0493 0.0509 0.0513 0.0484

0.0486 0.0506 0.0496 0.0507 0.0508 0.0507 0.0513

0.0507 0.0512 0.0488 0.0500 0.0498 0.0484 0.0503

0.0489 0.0514 0.0492 0.0505 0.0502 0.0491 0.0478

0.0499 0.0490 0.0506 0.0505 0.0517 0.0506 0.0494

0.0504 0.0490 0.0500 0.0500 0.0500 0.0497 0.0511

0.0481 0.0504 0.0509 0.0507 0.0506 0.0500 0.0507

0.0506 0.0497 0.0496 0.0497 0.0485 0.0498 0.0501

0.0503 0.0514 0.0496 0.0506 0.0508 0.0509 0.0490

0.0502 0.0502 0.0490 0.0493 0.0511 0.0499 0.0504

0.0501 0.0494 0.0494 0.0504 0.0491 0.0508 0.0506

0.0492 0.0497

1. Генерация выборки для усилителя

Закон распределения погрешности — нормальный

математическое ожидание m _к =200

среднеквадратическое отклонение s _к =0,9

объем выборки n=100

Полученная выборка:

b =

198.9310 198.0179 200.8877 199.5332 200.2946 200.2107 200.0193

199.0964 199.1476 199.6630 198.9327 199.0497 201.3252 200.0502

198.9044 199.9629 198.9845 198.7857 199.7650 200.8581 200.1158

200.5908 198.9490 199.5855 199.7638 198.9082 198.8125 200.8381

200.0101 199.4194 200.7252 200.2085 199.1092 201.2056 200.2606

201.3310 201.0242 199.3843 198.8373 199.9344 199.7025 199.2407

200.4480 201.3396 199.5082 199.2379 199.7783 200.5967 199.2312

198.9188 199.8921 199.9412 200.4368 199.4641 199.8653 199.6087

199.9286 201.3816 199.4542 198.7874 200.4224 199.1868 200.0323

199.4352 200.4819 200.4976 199.8167 198.1511 200.1193 201.4336

200.9166 198.5776 199.9292 199.3865 199.0779 198.8891 200.2599

199.6136 200.0502 199.6689 199.5815 200.3339 200.6555 201.9009

198.7784 199.0797 200.9341 199.6492 198.7569 200.2840 201.3979

200.6371 201.7616 200.4541 201.6781 199.6942 198.9742 199.8100

201.712 198.9954

1. Генерация выборки для аналого – цифрового преобразователя (АЦП)

Закон распределения погрешности — равномерный

Границы интервала выборки D _m от –0.02 до 0.02

объем выборки n=100

Полученная выборка

C =

0.0180 -0.0108 0.0043 -0.0006 0.0157 0.0105 -0.0017

• 0.0193 0.0129 -0.0022 0.0046 0.0117 0.0169 0.0095
• 0.0129 -0.0038 0.0174 0.0167 -0.0036 0.0157 -0.0177
• 0.0059 0.0125 -0.0196 -0.0144 -0.0119 -0.0121 0.0042
• 0.0091 -0.0120 -0.0194 0.0099 -0.0022 0.0173 -0.0014
• 0.0033 0.0138 0.0010 -0.0119 0.0069 0.0135 -0.0192

0.0073 -0.0048 0.0133 0.0001 0.0084 -0.0028 -0.0078

• 0.0124 -0.0123 0.0073 -0.0079 0.0017 -0.0140 0.0079
• 0.0049 0.0144 0.0141 0.0037 -0.0001 0.0160 0.0129

0.0058 0.0127 0.0064 -0.0063 -0.0084 -0.0064 0.0014

0.0091 -0.0076 0.0135 0.0027 -0.0052 0.0081 0.0019

• 0.0022 0.0078 0.0049 0.0118 0.0183 0.0009 0.0152
• 0.0131 0.0192 -0.0091 -0.0099 0.0150 0.0095 -0.0145
• 0.0195 0.0158 -0.0120 -0.0081 0.0065 -0.0086 -0.0012
• 0.0174 0.0195

Первичная обработка результатов измерений

К первичной обработке результатов наблюдений относят такие операции как сортировка и уплотнение данных, обработка грубых, аномальных результатов и определение эмпирической функции распределения.

Расчёт с помощью метода моментов оценок математического ожидания и дисперсии

Оценка находится путём приравнивания моментов генеральной совокупности соответствующим выборочным моментам, полученным из эксперимента. Этот метод даёт состоятельные оценки, точность которых возрастает с увеличением числа измерений.

Оценка математического ожидания:

где n – число измерений; x – случайная величина.

Оценка дисперсии:

Оценка математического ожидания для выборки случайных величин датчика:

Полученная оценка математического ожидания

m1 = 0.0499

Оценка математического ожидания для выборки случайных величин усилителя:

Полученная оценка математического ожидания

m2 = 199.9391

Оценка математического ожидания для выборки случайных величин АЦП:

Полученная оценка математического ожидания

m3 = 0.0012

Оценка дисперсии для выборки случайных величин датчика:

Полученная оценка дисперсии

sigma = 0.00096

Оценка дисперсии для выборки случайных величин усилителя:

Полученная оценка дисперсии

sigmb = 0.8756

Оценка дисперсии для выборки случайных величин АЦП:

Полученная оценка дисперсии

sigmc = 0.0108

Анализ наличия результатов, которые содержат грубые погрешности или промахи:

Обработка грубых, аномальных результатов проводится с целью исключения их из дальнейшей выборки. Если один-два результата резко отличаются от остальных, то следует прежде всего проверить, не являются ли они промахами. Если это не обнаружено то необходимо подвергнуть результаты статистическому анализу.

Преобразование выборок в вариационные ряды

1) Сортировка данных заключается в построении упорядоченного (вариационного) ряда, в котором результаты измерений расположены в порядке возрастания(x ₁ 2<�…n).

2) Определяем оценку математического ожидания m _x и оценку среднеквадратического отклонения S_x .

3) Для сомнительного результата x _i вычисляют критерий Стьюдента:

где t – критерий Стьюдента; x_i – сомнительный результат.

4) По таблице находят значение интеграла вероятности (функции Лапласа) Ф(t);

5) Вычисляют a=1-P _д =1-0,99=0,01 где P_д – доверительный интервал;

• a — уровень значимости.

6) Если неравенство 1-2*Ф(t)

Переход к интервальным рядам

гистограммы, полигона и эмпирической функции распределения

Для определения эмпирического закона распределения от вариационного ряда нужно перейти к статистическому (интервальному) ряду. Для этого вариационный ряд необходимо разбить на N интервалов.

гистограммы, полигона для выборки датчика

Разобьём выборку на 10 интервалов. Количество результатов попавших в каждый интервал (n _i ):

4 3 5 13 16 20 17 10 6 6

Длина интервала (I):

I=(I _max -I_min )/ N, где I_max — максимальное значение выборки, I_min — минимальное значение выборки, N- количество интервалов

I=(0.0518-0.0474)/10=0.00044

Для каждого интервала подсчитываем частости:

, где n_i – число результатов в i-ом интервале; n – общее кол-во результатов в выборке.

От частостей переходим к эмпирической плотности вероятности:

, где I_i — длина интервала;

Эмпирическая функция распределения рассчитывается по формуле:

n i	4	3	5	13	16	20	17	10	6	6
P i *	0.04	0.03	0.05	0.13	0.16	0.20	0.17	0.10	0.06	0.06
f i *	91.10	68.33	113.88	296.09	364.42	455.53	387.20	227.76	136.66	136.66
F i *	0.04	0.07	0.12	0.25	0.41	0.61	0.78	0.88	0.94	1.00

Полученные гистограммы:

Гистограмма и полигон эмпирической плотности распределения датчика:

Гистограмма эмпирической функции распределения для датчика:

гистограммы и полигона для выборки усилителя

Разобьём выборку на 10 интервалов. Количество результатов попавших в интервал (n _i ):

1 3 14 11 18 20 16 9 5 1

Длина интервала (I):

I=(I _max -I_min )/ N, где I_max — максимальное значение выборки, I_min — минимальное значение выборки, N- количество интервалов

I=(202.01-197.83)/10=0.4186

Для каждого интервала подсчитываем частости:

, где n_i – число результатов в i-ом интервале; n – общее кол-во результатов в выборке.

От частостей переходим к эмпирической плотности вероятности:

, где I_i — длина интервала;

Эмпирическая функция распределения рассчитывается по формуле:

;

n i	1	3	14	11	18	20	16	9	5	1
P i *	0.01	0.03	0.14	0.11	0.18	0.20	0.16	0.09	0.05	0.01
f i *	0.024	0.073	0.341	0.268	0.438	0.487	0.390	0.219	0.121	0.024
F i *	0.01	0.04	0.18	0.29	0.47	0.68	0.84	0.93	0.98	1.00

Полученные гистограммы:

Гистограмма и полигон эмпирической плотности распределения для усилителя.

Гистограмма эмпирической функции распределения для усилителя:

гистограммы и полигона для выборки АЦП.

Разобьём выборку на 10 интервалов. Количество результатов попавших в интервал (n _i ):

6 11 4 13 14 8 15 8 11 10

Длина интервала (I):

I=(I _max -I_min )/ N, где I_max — максимальное значение выборки, I_min — минимальное значение выборки, N- количество интервалов

I=(0.0197+.00199)/10= 0.0040

Для каждого интервала подсчитываем частости:

, где n_i – число результатов в i-ом интервале; n – общее кол-во результатов в выборке.

От частостей переходим к эмпирической плотности вероятности:

, где I_i — длина интервала;

Эмпирическая функция распределения рассчитывается по формуле:

;

n i	6	11	4	13	14	8	15	8	11	10
P i *	0.06	0.11	0.04	0.13	0.14	0.08	0.15	0.08	0.11	0.10
f i *	15.09	27.66	10.06	32.70	35.21	20.12	37.73	20.12	27.66	25.15
F i *	0.06	0.17	0.21	0.34	0.48	0.56	0.71	0.79	0.90	1.00

Полученные гистограммы:

Гистограмма и полигон эмпирической плотности распределения для АЦП

Гистограмма эмпирической функции распределения для АЦП:

Определение интервальных оценок первых двух выборок при заданной доверительной вероятности Р д .

Интервальным или доверительным оцениванием называют оценивание, при котором по данным выборки определяют интервал, накрывающий истинное значение оцениваемого параметра с заданной вероятностью. Интервальное оценивание особенно необходимо при малом объёме выборки, когда точечная оценка мало надёжна.

Интервальная оценка для математического ожидания может быть представлена в виде:

(m ^* _x -e)x< (m^* _x +e) или ? m^* _x — m_x ?_g =( m^* _x -e, m^* _x +e) , определяющий область возможных значений m^* _x , которая с вероятностью Р(?m^* _x — m_x ?_x , называется доверительным интервалом, а вероятность Р=g — доверительной вероятностью.

Определение интервальных оценок при заданной доверительной вероятности Р _д для датчика:

Доверительная вероятность

Р _д =g=0,99

к= n-1=100-1=99

Значение величины t _{g k} при известной доверительной вероятности g=0,99 и к=99 находим по таблице:

S _x =0,00096, t_{g k} = 2,63, по известной величине t_{g k} находим искомую величину e

e=( t _{g k *} S_x )/?n=(2,63*0,00096)/?100 =0,00025

Результат измерения с погрешностью:

D _s =0,05000±0,00025 с Р_д =0,99

Определение интервальных оценок при заданной доверительной вероятности Р _д для усилителя:

Аналогично предыдущему пункту находим значение величины t _{g k} и искомую величину e

Доверительная вероятность

Р _д =g=0,99

к= n-1

t _{g k} = 2,63, S_x =0,8756

e=( t _{g k *} S_x )/?n=(2,63*0,8756)/ ?100=0,2156

Результат измерения с погрешностью:

U _s =200,00±0,22 с Р_д =0,99

Проверка гипотезы о равенстве точности измерений

Проверка производится для второй выборки и для её двух разновидностей, заданных через коэффициенты к ₁ и к_2. Такая задача обычно возникает в измерениях одной и той же величины разными приборами или же при проведении серий измерений одним и тем же прибором, но в различных условиях.

H ₀ : s1=s2;

H ₁ : s1?s2;

Первая разновидность выборки, задаётся через коэффициент к ₁ =1.02

m _{x 1} = к₁ *m_x ==203.94

=0.6989

Вторая разновидность выборки, задаётся через коэффициент к ₂ =1.1

m _{x 2} = к₂ *m_x ==219.93

=0.8128

Оценка дисперсии для усилителя: S ² _x = 0.6718

Для проверки исходной гипотезы используется односторонний критерий Фишера: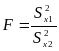

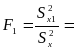1.0404, затем находим по таблице F(a)=1.00

F ₁ > F(a) – принимается гипотеза Н₁ , о том что у двух выборок разная оценка дисперсии.

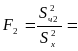1.2100, затем находим по таблице F(a)=1.00

F ₂ > F(a) – принимается гипотеза Н₁ , о том что у двух выборок разная оценка дисперсии.

Проверка гипотезы о равенстве средних

Имеется две выборки результатов измерений одной и той же величины. Оценки математических ожиданий, полученные по выборкам m _{x 1} и m_{x 2} . Требуется проверить гипотезу Н₀ : m_{x 1} = m_{x 2} относительно гипотезы Н₁ : m_{x 1} ? m_{x 2} . Если гипотеза Н₀ будет принята, то можно считать, что отличия в значениях m_{x 1} и m_{x 2} обусловлены случайными причинами и обе выборки далее можно использовать совместно. Если же будет принята гипотеза Н₁ , то различия в значениях m_{x 1} и m_{x 2} будут свидетельствовать о существенных различиях в условиях эксперимента – выборки нельзя далее использовать совместно.

1) Проверка гипотезы о равенстве средних для первой разновидности выборки, заданной через коэффициент к ₁ =1.02.

Находим значение двустороннего критерия Стьюдента

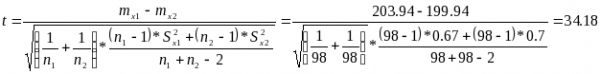
Уровень значимости a=0.01;

Число степеней свободы k=n ₁ +n₂ -2;

По таблице находим t _{a , k} =2.63;

• t >
• t _{a , k} — принимается гипотеза Н₁ , о том, что у двух выборок различная оценка математического ожидания.

2) Проверка гипотезы о равенстве средних для второй разновидности выборки, заданной через коэффициент к ₂ =1.1.

Находим значение двустороннего критерия Стьюдента

Уровень значимости a=0.01;

Число степеней свободы k=n ₁ +n₂ -2;

По таблице находим t _{a , k} =2.63;

• t >
• t _{a , k} — принимается гипотеза Н₁ , о том, что у двух выборок различная оценка математического ожидания.

3) Проверка гипотезы для усилителя о соответствии измеренного значения m _x требованиям технического задания (ТЗ).

Проверяется гипотеза Н ₀ : m_x =a, относительно гипотезы Н1: m_x ? a, где а – требования ТЗ. Для требований ТЗ полагают n₂ =? и получают критерий в виде:

t < t _{a , k} — принимается гипотеза Н₀ , о том что измеренное значение m_x соответствует требованиям ТЗ(m_x =a).

4) Проверка гипотезы о соответствии измеренного значения m _x требованиям ТЗ для первой разновидности выборки, заданной через к₁ =1.02.

t > t _{a , k} — принимается гипотеза Н₁ , что свидетельствует о несоответствии измеренного значения m_{x 1} требованиям ТЗ (m_{x 1} ? а).

5) Проверка гипотезы о соответствии измеренного значения m _x требованиям ТЗ для второй разновидности выборки, заданной через к₂ =1.1.

t > t _{a , k} — принимается гипотеза Н₁ , что свидетельствует о несоответствии измеренного значения m_{x 2} требованиям ТЗ (m_{x 2} ? а).

Гипотезы о тождественности эмпирического и теоретического законов для всех трёх выборок

Критерий Пирсона c 2

1) Проверка гипотезы о тождественности эмпирического и теоретического законов по критерию Пирсона c ² для датчика:

Н ₀ : нормальный закон

Н ₁ : ненормальный закон

Используем те же интервалы, что и при построении гистограмм, но учитывая то, чтобы в интервалах было не менее пяти результатов. Если интервал содержит менее пяти значений его объединяют с соседним. В нашем случае объединяется 1-ый и 2-ой интервалы. (N=9)

4 3 5 13 16 20 17 10 6 6

7 5 13 16 20 17 10 6 6

Теоретические вероятности попадания результатов в интервалы находим по формуле: 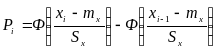, где xi-1 – начало; xi – конец i-го интервала;

Определяем теоретическое число результатов в каждом интервале: n _iT =n*P_i ;

0.0475 0.0484 0.0488 0.0492 0.0497 0.0501 0.0506 0.0510 0.0514 0.0519

I	1	2	3	4	5	6	7	8	9
n i	7	5	13	16	20	17	10	6	6
P i	0.0487	0.0601	0.0963	0.1693	0.1570	0.1855	0.1158	0.0785	0.0528
n iT	4.87	6.01	9.63	16.92	15.69	18.55	11.58	7.84	5.28

Вычисляем критерий согласия c ² :

a=0.01;

— По выборке определяется два параметра предполагаемого распределения: математическое ожидание и среднеквадратическое отклонение, значит r=2 и число степеней свободы k=N-r-1=9-2-1=6. Для этих значений a и k находим критическое значение по таблице: c ² _{a , k} =15.0

c ² 2_{a , k} ? При данном уровне значимости принимается исходная гипотеза Н₀ , что свидетельствует о распределении случайной величины по нормальному закону.

2) Проверка гипотезы о тождественности эмпирического и теоретического законов по критерию Пирсона c ² для усилителя:

Н ₀ : нормальный закон

Н ₁ : ненормальный закон

I	1	2	3	4	5	6	7
n i	18	11	18	20	16	9	6
P i	0.1638	0.1494	0.2143	0.2715	0.1701	0.0646	0.0561
n iT	16.37	14.93	21.42	27.15	17.01	6.46	5.60

c ² =8.85 c² _{a ,k} =11.7

c ² 2_{a , k} ? При данном уровне значимости принимается исходная гипотеза Н₀ , что свидетельствует о распределении случайной величины по нормальному закону.

3) Проверка гипотезы о тождественности эмпирического и теоретического законов по критерию Пирсона c ² для АЦП:

Н ₀ : равномерный закон

Н ₁ : неравномерный закон

Dm=0.02

Закон равномерного распределения записывается в виде:

при -Dm ? D ? Dm

при -Dm > D > Dm

Вероятность появления погрешности в интервале равна:

i	1	2	3	4	5	6	7	8	9	10
P i	0.097	0.097	0.097	0.097	0.097	0.097	0.097	0.097	0.097	0.097
n iT	9.7	9.7	9.7	9.7	9.7	9.7	9.7	9.7	9.7	9.7

c ² =5.05 k=10-0-1=9 c² _{a ,k} =19.7

c ² 2_{a , k} ? При данном уровне значимости принимается исходная гипотеза Н₀ , что свидетельствует о распределении случайной величины по равномерному закону.

Критерий Колмогорова

1) Гипотеза о тождественности эмпирического и теоретического законов по критерию Колмогорова для датчика.

F i *	0.04	0.07	0.12	0.25	0.41	0.61	0.78	0.88	0.94	1.00
F i	0.02	0.055	0.095	0.185	0.33	0.51	0.695	0.83	0.91	0.97
F i * — Fi	0.02	0.015	0.025	0.065	0.08	0.1	0.085	0.05	0.03	0.03

Н ₀ : нормальный закон

Н ₁ : ненормальный закон

Находим максимальную разность F _i ^* — F_i

D=max| F _i ^* — F_i |=0.1

l=D?N=0.1*3=0.3

a=0.01 ? l _a =1.63

la ? При данном уровне значимости принимается исходная гипотеза Н ₀ , что свидетельствует о распределении случайной величины по нормальному закону.

2) Гипотеза о тождественности эмпирического и теоретического законов по критерию Колмогорова для усилителя.

F i *	0.01	0.04	0.18	0.29	0.47	0.68	0.84	0.93	0.98	1.00
F i	0.005	0.025	0.11	0.235	0.38	0.575	0.76	0.885	0.955	0.99
F i * — Fi	0.005	0.015	0.07	0.055	0.09	0.105	0.08	0.045	0.025	0.01

Н ₀ : нормальный закон

Н ₁ : ненормальный закон

Находим максимальную разность F _i ^* — F_i

D=max| F _i ^* — F_i |=0.105

l=D?N=0.105*2.64=0.27

a=0.01 ? l _a =1.63

la ? При данном уровне значимости принимается исходная гипотеза Н ₀ , что свидетельствует о распределении случайной величины по нормальному закону.

3) Гипотеза о тождественности эмпирического и теоретического законов по критерию Колмогорова для АЦП.

F i *	0.06	0.17	0.21	0.34	0.48	0.56	0.71	0.79	0.90	1.00
F i	0.03	0.115	0.19	0.275	0.43	0.52	0.635	0.75	0.845	0.95
F i * — Fi	0.03	0.05	0.02	0.065	0.05	0.04	0.075	0.04	0.055	0.05

Н ₀ : равномерный закон

Н ₁ : неравномерный закон

Находим максимальную разность F _i ^* — F_i

D=max| F _i ^* — F_i |=0.075

l=D?N=0.075*3=0.22

a=0.01 ? l _a =1.63

la ? При данном уровне значимости принимается исходная гипотеза Н ₀ , что свидетельствует о распределении случайной величины по равномерному закону.

Нахождение процента выхода годных для изделий по результатам обработки второй выборки

U _s =200,00±0,22 с Р_д =0,99

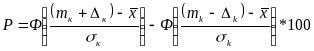
По таблице функций Лапласа находим Ф(Z)

По результатам обработки второй выборки процент выхода годных получился равным %.

Расчет суммарной погрешности измерения

Если связь между частными погрешностями слабая (вызвана независимыми причинами или источниками), то принимают r _ij =0. При этом погрешности измеряются геометрически.

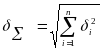
Выражение случайных погрешностей в относительных значениях:

%

%

s=Dm/?3=0.02/1.7=0.012

%

Суммарная погрешность d _? =1.2%

Выводы

Контроль качества продукции, вследствие ошибок, осуществляется с помощью наблюдений. Наблюдение над исследуемой величиной может осуществляться по-разному: путём зрительного или слухового восприятия, путём подсчёта числа событий, характеризующих состояние исследуемой величины и, наконец, путём измерения её. Осуществляя измерение, мы измеряем исследуемую величину, т.е. определяем некоторое приближённое её значение и устанавливаем с какой точностью проведено измерение, вычисляем степень близости этого приближённого значения к действительному. Если точность недостаточна, то необходимо принять меры к её повышению и измерения повторить. Вследствие погрешностей, присущих любому измерению, результат отдельного измерения x _i случаен. Поэтому для выявления действительного значения измеряемой величины необходимо произвести серию измерений. Результаты измерений x_i предстают в виде случайной величины x. Значит по результатам измерений, измеряемую величину можно характеризовать только вероятностными характеристиками, которые могут быть установлены лишь в результате статистической обработки результатов измерений.

Поэтому цель нашей работы заключается в статистическом анализе качества, определении метрологических характеристик изделия методом имитационного моделирования, проверки ошибок ОТК, погрешностей, гипотез, и сделать заключение о качестве изделия и о качестве технологического процесса.

Литература

[Электронный ресурс]//URL: https://drprom.ru/kursovaya/zaklyuchenie-dlya-kursovoy-rabotyi-po-metrologii/

1. Электрорадиоизмерения и обработка результатов измерений: Учебное пособие/Под ред. В.Г. Глаголевского; ЛИАП. Л., 1987.

1. Справочник по преобразовательной технике/ Под ред. И.М. Чиженко. Киев: Техника, 1978.

1. Руденко В.С., Сенько В.И., Чиженко И.М. Основы преобразовательной техники. М.: Высш. шк., 1980.

Явление термоэлектричества, открытое в начале 20-го века русским академиком Эпинусом, заключается в следующем. Если в цепи, состоящей из 2-х различных проводников, соединенных между собой в точках 1 и 2, нагревать одну из этих точек соединения, то в цепи появится Э.Д.С., называется термоэлектродвижущей силой и являющаяся разностью функций температур, мест соединения проводников.

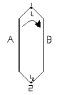
Подобная термоэлектрическая цепь, составленная из двух проводников (термоэлектродов), называется термопарой. Точки соединения называют рабочим и свободным концами термопары.

Таким образом, изменение температуры рассматриваемым методом сводится к измерению Э.Д.С., которую термопара развивает при строго постоянной температуре t ₂ свободного конца.

пирометра.