Инерционное звено второго порядка

метки: Порядок, Второе, Инерционный, Звено, Система, Уравнение, Процесс, Автоматический

Инерционное звено второго порядка — раздел Философия, Автоматическое управление пуском и остановкой оборудования, коммутационные операции и т.д. Уравнение Динамики Звена …

Уравнение динамики звена

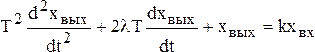, (4.20)

где Т –постоянная времени, коэффициент демпфирования, коэффициент передачи звена.

Операторное уравнение и передаточная функция звена следующие:

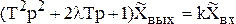, (4.21)

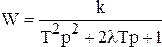. (4.22)

Отличительной чертой этого звена является возможность существования трех видов переходных характеристик, что определяется корнями его характеристического уравнения 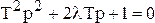. Корни этого уравнения

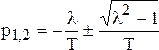(4.23)

могут быть вещественными, комплексными или чисто мнимыми, определяя в каждом случае свой переходный процесс. При этом обычно говорят о трех типах звеньев.

Апериодическое звено второго порядка

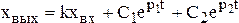. (4.24)

Переходный процесс имеет апериодический характер, протекающий без колебаний (рис. 4.6,а).

Можно показать, что в этом режиме звено эквивалентно последовательному соединению двух апериодических звеньев первого порядка с постоянными времени T ₁ , T₂ и коэффициентами передачи k₁ , k₂ . Поэтому передаточная функция звена может быть записана также в виде

.

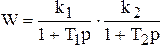Колебательное звено

,

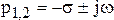где 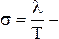коэффициент затухания, а 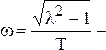угловая частота свободных колебаний. Переходная характеристика колебательного звена определяется уравнением

,

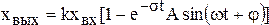где 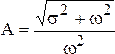и 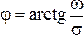— соответственно амплитуда, и фаза свободных колебаний. Переходный процесс показан на рис. 4.6,б.

Консервативное звено

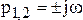, (4.27)

и звено представляет собой идеализированный случай звена без потерь. Переходный процесс носит незатухающий колебательный характер (рис.4.6, в).

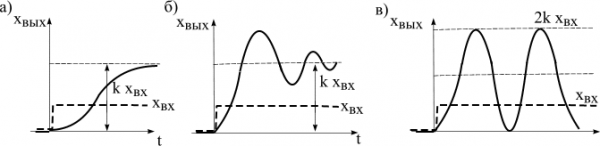Рис. 4.6. Переходные функции инерционных звеньев второго порядка

Примеры. К инерционным звеньям второго порядка относятся элементы, способные запасать потенциальную и кинетическую энергию и преобразовывать их одну в другую. Такими возможностями обладают: электрические R-L-С контуры; электромеханические устройства, например, двигатели, у которых кинетическая энергия запасается в якоре, а электромагнитная (потенциальная) в якорной цепи; механические элементы, обладающие массой, упругостью и вязким трением и т. д.

Пример 4.2.

.

Используя известные формулы: 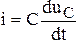, , 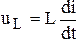, 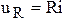получим

.

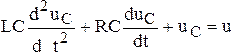Это уравнение инерционного звена второго порядка, в котором , .

Все темы данного раздела:

Любую автоматическую систему можно условно разделить на две части – объект управления и управляющее устройство. Взаимодействие этих частей между собой схематично показано на рис.1.1.

Для любого физического объекта может быть составлена математическая модель, которая представляет собой набор определенных математических соотношений между переменными величинами это

Несмотря на большое разнообразие технических процессов и объектов, в которых используется автоматическое управление, организация управления основывается на небольшом числе общих принципов это:

В исследовании динамики автоматических систем широко применяются интегральные преобразования Лапласа, Хевисайда-Карсона, Фурье. Одна из привлекательных сторон этих преобразований в том, что они пон

Под статической характеристикой физического объекта понимают уравнение вида (3.1)

По виду статических характеристик все автоматические системы делятся на статические и астатические, или говорят о статическом и астатическом регулировании. Пр

1. Объект регулирования (рис.3.2).

Объектом регулирования является генератор постоянного т

1. Объект регулирования.Объектом регулирования является двигатель постоянного тока независимого возбуждения, для которого справедливы следующие уравнения

Автоматические системы состоят из разнообразных элементов, среди которых могут быть генераторы, двигатели, термопары, реостаты, редукторы и многие другие конструкции. Но при математ

Автоматические системы относятся к классу динамических систем, потому что процессы регулирования, протекающие в них, сопровождаются постоянными изменениями во времени. Математическое описание этих

Понятием типовое звено в теорию введен еще один исключительно удобный расчетно-аналитический инструмент. Из всего многообразия возможных динамических звеньев выделена группа

Уравнение динамики этого звена описывается алгебраическим уравнением

Уравнение динамики звена , (4.16) где Т –

Интегрирующим называется звено, в котором производится интегрирование входного воздействия, и поэтому в выходном воздействии обязательно присутствует интеграл

Дифференцирующие звенья реагируют на скорость изменения входного воздействия, и поэтому в их дифференциальных уравнениях в правой части содержатся производные от входной переменной.

Запаздывающим называется звено в котором выходное воздействие повторяет входное воздействие без искажений, но с некоторым постоянным запаздыванием во времени на величину t. Эти условия определяют у

Апериодическое звено. АФХ этого звена определяется выражением

Покажем технику построения ЛЧХ на примере двух динамических звеньев. Безынерционное звено. Логарифмируя частотную передаточную функцию (4.15) , найдем

Под начальными условиями дина­мического процесса понимается его со­стояние в момент времени, принятый за начало процесса. Начальные усло­вия задаются совокупностью значений выходной координаты иссл

Под устойчивостью понимают способность системы самостоятельно приходить к установившемуся состоянию после приложения воздействия, которое вывело ее из состояния равновесия.

Свободное движение линейной системы описывается однородным дифференциальным уравнением . (6.1)

Для того, чтобы система была устойчивой, должны выполняться определенные условия, которые называются условиями устойчивости. Все условия устойчивости разделяются на необходимые и достаточные

Все критерии устойчивости делятся на алгебраические и частотные. Если для работы с алгебраическими критериями необходимо иметь, по крайней мере, характеристическое ура

Запас устойчивости – это количественная оценка, определяющая удаление расчетных параметров системы от зоны, опасной с точки зрения устойчивости. Формулировка запаса

Рассмотренные выше вопросы устойчивости, строго говоря, справедливы только для линейных систем. Но почти все реальные системы являются нелинейными, и поэтому возникает вопрос — наск

Из предыдущей главы мы знаем, что автоматическая система, прежде всего, должна быть устойчивой. В устойчивой системе переходный процесс затухает, однако для практики вовсе не безразлично то, как эт

Метод распределения корней.Этот метод дает возможность приближенно оценить характер переходного процесса по расположению корней относительно мнимой оси. В основу ме

Процесс проектирования автоматической системы можно условно разбить на два этапа. На первом этапе закладывается функциональная схема системы, выбираются ее элементы, задаются законы

Предположим, что в системе появилось рассогласование, то есть действительное значение регулируемой величины стало отличаться от заданного значения. Как должна реагировать система на эту ситуацию? Р

Понятие о коррекции. В автоматических системах, которые состоят только из основных функционально необходимых элементов, обычно не удается получить требуемые показат

Расчет системы автоматического регулирования (САР) представляет собой задачу, имеющую, как правило, многозначное решение. Выбор оптимальной кон­фигурации САР зависит от требований, предъявляемых ка

Выбор параметров объекта управления. Так как в техническом задании уже определен тип исполнительного двигателя, то остается только выбрать его каталожные данные и согласовать их с техническими данн

Статическая модель описывает систему в установившемся режиме и по­этому используется для расчета параметров настройки ее элементов, при ко­торых будут обеспечены заданные в ТЗ параметры статических

В уравнениях динамической модели присутствует координата времени, и поэтому модель представляет собой систему дифференциально-алгебраичес­ких уравнений. Примечание. Так как решен

9.3.3.1. Динамические характеристики САР. Динамической характерис­тикой САР является функциональная зависимость между переменными моде­ли. Последовательность получения х

В методических указаниях показаны основные принципы начального эта­па разработки автоматической системы. Это первичная компоновка схемы, оп­ределение параметров настройки и расчеты статических и ди

1. В.А.. Бесекерский, Теория систем автоматического регулиро­вания. В. А. Бесекерский, Е. П. Попов. – М. : Наука, 1975. — 457 с. 2.Куропаткин, П.В. Теория автоматического управления./ П.В.