Основное направление исследования клеточных автоматов — алгоритмическая разрешимость тех или иных проблем. Также рассматриваются вопросы построения начальных состояний, при которых клеточный автомат будет решать заданную задачу.
1. История
Станислав Улам, работая в Лос-аламосской национальной лаборатории в 1940-е годы, изучал рост кристаллов, используя простую решёточную модель. В это же время Джон фон Нейман, коллега Улама, работал над проблемой самовоспроизводящихся систем. Первоначальная концепция фон Неймана основывалась на идее робота, собирающего другого робота. Такая модель известна как кинематическая. Разработав эту модель, фон Нейман осознал сложность создания самовоспроизводящегося робота и, в частности, обеспечения необходимого «запаса частей», из которого должен строиться робот. Улам предложил фон Нейману использовать более абстрактную математическую модель, подобную той, что Улам использовал для изучения роста кристаллов. Таким образом возникла первая клеточно-автоматная система. Подобно решётке Улама, клеточный автомат фон Неймана двухмерный, а самовоспроизводящийся робот описан алгоритмически. Результатом явился универсальный конструктор, работающий «внутри» клеточного автомата с окрестностью, включающей непосредственно прилегающие ячейки, и имеющего 29 состояний. Фон Нейман доказал, что для такой модели существует паттерн, который будет бесконечно копировать самого себя.
Также в 1940-е годы, Норберт Винер и Артуро Розенблют разработали клеточно-автоматную модель возбудимой среды. Целью было математическое описание распространение импульса в сердечных нервных узлах. Их оригинальная работа продолжает цитироваться в современных исследованиях по аритмии и возбудимым средам.
В 1960-е годы клеточные автоматы изучались как частный тип динамических систем, и впервые была установлена их связь с областью символьной динамики. В 1969 году Г.А.Хедланд провёл обзор результатов, полученных в этом направлении. Наиболее значимым результатом явилось описание набора правил клеточного автомата как множества непрерывных эндоморфизмов в сдвиговом пространстве.
В 1970-е получила известность двухмерная клеточно-автоматная модель с двумя состояниями, известная как игра «Жизнь». Изобретенная Джоном Конвеем и популяризованная Мартином Гарднером, она использует следующие правила: если клетка имеет двух «живых» соседей, она остаётся в прежнем состоянии. Если клетка имеет трёх «живых» соседей, она переходит в «живое» состояние. В остальных случаях клетка «умирает». Несмотря на свою простоту, система проявляет огромное разнообразие поведения, колеблясь между очевидным хаосом и порядком. Одним из феноменов игры «Жизнь» являются глайдеры — сочетания клеток, движущиеся по сетке как единое целое. Возможно построить автомат, в котором глайдеры будут выполнять некоторые вычисления, и впоследствии было показано, что игра «Жизнь» может эмулировать универсальную машину Тьюринга.
Основные виды межотраслевых моделей прогнозирования (2)
... балансовой межотраслевой модели и её особенности исследовать модель динамического межотраслевого баланса и модель В.В. Леонтьева «затраты - выпуск» Объектом работы является прогнозирование. Предметом - межотраслевые модели ... субъекта. Существует три основных типа прогноза: прогноз развития технологий, экономики и продаж ... применено Пьером Ваком в 1971 году. Прогнозирование сценария сложилось в ...
В 1969 году немецкий инженер Конрад Цузе опубликовал книгу «Вычислимый космос», где выдвинул предположение, что физические законы дискретны по своей природе, и что вся Вселенная является гигантским клеточным автоматом. Это была первая книга из области, называемой сейчас цифровой физикой.
В 1983 Стивен Вольфрам опубликовал первую из серии статей, исследующих очень простой, но до сих пор неизученный класс клеточных автоматов, называемых элементарными клеточными автоматами. Неожиданная сложность поведения этих простых автоматов привела Вольфрама к предположению, что сложность естественных систем обусловлена сходным механизмом. Кроме того, в течение этого периода Вольфрам формулирует концепцию истинной случайности и вычислительной неприводимости, и выдвигает предположение, что правило 110 ( англ. ) может быть универсальным — факт, доказанный в 1990 году ассистентом Вольфрама Мэтью Куком.
В 2002 году Вольфрам публикует 1280-страничный текст «Новый тип науки» (A New Kind of Science), где широко аргументирует, что достижения в области клеточных автоматов не являются изолированными, но весьма устойчивы и имеют большое значение для всех областей науки.
11-го ноября 2002 года Пауль Чепмен (Paul Chapman) построил образец Жизни, который является РММ (Регистровой Машиной Минского).
Фактически РММ эквивалентна машине Тьюринга. Первая версия образца была большой (268,096 живых ячеек на площади 4,558 x 21,469 клеток) и медленной (20 поколений/сек при использовании Life32 Иогана Бонтеса (Johan Bontes) на 400 MHz AMD K6-II).
Таким образом, в игре Жизнь можно выполнить любой алгоритм, который можно реализовать на современном компьютере.
2. Математическое определение
Клеточный автомат можно определить как множество конечных автоматов, каждый из которых может находиться в одном из состояний
-
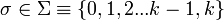 .
.
Изменение состояний автоматов происходит согласно правилу перехода
-
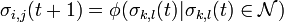 ,
,
где 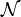 — множество автоматов, составляющих соседство. К примеру, соседство фон Неймана определяется как
— множество автоматов, составляющих соседство. К примеру, соседство фон Неймана определяется как
-
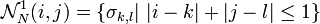 ,
,
а соседство Мура
Автомат Калашникова — история и современность
... на вооружение Советской армии в двух вариантах под обозначениями "7.62мм автомат Калашникова АК" и "7.62мм автомат Калашникова со складным прикладом АКС" (для воздушно-десантных войск). Серийное ... испытаний в 1959 году на вооружение Советской армии был принят "7.62мм автомат Калашникова модернизированный АКМ", как продемонстрировавший высокую надежность, приемлемые характеристики по точности и ...
-
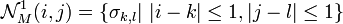 .
.
Число всех возможных правил перехода определяется числом состояний σ и количеством соседей n и составляет
-
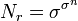 [1]
[1]
3. Свойство обратимости
обратимым
Для одномерных клеточных автоматов существуют алгоритмы определения обратимости или необратимости. Однако для клеточных автоматов с двумя и более измерениями таких алгоритмов нет.
Обратимые клеточные автоматы часто используют для моделирования таких физических феноменов, как динамика жидкости и газа, поскольку они подчиняются законам термодинамики. Такие автоматы специально создаются обратимыми. Такие системы изучались Томасо Тоффоли (Tommaso Toffoli) и Норманом Марголусом (Norman Margolus).
Существует несколько типов обратимых конечных автоматов. Наиболее известными являются клеточный автомат второго порядка и блочный клеточный автомат. Обе эти модели следуют несколько модифицированному варианту определения клеточного автомата, однако доказано, что они могут быть эмулированы традиционным клеточным автоматом со значительно большим размером соседства и числом состояний. Также, было доказано, что любой обратимый клеточный автомат может быть сэмулирован блочным клеточным автоматом.
4. Клеточные автоматы в естественной среде
Некоторые живые организмы проявляют свойства клеточных автоматов. Раскраска некоторых морских ракушек, таких как Conus или Cymbiola, генерируется естественным клеточным автоматом. Их пигментные клетки располагаются тонкой полоской вдоль края раковины. Секреция пигмента каждой клетки зависит от активирующей и ингибиторной активности соседних клеток. В процессе роста полоса клеток оставляет цветной паттерн на поверхности ракушки.
Растения регулируют приток и отток газообразных веществ посредством механизма клеточных автоматов. Каждое устьице на поверхности листа действует как ячейка.
Нейронные сети также могут быть использованы как клеточные автоматы. Сложный движущийся узор на коже головоногих является отражением паттернов активирования в мозгу животных.
Реакция Белоусова-Жаботинского представляет собой пространственно-временной химический осциллятор, который может быть смоделирован клеточным автоматом. В 1950-х годах А.М.Жаботинский, продолжая работу Б.П.Белоусова, обнаружил, что тонкий однородный слой смеси определённых химических веществ способен образовывать движущиеся геометрические узоры, такие как концентрические круги и спирали.
Примечания
Данный реферат составлен на основе .
