Учение о свойствах вещества в различных агрегатных состояниях основывается на представлениях об атомно-молекулярном строении материального мира. В основе молекулярно-кинетической теории строения вещества (МКТ) лежат три основных положения:
- все вещества состоят из мельчайших частиц (молекул, атомов, элементарных частиц), между которыми есть промежутки;
- частицы находятся в непрерывном тепловом движении;
- между частицами вещества существуют силы взаимодействия (притяжения и отталкивания); природа этих сил электромагнитная.
Значит, агрегатное состояние вещества зависит от взаимного расположения молекул, расстояния между ними, сил взаимодействия между ними и характера их движения.
Сильнее всего проявляется взаимодействие частиц вещества в твердом состоянии. Расстояние между молекулами примерно равно их собственным размерам. Это приводит к достаточно сильному взаимодействию, что практически лишает частицы возможности двигаться: они колеблются около некоторого положения равновесия. Они сохраняют форму и объем.
Свойства жидкостей также объясняются их строением. Частицы вещества в жидкостях взаимодействуют менее интенсивно, чем в твердых телах, и поэтому могут скачками менять свое местоположение – жидкости не сохраняют свою форму – они текучи. Жидкости сохраняют объем.
Газ представляет собой собрание молекул, беспорядочно движущихся по всем направлениям независимо друг от друга. Газы не имеют собственной формы, занимают весь предоставляемый им объем и легко сжимаются.
Существует еще одно состояние вещества – плазма. Плазма — частично или полностью ионизованный газ, в котором плотности положительных и отрицательных зарядов практически одинаковы. При достаточно сильном нагревании любое вещество испаряется, превращаясь в газ. Если увеличивать температуру и дальше, резко усилится процесс термической ионизации, т. е. молекулы газа начнут распадаться на составляющие их атомы, которые затем превращаются в ионы.
Модель идеального газа. Связь между давлением и средней кинетической энергией.
Для выяснения закономерностей, которым подчиняется поведение вещества в газообразном состоянии, рассматривается идеализированная модель реальных газов – идеальный газ. Это такой газ, молекулы которого рассматриваются как материальные точки, не взаимодействующие друг с другом на расстоянии, но взаимодействующие друг с другом и со стенками сосуда при столкновениях.
Называется состояние веществ
... и давление. Жидкость есть агрегатное состояние вещества, сочетающее в себе черты твердого состояния (сохранение объема, определенная прочность на разрыв) и газообразного (изменчивость формы). Для жидкости характерны ближний порядок в расположении частиц (молекул, атомов) ...
Идеальный газ
Идеальный газ – это модель, придуманная учеными для познания газов, которые мы наблюдаем в природе реально. Она может описывать не любой газ. Не применима, когда газ сильно сжат, когда газ переходит в жидкое состояние. Реальные газы ведут себя как идеальный, когда среднее расстояние между молекулами во много раз больше их размеров, т.е. при достаточно больших разрежениях.
Свойства идеального газа:
- расстояние между молекулами много больше размеров молекул;
- молекулы газа очень малы и представляют собой упругие шары;
- силы притяжения стремятся к нулю;
- взаимодействия между молекулами газа происходят только при соударениях, а соударения считаются абсолютно упругими;
- молекулы этого газа двигаются беспорядочно;
- движение молекул по законам Ньютона.
параметрами состояния.
Объем газа
Давление – физическая величина, равная отношению силы F, действующей на элемент поверхности перпендикулярно к ней, к площади S этого элемента .
p = F/S Единица давления в СИ паскаль [Па]
До настоящего времени употребляются внесистемные единицы давления:
техническая атмосфера
физическая атмосфера
миллиметры ртутного столба
1 атм = = 760 мм рт. ст. = 1013 гПа.
Как возникает давление газа? Каждая молекула газа, ударяясь о стенку сосуда, в котором она находится, в течение малого промежутка времени действует на стенку с определенной силой. В результате беспорядочных ударов о стенку сила со стороны всех молекул на единицу площади стенки быстро меняется со временем относительно некоторой (средней) величины.
Давление газа
давление газа на стенку сосуда
x
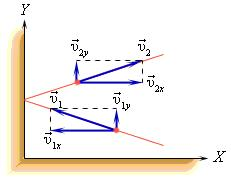
манометрами.
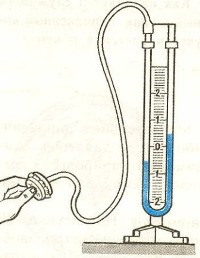
Жидкостные манометры:
- открытый – для измерения небольших давлений выше атмосферного
- закрытый — для измерения небольших давлений ниже атмосферного, т.е. небольшого вакуума

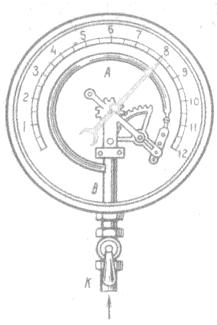
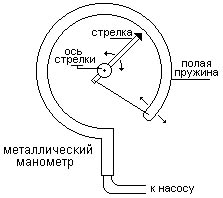
Металлический манометр

Основной его частью является изогнутая трубка А, открытый конец которой припаян к трубке В, через которую поступает газ, а закрытый – соединен со стрелкой. Газ поступает через кран и трубку В в трубку А и разгибает её. Свободный конец трубки, перемещаясь, приводит в движение передающий механизм и стрелку. Шкала градуирована в единицах давления.
Основное уравнение молекулярно-кинетической теории идеального газа., Основное уравнение МКТ
p = 1/3·m 0· n·v2
Механика жидкостей и газов в законах и уравнениях
... давления вдоль трубки -- в местах, где скорость больше, давление должно быть меньше, и наоборот. Аналитическую связь между скоростью течения и давлением мы уста-новим в следующем параграфе. 2. Уравнение Бернулли В реальных жидкостях ... заключенной в рассматри-ваемом объеме жидкости. Силы давления на стенки трубки тока перпенди-кулярны в каждой точке к направлению перемещения жидкости, вследствие чего ...
m 0 — масса одной молекулы газа;
- n = N/V – число молекул в единице объема, или концентрация молекул;
v 2 — средняя квадратичная скорость движения молекул.
Так как средняя кинетическая энергия поступательного движения молекул E = m 0 *v2 /2, то домножив основное уравнение МКТ на 2, получим p = 2/3· n·(m0 · v2 )/2 = 2/3·E·n
p = 2/3·E·n
Давление газа равно 2/3 от средней кинетической энергии поступательного движения молекул, которые содержатся в единичном объеме газа.
p = 1/3· ρ· v 2
Объединенный газовый закон.
термодинамическими параметрами газа.
объем V, давление р и температура Т.
термодинамическим процессом.
В любом термодинамическом процессе изменяются параметры газа, определяющие его состояние.
газовым законом
объединенным газовым законом.
p = nkT
p = nkT
![]()
где n – концентрация молекул, N – общее число молекул, V – объем газа
Тогда получим ![]() или
или ![]()
Так как при постоянной массе газа N остается неизменным, то Nk – постоянное число, значит
![]()
При постоянной массе газа произведение объема на давление, деленное на абсолютную температуру газа, есть величина одинаковая для всех состояний этой массы газа.
уравнением Клайперона
Уравнение Клайперона можно записать в другой форме.
p = nkT,
учитывая, что
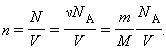
Здесь N – число молекул в сосуде, ν – количество вещества, N А – постоянная Авогадро, m – масса газа в сосуде, M – молярная масса газа. В итоге получим:
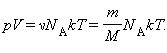
универсальной (молярной) газовой постоянной
R = 8,31 Дж/моль·К
Соотношение
![]()
уравнением состояния идеального газа
уравнением Клапейрона–Менделеева.`
Понятие реального газа
... постоянная Ван-дер-Ваальса, характеризующая силы межмолекулярного притяжения, Vm - молярный объём. Вводя эти поправки - получим уравнение Ван-дер-Ваальса для моля газа (уравнение состояния идеальных газов): ... 0,003663 град-1. 1. Понятие реального газа Реальный газ При рассмотрении реальных газов - газов, свойства которых зависят от взаимодействия молекул, надо учитывать силы межмолекулярного ...
Для одного моля любого газа это соотношение принимает вид: pV=RT
физический смысл молярной газовой постоянной
Запишем уравнение pV=RT для нагретого газа: p ( V + ΔV ) = R (T + 1)
и вычтем из этого равенства уравнение pV=RT , соответствующее состоянию газа до нагревания. Получим pΔV = R
ΔV = SΔh, где S – площадь основания цилиндра. Подставим в полученное уравнение:
pSΔh = R
pS = F – сила давления.
Получим FΔh = R, а произведение силы на перемещение поршня FΔh = А – работа по перемещению поршня, совершаемая этой силой против внешних сил при расширении газа.
Таким образом, R = A .
Универсальная (молярная) газовая постоянная численно равна работе, которую совершает 1 моль газа при изобарном нагревании его на 1 К.
