Рабочая площадка промышленного здания

метки: Рабочий, Промышленный, Здание, Площадка, Прочность, Устойчивость, Металл, Требовать

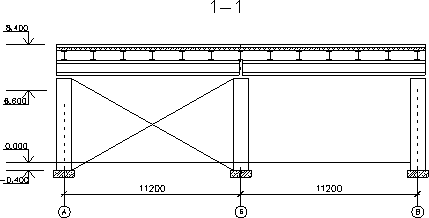
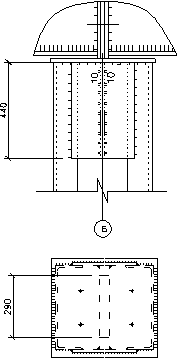
Разрез 1 — 1

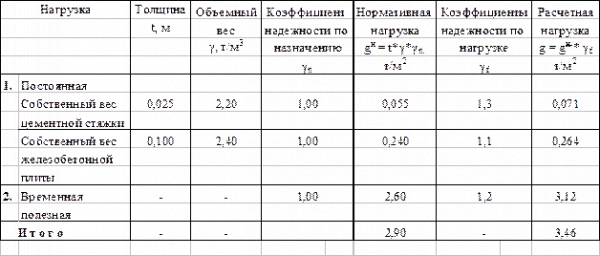
3. Сбор нагрузок на 1 м² настила

Таблица 1

Нагрузка на 1 м ² настила

4. Расчет балки настила Б1

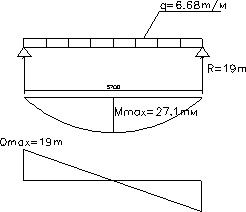
4.1 Расчетная схема

4.2 Сбор нагрузок

Нагрузка на 1 погонный метр балки:

1. Нормативная:

Нагрузка от собственного веса 1 погонного метра балки q _с.в = 0,100 т/м.

q ^н = g^н * a + q_с.в = 2,60*1,9+0,100 = 5,61 т/м

2. Расчетная:

Коэффициент надежности по нагрузке γ _f = 1,05.

q = g* a + q _с.в * γ_f = 3,46*1,9+0,100*1,05 = 6,68 т/м

4.3 Статический расчет

Максимальный расчетный изгибающий момент (в середине пролета)

М _max = q * l² / 8 =6,68 *5,7² / 8 = 27,13 т*м

Максимальный нормативный изгибающий момент

М ^н _max = М_max * q^н / q = 27,13*5,61/6,68 = 30,0 т*м

Максимальная расчетная поперечная сила (на опоре)

Q _max = R = q * l / 2 = 6,68*5,7/2 = 19,04 т

4.4 Выбор материала

По таблице 50* СниП II – 23 – 81* для балок перекрытий, работающих при статических нагрузках, при отсутствии сварных соединений в условиях климатического района II ₅ выбираем сталь марки С245 (ГОСТ 27772 — 88).

Толщина полки двутавра ориентировочно t _f = 2– 20 мм.

По таблице 51* СниП II – 23 – 81* для стали марки С245 при t _f = 2 – 20 мм расчетное сопротивление по пределу текучести R_y = 2450 кг/см² .

4.5 Подбор сечения

Требуемый момент сопротивления

W _x ^тр = M_max / (R_y *γ_c *c₁ )

Коэффициент условий работы (таблица 6* СНиП II – 23 – 81*) γ _c = 1,0.

Балки и балочные конструкции

... балок 3. Настилы балочных клеток В качестве несущего настила чаще всего применяют плоские стальные листы или настил из сборных железобетонных плит. Полезная нагрузка на настил перекрытий ... момент. При расчете принимается опирание настила шарнирно неподвижным. Рис. 5. Расчетная схема настила, эпюра моментов, конструкция крепления настила к балке При нагрузке ... 7 СНиП. При этом за расчетную длину балки l ...

Коэффициент, учитывающий развитие пластических деформаций, с ₁ = с (так как в месте действия M_max и в непосредственной близости от него т < 0,5*R_s ).

Отношение площадей сечений полки и стенки ориентировочно A _f / A_w = 0,75 => с₁ = с = 1,095 (таблица 66 СНиП II – 23 – 81*).

W _x ^тр = 27,1*10⁵ / (2450*1,0*1,095) = 1011,3 см³

Из условия W _x ≥ W_x ^тр = 1011 см³ принимаем двутавр  40Б3 с параллельными гранями полок по ТУ 14–2–24-72 с моментом сопротивления W_x = 1020 см³ >W_x ^тр = 1011 см³ .

4.6 Геометрические характеристики сечения

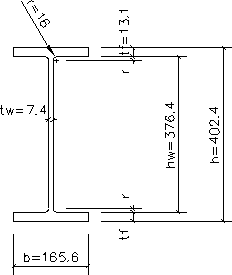h = 402,4 мм;

• b = 165,6 мм;

t _w = 7,4 мм;

t _f = 13,1 мм;

• r = 16 мм;

A = 73,4 см ² ;

• Масса 1 м длины = 57,6 кг;

I _x = 20480 см⁴ ;

W _x = 1020 см.

Высота стенки h _w = h – 2*t_f = 402,4-2*13,1 = 376,4 мм;

Расчетная высота стенки h _{е f} = h_w – 2*r = 376,4-2*16 = 344,4 мм.

Условная гибкость

Λ _w = Λ_w * √ R_y / E

Λ _w = h_{е f} / t_w = 344,4/7,4 = 46,54

Λ _w = 46,54*√ 2450 / (2,1*10⁶ ) = 1,59 < 2,2

A _f = t_f * b = 1,31*165,6 = 21,7 см²

A _w = h_w * t_w = 37,64*0,74 = 27,85 см²

A _f / A_w =21,7 / 27,85 = 0,78

4.7 Проверка принятого сечения

1. По прочности (I группа предельных состояний)

Условное нормальное напряжение при упругой работе балки (в пролете) W _ey = c₁ * W_x

c ₁ = c = 1 + (1 – ξ² ) / (2 + 12* A_f / A_w ) = 1+(1-0,2² )/(2+12*0,78) = 1,085

Минимальная относительная высота упругой зоны, соответствующая максимальной остаточной деформации, допускаемой нормами СНиП II – 23 – 81* ξ = 2*d / h = 0,2.

σ = M _max / (c₁ * W_x ) = 27,1*10⁵ / (1,085*1020) = 2448 кг/см² <R_y * γ_c = 2450 кг/см² → прочность обеспечена.

Недонапряжение (2450-2448) / 2450 *100% = 0,08%.

а) Разница между весом 1 м балки (57,6 кг) и его значением, принятым предварительно, составляет 0,87% от полной нагрузки q на балку ((100-57,6) /4850 *100% = 0,87%), поэтому уточнения величины q не производим.

б) Так как недонапряжение составляет 0,1%< 5%, значит проверка двутавра с меньшей площадью не требуется.

Технология сварочных работ по производству подкрановой балки

... работ на поперечный изгиб. Типы поперечных сечений и размеры сварных балок весьма разнообразны. Если нагрузка приложена в вертикальной плоскости, то чаще всего используют балки двутаврового сечения. Сварочные двутавровые балки ...

Таким образом, окончательно принимаем двутавр  45Б3 по ТУ 14–2–24-72.

в) Так как недонапряжение 0.1% < (с₁ – 1)*100% = (1,09-1)*100% = 9%, то балка работает в упругопластической стадии.

Относительная высота упругого ядра ξ _Ф < 1

Максимальное нормальное напряжение (в середине пролета)

Касательное напряжение на опоре при этажном сопряжении

т = Q _max / A_w = 19.04*10³ / 27.85 = 684 кг/см² < R_s * γ_c = 0,58 * R_y * γ_c = 0,58*2450 = 1420 кг/см²

Касательное напряжение при сопряжении в одном уровне

т = Q _max / (0,8*A_w ) = 19*10³ / (0,8*27.85) = 855 кг/см² < R_s * γ_c = 1420 кг/см²

Коэффициент, учитывающий ослабление болтами при сопряжении балок в одном уровне, 0,8.

2. Местная устойчивость

Так как Λ _w = 1,59 < 2,2, местную устойчивость проверять не будем.

3. Общая устойчивость (I группа предельных состояний)

Обеспечена настилом, так как имеются соответствующие конструктивные элементы, связывающие настил с балкой.

4. По деформативности при нормальных условиях эксплуатации (II группа предельных состояний)

[ f / l ] = 1/250 (по таблице 40 СНиП II – 23 – 81*).

f / l = M ^н _max * l / (10 * E * I_x ) = 22.8*10⁵ *570 / (10*2,1*10⁶ *20480) = 1/331 < [ f / l ] = 1/250

5. Расчет главной балки Б2

5.1 Расчетная схема

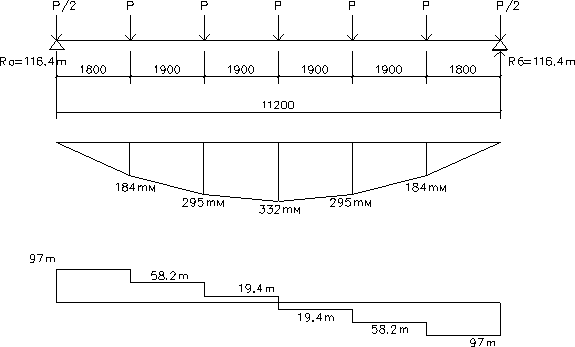
5.2 Сбор нагрузок

Р = Р’ * 1,02 = q * l *1,02 = 6.68*5.7*1,02 = 38.8 т

Где коэффициент 1,02 учитывает собственный вес балки.

5.3 Статический расчет

При симметричной нагрузке:

R _A = R_B = ∑P / 2 = 6*P / 2 = 6*38.8/2 =116.4 т

М _x=а = (R_A – 0,5*Р) * а’ = (116,4-0,5*38,8)*1,8 = 184 т*м

М _x=2*а = (R_A – 0,5*Р) * (a’+ а) – Р*а = (116,4-0,5*38,8)*(1.8+1,9)-38,8*1,9 = 295 т*м

М _x=3*а = (R_A – 0,5*Р) * (a’+2 * а) – Р*2*а — Р*а = (116,4-0,5*38,8)*(1.8+2*1,9)-38,8*2*1,9-38,8*1,9 = 332 т*м

Q _max = R_A – 0,5*Р = 116,4 – 0,5*38,8 = 97 т

Проверка величины М _max :

При распределенной нагрузке q _Б2 = g * (l₁ + l₂ ) / 2*1,04 = (3,46*(5,7+5,7) / 2)*1,04 = 20,5т/м

Коэффициент, учитывающий собственный вес балки 1,04.

М _max ‘ = q_Б2 * L₁ ² / 8 = 20,8*11,2² / 8 = 331 т*м = М_max = 332 т*м

5.4 Выбор материала

По таблице 50* СниП II – 23 – 81* для балок перекрытий, работающих при статических нагрузках, при отсутствии сварных соединений в условиях климатического района II ₅ выбираем сталь марки С235 (ГОСТ 27772 — 88).

Толщина полки двутавра ориентировочно t _f = 2 – 20 мм.

По таблице 51* СниП II – 23 – 81* для стали марки С235 при t _f = 2 – 20 мм расчетное сопротивление материала пояса по пределу текучести R_y = 2350 кг/см² .

Клеефанерная балка деревянные конструкции

... (или 3) сорта. Расчет ребристых клеефанерных балок производят на изгиб с учетом совместной работы дощатых поясов и фанерных стенок. В двускатных балках переменной высоты сечения, где при равномерной нагрузке действуют максимальные ...

5.5 Подбор основного сечения

Расчет ведем без учета пластических деформаций.

1. Требуемый момент сопротивления сечения

W _x ^тр = M_max / (R_y *γ_c ) = 332*10⁵ /(2350*1,0) = 13830 см³

2. Условная гибкость

Λ _w = Λ_w * √ R_y / E

Гибкость стенки примем Λ _w = h_{е f} / t_w = h_w / t_w = 130

Λ _w = 130*√ 2350 / (2,1*10⁶ ) = 4,35

3. Оптимальная высота балки

h _опт ‘ = ³ √ 1,5 * W_x ^тр * Λ_w = ³ √ 1,5*13830*130 = 139,2 cм

Для балки переменного сечения оптимальная высота

h _опт ≈ 0,95 * h_опт ‘ = 0,95*139,2 = 132,2 см

Минимальная высота балки

h _min = L₁ * R_y / (10⁷ * [f / l]) * q^н / q = 11200*2350 / (10^{7 *} 1/400)*5,61 /6,68 = 88,4 см

[ f / l ] = 1/400 (по таблице 40 СНиП II – 23 – 81*).

Максимальная строительная высота перекрытия

h _{стр, mах} = d_н – d_{б, min} = 8,4-6,6 = 1,8 м

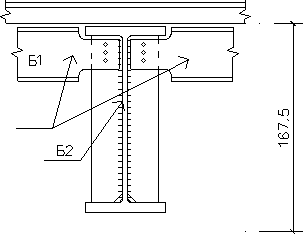
Максимальная высота при этажном сопряжении главных балок и балок настила

h _{m ах} ^этажн = h_{стр, mах} – (t_ст + t_пл + h_Б1 ) = 180-(2,5+10+40,3) = 127,2 см

h _{m ах} ^{одн ур} = h_{m ах} ^этажн + h_б1 = 127,2 +40,3 = 167,5см

Так как h _{m ах} ^этажн = 127,2 см < h_опт = 132,2 см, то этажное сопряжение не подходит.

Принимаем h _б = h_опт = 132,2 см

Условие h _min = 88,4 см < h_б = 132,2 см < h_{m ах} ^одн.ур = 167,5 см выполнено.

Высота стенки h _w ≈ 0,98 * h_б = 0,98*132,2 = 130 см

4. Толщина стенки с учетом принятой гибкости

t _w = h_w / Λ_w = 130/130 = 1 cм

По условиям коррозионной стойкости t _w =1 cм > t_w = 0,6 см → условие выполнено.

По условию прочности в опорном сечении при работе на сдвиг

t _w =1 cм > t_w = 3/2 * Q_max / (h_w *R_s ) = 3/2*97*10³ / (130*1360) = 0,82 см → условие выполнено.

R _s = 0,58 * R_y = 0,58*2350 = 1360 кг/см²

Так как h _w = 1300 мм >1050 мм, то принимаем стенку из толстолистовой стали толщиной t_w =10 мм.

Площадь сечения стенки

A _w = h_w * t_w = 130*1 = 130 см²

5. Требуемая площадь пояса

A _f ^тр = W_x ^тр / h_w — h_w * t_w / 6 = 13830/130 – 130*1/6 = 84,7 см²

Анализ условий работы первичного газового холодильника

... первичном газовом холодильнике основной процесс – охлаждение коксового газа до заданной температуры, здесь наблюдается процесс теплопроводности. Уравнение теплопроводности для установившегося теплового потока через цилиндрическую однослойную стенку ... Это приводит к ухудшению условий теплопередачи – нарушению ... сечение [2], к двум вертикальным стенкам которого развальцовкой закреплены трубы 3. Стенки ...

Проверка сечения:

A _{f , min} ^тр = 0,5 *( A_min ^тр — A_w ) = 0,5*(298,1-130) = 84,5 см²

A _min ^тр = 3 * W_x ^тр / h_опт ‘ = 3*15932/145,9 = 327,6 см²

По ГОСТ 82 – 70* принимаем сечение с размерами: t _f = 20 мм;

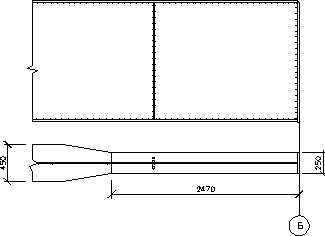
Требования:

а) h_w / 5 ≤ b_f ≤ h_w / 2,5

1300/5 ≤ b _f ≤ 1300/2,5

260 мм ≤ b _f = 450 мм ≤ 520 мм → условие выполнено.

б) При изменении сечения по ширине

b _f ≥ 300 мм

b _f = 450 мм ≥ 300 мм → условие выполнено.

При изменении сечения по толщине

b _f ≥ 180 мм

b _f = 450 мм ≥ 180 мм → условие выполнено.

в) При изменении сечения по ширине

b _f ≤ 30 * √ 2100 / R_y * t_f

b _f = 450 мм ≤ 30 * √ 2100 / 2350 * 20 = 567 мм → условие выполнено.

г) t_f ≤ 3 * t_w

t _f = 20 мм ≤ 3 * 10 = 30 мм → условие выполнено.

д) t_f = 20 мм → условие выполнено.

Окончательные размеры основного сечения:

стенка A_w = h_w * t_w = 130*1 = 130 см² ;

пояс A_f = t_f * b_f = 2,0 * 45 = 90,0 см² > A_f ^тр = 84,7 см²

6. Геометрические характеристики основного сечения

h _б = h_w + 2 * t_f = 130+2*2,0 = 134 см;

A _f = 90 см² ;

A _w = 130 см² ;

А = 2 * A _f + A_w = 2*96+148,5 = 310 см² ;

A _f / A_w = 90 / 130 = 0,692;

Λ _w = h_w / t_w * √ R_y / E = 130 / 1*√2350 / (2,1*10⁶ ) = 4,35

Момент инерции стенки

I _w = t_w * h_w ³ / 12 = 1*130³ / 12 =183 *10³ см⁴ ;

Момент инерции поясов

2 * I _f = 2*A_f * z² = 2*90*66² = 784*10³ см⁴ ;

z = 0,5 * h _w + 0,5 * t_f = 0,5*130+0,5*2,0 = 66 см

Момент инерции основного сечения

I _х = I_w + 2 * I_f = 183*10³ +784*10³ = 967 * 10³ см⁴ ;

Момент сопротивления сечения

W _x = I_x / (0,5 * h_б ) = 967*10³ / (0,5*134) = 14430 см³ > W_x ^тр = 13830 см³ .

Разработка стенда по проверке, испытанию и диагностике генераторов ...

... размеры - 565х750х525 мм. Стенд для диагностики генераторов и стартеров MD1 На рисунке 1.4 представлен стенд для диагностики генераторов и стартеров MD1. Рисунок 1.4-Стенд MD1 Стенд MD1 предназначен для проверки без непосредственной установки на ...

5.6 Назначение размеров измененного сечения

Ширина измененного сечения

b _f ^‘ = (0,5 – 0,6) * b_f =(0,5 – 0,6) * 450 = 225 – 270 мм

Принимаем b _f ^‘ = 250 мм

Окончательные размеры измененного сечения:

стенка A_w = h_w * t_w = 130*1 = 130см² ;

пояс A’ _f = t_f * b_f ‘ = 2,0 * 25 = 50 см² .

Геометрические характеристики сечения

h _б = h_w + 2 * t_f = 130+2*2,0 = 134 см;

A _f ‘ = 50 см² ;

A _w = 130 см² ;

А’ = 2 * A _f ‘ + A_w = 2*50+130 = 230 см² ;

A _f ‘ / A_w = 50 / 130 = 0,385;

Статический момент пояса

S _f ‘ = A_f ‘ * z = 50*66 = 3300 cм³ ;

Статический момент половины сечения

S _0,5 ‘ = S_f ‘ + S_0,5*w = S_f ‘ + 0,5 * 0,25 * t_w * h_w ² = 3300+0,5*0,25*1*130² = 5410 cм³ ;

Момент инерции стенки

I _w = t_w * h_w ³ / 12 = 1*130³ / 12 = 183 *10³ см⁴ ;

Момент инерции поясов

2 * I’ _f = 2*A_f ^‘ * z² = 2*50*66² = 436 *10³ см⁴ ;

Момент инерции измененного сечения

I _х ’= I_w + 2 * I’_f = 183*10³ +436*10³ = 619 * 10³ см⁴ ;

Момент сопротивления измененного сечения

W _x = I_x ‘ / (0,5 * h_б ) = 619*10³ / (0,5*134) = 9240 см³ .

Таблица 2

Геометрические характеристики сечений

Основное сечение Измененное сечение

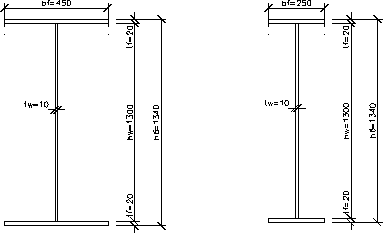
5.7 Определение места изменения сечения

Предельный изгибающий момент для измененного сечения в месте стыкового шва пояса

Расчетное сопротивление сварного шва сжатию, растяжению и изгибу по пределу текучести для полуавтоматической сварки и физических методов контроля качества шва R _wy = R_y = 2350 кг/см² (по таблице 3 СНиП II – 23 – 81*).

[M] = R _wy * W_x ‘ = 2350*9240 = 217*10⁵ кг*см = 217 т*м

По эпюре изгибающих моментов (пункт 5.1) определяем, что сечения с изгибающим моментом М = 235 т*м находятся во II и V отсеках.

Положение сечений с М = 235 кг*м относительно опор А и В

М _I = ( R_A – 0,5 * P ) * X_лев — P *( X_лев – a) = [M] →

Деформация сдвига. Геометрические характеристики плоских сечений. ...

... (срез). ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ, При деформациях кручения и изгиба, Статические моменты сечения. Центр масс сечения, Статическим моментом сечения , (6) A i . (7) Размерность статических моментов – длина в кубе. Статические моменты могут быть положительными, отрицательными ...

→ X _лев = ( [M] – Ра )/ 1,5 * P = (217- 38,8*1,9)/ (1,5*38,8) = 2,46м

Так как нагрузка симметричная, то X _лев = X_пр = 2,46 м.

Сечения отстоят от ближайших ребер на

|2,46 – 1,90|= 0,56 м = 56 см > 10 * t _w = 10*1 = 10 см → прочность обеспечена.

5.8 Проверки принятых сечений

5.8.1. По I группе предельных состояний

а) Проверка прочности основного сечения по нормальным напряжениям в месте действия максимального момента

σ = M _max / ( W_x * γ_c ) = 332*10⁵ /(14430*1,0) = 2320 кг/см² < R_y = 2350 кг/см² → прочность обеспечена

б) Проверка прочности измененного сечения по касательным напряжениям на опоре

τ = 1,5 * Q _max / ( t_w * h_w ) = 1,5*97*10³ / (1,0*130) = 1119 кг/см² < R_s = 1360 кг/см² → прочность обеспечена.

в) Проверка прочности измененного сечения по приведенным напряжениям в месте изменения сечения

σ = M * 0,5 * h _w / I_x ‘ = 217*10⁵ * 0,5*130 / (619*10³ ) = 2280 кг/см²

τ = Q _{x = х лев} / ( t_w * h_w ) = 58,2*10³ / (1*130) = 432 кг/см²

σ _пр = √ σ² + 3 *τ² = √ 2280² +432² = 2350 кг/см² < 1,15 * R_y * γ_c = 1,15*2350*1,0 = 2700 кг/см² → → прочность обеспечена

г) Проверка общей устойчивости балки

Согласно пункту 5.16 СНиП II – 23 – 81* : l _ef = a = 190 см;

b = b _f ‘ = 25 см;

t = t _f ‘ = 2 см;

• h = 2* z = 2*66 = 132 см.

Расчетное сопротивление материала R _y = 2350 кг/см² .

l _ef / b ≤ ( 0,41 + 0,0032*b / t + ( 0,73 – 0,016 * b / t ) * b / h ) * √ Е / R_y

190/25 = 7,6 < (0,41+0,0032*25/2+(0,73-0,016*25/2)*25/132)*√2,1*10 ⁶ /2350 = 16,4 → общая устойчивость обеспечена

5.8.2. По II группе предельных состояний по деформативности при нормальных условиях эксплуатации

Коэффициент, учитывающий уменьшение жесткости балки вследствие перемены сечения, 0,9.

f / L = 0,1 *M ^н _max * L / ( 0,9 * E * I_x ) = 0,1 *M_max * L / ( 0,9 * E * I_x ) * q^н / q =

= 0,1*332*10 ⁵ *11.2*10² / (0,9*2,1*10⁶ *967*10³ ) * 5.61/6.68 = 1/588 < [ f / l ] = 1/400 → прочность обеспечена

5.9 Проверки местной устойчивости

5.9.1. Проверка местной устойчивости пояса

b _ef / t_f ≤ 0,5 * √ E / R_y

Величина неокаймленного свеса

b _ef = 0,5*(45-1) = 22 см

22 / 2,0 = 11 < 0,5*√ 2,1*10 ⁶ / 2350 = 14,9 → устойчивость пояса обеспечена

5.9.2. Проверка местной устойчивости стенки

а) Расстановка ребер жесткости

Отчет с рис табл источника

... Сварка титановых сплавов Для сварки титановых сплавов применяют следующие виды сварки: электронно-лучевая сварка, холодная сварка, прессованная сварка, плазменная сварка, дуговая сварка ... Для предупреждения пор необходимо прежде всего обеспечить удаление с поверхности свариваемых кромок и ... технически чистый титан двух марок (табл. 1.1) [5]. Таблица 1.1 – Химический состав технически чистого ...

Предусматриваем парные поперечные (вертикальные) ребра в местах опирания балок настила и на опорах.

Так как λ _w = 4,35 > 3,2 , то согласно пункту 7.10 СНиП II – 23 – 81*, расстояние между ребрами

а = 190 (180) см < 2 * h _ef = 2*130 = 260 см → условие выполнено.

б) Определение размеров промежуточных ребер по СНиП II – 23 – 81*

Требуемая ширина

b _h ^тр = h_ef /30 + 40 = 1300/30+40 = 83.3 мм

Принимаем b _h =90 мм > b_h ^тр =83.3 мм

Требуемая толщина ребра

t _s ^тр = 2 * b_h * √ R_y / E = 2*90*√ 2350 / (2,1*10⁶ ) = 6,02 мм

Тогда b _h х t_s = 90 х 7 мм

Так как принято сопряжение на одном уровне, то размеры ребра : b _h = 110 мм;

t _s = 10 мм.

Принимаем b _h х t_s = 110 х 10 мм.

в) Проверка местной устойчивости стенки

Так как λ _w = 4,35 > 3,5, то проверяем местную устойчивость.

1. Проверка устойчивости стенки в I отсеке

При а/ h _ef =190(180)/130=1.46(1,38)>1 расчётная длина l^р _отс = h_ef =130см

Так как во I отсеке сечение балки не меняется, то вычисляем изгибающий момент М и поперечную силу Q на расстоянии Х ₁ = а – h_w / 2 = 1,8 – 0,5*1,30 = 1,15м.

Поперечная сила

Q _{х =} = 97 т

Изгибающий момент

М _{х =1,15} = ( R_A – P / 2 ) * Х₁ = Q_max * x₁ = 97*1,15 = 111,5 тм

Нормальное напряжение

σ = M _{х =1,15} * 0,5 * h_w / I_x ‘ = 111,5*10⁵ * 0,5*130 / (619*10³ ) = 1171 кг/см²

Касательное напряжение

τ = Q _{x = 1,155} / ( t_w * h_w ) = 97*10³ / (1,1*130) = 746 кг/см²

Нормальное критическое напряжение для I отсека

C _cr = 30,0 (по таблице 21 СНиП II – 23 – 81*).

σ _cr = C_cr *R_y / λ_w ² = 30,0*2350 / 4,35² = 3730 кг/см²

Касательное критическое напряжение для I отсека

Отношение большей стороны отсека к меньшей μ = a / h _w = 180/130 = 1,38.

Меньшая из сторон отсека d = h _w =130 см.

λ _ef = d / t_w * √ R_y / E = 130/1*√2350/(2,1*10⁶ ) = 4,35

τ _{с r} = 10,3 * ( 1 + 0,76 / μ² ) * R_s / λ_ef ² = 10,3*(1+0,76 / 1,38² )*1360 / 4,35² = 1035 кг/см²

Проверка устойчивости

√ ( σ / σ _cr )² + ( τ / τ_cr )² = √ ( 1171 / 3730)² + ( 746 /1035 )² = 0,786 < γ_с = 1 → местная устойчивость в I отсеке обеспечена.

2. Проверка устойчивости стенки во II отсеке

Во II отсеке балка меняет сечение. В месте изменения сечения максимальное нормальное напряжение в стенке.

Расчет балочной площадки

... курсовой работе можно принимать = с=1,10 см3 Из сортамента подбираем ближайший профиль, меньший по массе, у которого выполняется условие Принимаем двутавр № 40Б1 803,6 ? 696,88 - условие ... балочный площадка колонна сечение где б = 1,01-1,03 - коэффициент учитывает вес балки, сечение которой, на данном этапе расчета, ... в одной ячейке балочной площадки усложненного варианта кг/м2 Таблица 1.1 - Сравнение ...

σ = M _{х =2,47} * 0,5 * h_w / I_x ‘ = 2044 кг/см²

τ = Q _х=2,47 / ( t_w * h_w ) = 448 кг/см²

Так как рассчитываемый отсек имеет те же размеры, что и отсек I, кроме длины, не влияющей на расчет, считаем, что критические напряжения имеют те же значения, тогда:

√ ( 2044 / 3730) ² + ( 448 / 1035 )² = 0,55 < γ_с = 1

3. Проверка устойчивости стенки в III отсеке

Устойчивость обеспечена, так как касательное напряжение t меньше.

5.10 Расчет поясных швов

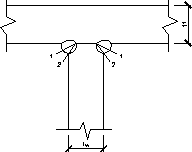
1 – 1 – сечение по металлу шва;

2 – 2 – сечение по металлу границы сплавления.

1. Расчет по металлу шва.

Катет шва

Согласно пункту 12.8 СНиП II – 23 – 81* катет шва K _f ≤ 1,2 * t_w = 1,2*1 = 1,2 см.

По таблице 38* СНиП II – 23 – 81* для автоматической сварки при 17 мм < t _f = 20 мм < 22мм катет шва K_f ≥ 6 мм.

Принимаем минимально возможное значение K _f = 6 мм.

По таблице 34* СНиП II – 23 – 81* принимаем автоматическую сварку в «лодочку» при диаметре проволоки d = 1,4 – 2 мм для катета шва K _f = 6 мм.

Коэффициенты, учитывающие форму поперечного сечения шва β _f = 0,9;

β _z = 1,05.

Коэффициенты условий работы шва γ _wf = γ_wz = 1,0 (пункт 11.2 СНиП II – 23 – 81*).

По таблице 55* СНиП II – 23 – 81* для района II ₅ , 2-ой группы конструкций и стали С235 принимаем материалы дла сварки: флюс – АН – 348 – А ( по ГОСТ 9087 – 81*);

• сварочная проволока СВ – 08А ( по ГОСТ 2248 – 70*).

Расчетное сопротивление углового шва срезу по металлу шва

Нормативное сопротивление металла шва по временному сопротивлению R _wun = 4200 кг/см² ( по таблице 4* СНиП II – 23 – 81*).

Коэффициент надежности по металлу шва γ _wm = 1,25 ( по таблице 3*, примечание 3, СНиПII–23–81*).

R _wf = 0,55 * R_wun / γ_wm = 0,55*4200/1,25 = 1850 кг/см²

Расчетное сопротивление по металлу границы сплавления

Временное сопротивление стали разрыву R _un = 3600 кг/см² (по таблице 51* СНиП II – 23 – 81*).

R _wz = 0,45 * R_un = 0,45*3600 = 1620 кг/см²

Условие (*)

1,0 ≤ R _wf / R_wz ≤ β_z / β_f (*)

1,0 < 1848/1620 = 1,14 < 1,05/0,9 = 1,17 → условие выполнено.

Так как условие выполнено, то материал для сварки подобран правильно.

Проверка прочности по металлу шва

Сдвигающее усилие на единицу длины:

T = Q _max * S_f ‘ / I_x ‘ = 97*10³ * 3300 / (619*10³ ) = 517 кг.

τ _f = T / (2 * β_f * K_f ) = 517 / (2*0,9*0,6) = 478 кг/см² < R_wf * γ_wf * γ_c = 1850*1,0*1,0 = 1850 кг/см² → прочность по металлу шва обеспечена.

2. Расчет по металлу границы сплавления.

Так как условие (*) выполнено, и прочность по металлу шва обеспечена, то при γ _wf = γ_wz = 1,0 расчет прочности по металлу границы сплавления даст заведомо положительный результат.

5.11 Расчет опорных ребер

5.11.1. Конструкция ребер на опорах А и Б.

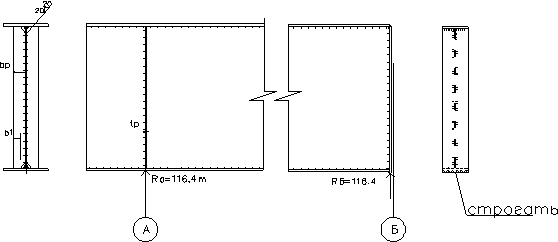
5.11.2. Определение размеров опорных ребер из условия прочности на смятие.

Требуемая ширина ребра на опоре по оси А

b _р ^тр = (b_f ‘ – t_w ) / 2 = (25-10) / 2 = 12 см = 120 мм

Принимаем b _р = 120 мм.

Длина площадки смятия ребра

b ₁ = 1 / 2 *(b_f ‘ – 2 *2,0 — t_w ) = 1/2 *(25-2*2,0-1,0) = 10 см

Требуемая толщина ребра по оси А из условия прочности на смятие

Коэффициент надежности по материалу γ _m = 1,025 (по таблице 2* СНиП II – 23 – 81*).

Расчетное сопротивление смятию торцевой поверхности при наличии пригонки

R _p = R_un / γ_m = 3600/1,025 = 3512,2 кг/см² .

t _p ^тр = R_A / (R_p * 2 * b₁ ) = 116*10³ / (3512,2*2*10) = 1,58 см

По ГОСТ 82 – 70* принимаем t _p = 1,6 см > t_p ^тр = 1,58 см.

Для ребра по оси Б назначаем такую же толщину t _p = 1,6 см, а ширину b_р = b_f ‘ = 25 см, тогда площадь смятия для этого ребра будет больше, чем по оси А, и прочность на смятие заведомо обеспечена.

5.11.3. Расчет опорных ребер на устойчивость в плоскости, перпендикулярной стенке.

S = 0,65 * t _w * √ E / R_y = 0,65*1,0*√2,1*10⁶ /2350 = 19,4 см

Так как расчетное сечение по оси Б имеет меньшую площадь, то проверяем устойчивость ребра по оси Б.

A = S * t _w + b_f ‘ * t_p = 19,4*1,0+25*1,6 = 59,4 см²

I _x = t_p * (b_f ‘)³ /12 = 1,6*25³ / 12 = 2083 см⁴

i _x = √ I_x / A = √ 2083 / 59,4 = 5,92 см

λ _x = h_w / i_x = 130/5,92 = 22

φ ≈ 0,956 (по таблице 72* СНиП II – 23 – 81*)

σ = R _Б / (φ * А) = 116*10³ / (0,956*59,4) = 1960 кг/см² < R_y = 2350 кг/см² → устойчивость опорных ребер обеспечена.

5.11.4. Расчет сварного шва, соединяющего спарное ребро по оси Б со стенкой.

По таблице 34* СНиП II – 23 – 81* принимаем полуавтоматическую сварку в углекислом газе проволокой диаметром d < 1,4 мм при нижнем положении шва.

Коэффициенты, учитывающие форму поперечного сечения шва β _f = 0,7;

β _z = 1,0.

Коэффициенты условий работы шва γ _wf = γ_wz = 1,0 (пункт 11.2 СНиП II – 23 – 81*).

По таблице 55* СНиП II – 23 – 81* для района II ₅ , 2-ой группы конструкций и стали С235 принимаем сварочную проволоку СВ – 08Г2С ( по ГОСТ 2246 – 70*).

Расчетное сопротивление углового шва срезу по металла шва

Нормативное сопротивление металла шва по временному сопротивлению R _wun = 5000 кг/см² (по таблице 4* СНиП II – 23 – 81*).

Коэффициент надежности по металлу шва γ _wm = 1,25 ( по таблице 3*, примечание 3 , СНиП II – 23 –81*).

R _wf = 0,55 * R_wun / γ_wm = 0,55*5000/1,25 = 2200 кг/см²

Расчетное сопротивление по металлу границы сплавления

R _wz = 0,45 * R_un = 0,45*3600 = 1620 кг/см²

Условие (*)

1,0 ≤ R _wf / R_wz ≤ β_z / β_f

1,0 < 2200/1620 = 1,36 < 1,0/0,7 = 1,43 → условие выполнено.

Требуемая высота катета шва

K _f ^тр = √ R_Б / (2 * 85 * β_f ² * R_wf ) = √ (116 *10³ ) / (2*85*0,7² *2200) = 0,775 см

Принимаем K _f = 0,8 см > K_f ^тр = 0,775 см.

При t _p = 16 мм K_f = 0,8 см > K_{f , min} = 0,5 см и K_f = 0,8 см < K_{f , mах} = 1,2 * t_w = 1,2*1 = 1,2 см → условие выполнено.

5.12 Расчет монтажного стыка на высокопрочных болтах

5.12.1. Предварительная разработка конструкции.

Предварительно принимаем диаметр высокопрочных болтов d _b = 20 мм.

Площадь сечения нетто болта A _bn = 2,45 см² .

Диаметр отверстия

d = d _b + 3 = 20+3 = 23 мм.

Из конструктивных соображений принимаем толщину накладки для стенки t _н = t_w =1,0 см.

Зазор между отправочными марками в стыке 10 мм.

Число вертикальных рядов в стенке по одну сторону от стыка n = 2.

Минимальное расстояние между рядами

2,5 * d = 2,5*23 = 57,5 мм ≈ 60 мм.

Расстояние от края стенки или накладки до ближайшего ряда

1,3 * d = 1,3*23 = 29,9 мм ≈ 30 мм.

Шаг болтов по вертикали

/ 4 + 6 / * d = /4 + 6/*23 = 92 + 138 мм.

Шаг болтов принимаем 100 мм.

Расстояние между крайним болтом в вертикальном ряду и внутренней гранью пояса

60 мм < с = 100 < 120 мм.

Толщина накладок в поясе > 0,5 * t _f = 0,5*2,0 = 1,2 см.

Расстояние между внутренними накладками d ₁ ≥ 40 мм.

Для пояса принимаем четырехрядное расположение болтов.

5.12.2. Определение места стыка.

Момент инерции ослаблений (отверстиями) сечения пояса

I _f ^осл = A_f ^осл * z² = 4 * d * t_f * z² = 4*2,3*2,0*66,0² = 80,2 * 10³ см⁴

Момент инерции ослаблений сечения стенки

∑ l _i ² = l₁ ² + l₂ ² + l₃ ² + l₄ ² + l₅ ² = 10² (1² +3² +5² +7² +9² +11² ) = 28600см²

I _w ^осл = 2 * d * t_w * (∑ l_i / 2)² = d * t_w * ∑ l_i ² / 2 = 2,3*1*28600 / 2 = 32,9 * 10³ см⁴

Момент инерции ослаблений всего сечения

I ^осл = 2 * I_f ^осл +I_w ^осл = (2*80,2+32,9)*10³ = 193 * 10³ см⁴

Момент инерции сечения с учетом ослаблений (нетто)

I _n = I_x – I^осл = (967-193)*10³ = 774 * 10³ см⁴

Так как I _n / I_x = 774 * 10³ / (967 * 10³ ) = 0,80 < 0,85, то в соответствии с п. 11.14 [I] условный момент инерции сечения нетто

I _с = 1,18*I_n = 1,18*774 * 10³ =913*10³ см⁴

Условный момент сопротивления

W _c = I_c / (0,5 * h_б ) = 913*10³ / (0,5*134) = 13630 см³

Предельный изгибающий момент в месте монтажного стыка

[M] = W _c * R_y = 13630*2350 = 320 * 10⁵ кг*см = 320 т*м

По эпюре изгибающих моментов определяем, что сечение с изгибающим моментом, равным предельному ([M] = 320 т*м), находится во III и IV отсеках. Принимаем, что стык будет в III отсеке.

Положение стыка

Из уравнения М _III для III определим положение стыка X_ст

М _III = (R_A – 0,5*Р) X_ст – Р(X_ст -а)- Р(X_ст -2а) = [М]

2,0Р* X _ст –2* Р* X_ст +3*Ра = [М]

X _ст = ([М]- 3*Р*а)/0,5Р = (320-3*38,8*1,9)/0,5*38,8=5,09 м. Расстояние от ближайшего поперечного ребра жёсткости 0,91 м > 0,5 м. Окончательно принимаем стык на расстоянии X_ст = 5,09м.

Внутренние усилия в месте стыка: изгибающий момент М _х=5,09 = 320 т*м;

поперечная сила Q _х=5,09 = 19,4 т.

5.12.3. Расчет стыка стенки.

Момент, воспринимаемый стенкой

Момент инерции стенки с учетом ослаблений (нетто)

I _wn = I_w – I_w ^осл = (183-32,9)*10³ = 150,1 * 10³ см⁴

M _w = М_х=5,47 * I_wn / I_n = 320*150,1*10³ / (774*10³ ) = 62,0 т*м

Поперечная сила, воспринимаемая стенкой

Q _w = Q_х=5,09 = 19,4 т.

Усилие, приходящее0ся на крайний болт вертикального ряда от момента M _w

N _M = M_w * l_max / (n * ∑ l_i ² ) = 62*10⁵ *110 / (2*28600) = 11920 кг

Усилие, приходящееся на крайний болт вертикального ряда от поперечной силы Q _w

Число болтов в вертикальном ряду m = 12 шт.

N _Q = Q_w / (n * m) = 19,4*10³ / 2*12 = 808кг

Суммарное усилие, приходящееся на крайний болт вертикального ряда

N _b = √ N_M ² + N_Q ² = √ 11920² +808² = 11947 кг = 11,95 т

Предельное усилие многоболтового соединения, приходящееся на один болт

По таблице 61* СНиП II – 23 – 81* для высокопрочных болтов принимаем сталь 40Х «Селект».

Наименьшее временное сопротивление материала болта разрыву R _bun = 11000 кг/см² .

Количество плоскостей трения n ^тр = 2.

Коэффициент условия работы соединения при количестве болтов ³ 10 γ _b = 1,0 (пункт 11.13 СНиП II – 23 – 81*).

Коэффициент трения при газопламенном способе обработки соединяемых поверхностей μ = 0,42 (по таблице 36* СНиП II – 23 – 81*).

Коэффициент условия работы балки в месте стыка на высокопрочных болтах γ _с = 1,0 (по таблице 6* СНиП II – 23 – 81*).

Коэффициент надежности при газопламенном способе обработки и регулировании натяжения болтов по моменту закручивания γ _h = 1,12 (по таблице 36* СНиП II – 23 – 81*).

[N _b ] = 0,7 * R_bun * n^тр * γ_b * A_bn * μ * γ_с * 1/γ_h = 0,7*11,0*2*1,0*2,45*0,42*1,0*1/1,12 = 14,14т>N_b =11,95т → условие выполнено.

(14,14 – 11,95) / 11,95 *100% =18 % » 20 % → условие выполнено.

5.12.4. Расчет стыка пояса.

а) Определение числа болтов в стыке пояса.

Момент, воспринимаемый поясами

M _f = M_{x =5,09} – M_w = 320-62 = 258 т*м

Продольное усилие в поясе

N _f = M_f / (2 * z) = 258 / (2*0,66) = 196 т

Требуемое число болтов (по одну сторону от стыка)

n _b ^тр = N_f / [N_b ] = 196/14,14 = 13,86 шт.

Принимаем 14 болтов.

б) Проверка прочности накладок.

Пусть толщина накладок в поясе t _н = 12 мм > 0,5 * t_f = 0,5*20 = 10 мм.

Ширина наружной накладки b _н = b_f = 450 мм.

Ширина внутренней накладки

b _н ‘ ≤ 0,5 * (b_f — 40) = 0,5*(450-40) = 205 мм

Принимаем b _н ‘ = 200 мм.

Расстояние между внутренними накладками

d ₁ = b_н – 2 * b_н ‘ = 450-2*200 = 50 мм > 40 мм → условие выполнено.

Площадь сечения накладок

A _н = t_н * (b_н +2*b_н ‘) = 1,2*(45+2*20) = 102 см² > A_f = t_f * b_f = 2,0 * 45 = 90 см² → прочность накладок обеспечена.

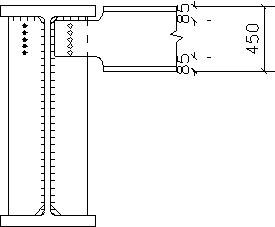
Окончательно принятая конструкция

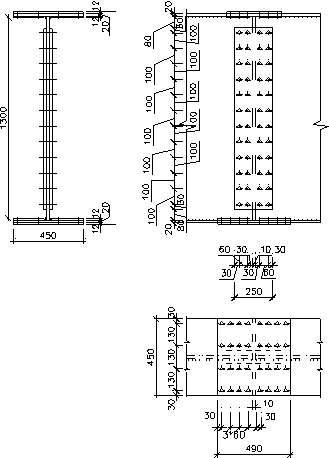
6. Конструкция и расчет прикрепления

балки настила к главной балке.

Принимаем по табл.57, что на балке настила присоединяется к ребру главной балки на болтах грубой точности класса 4.6.

Пусть диаметр болтов d _b = 22 мм, а диаметр отверстия d = d_b + 3 = 22 + 3 = 25 мм.

Расчетное усилие, которое может быть воспринято одним болтом на срез, по формуле:

N _bs = R_bs *g_b *A_b *n_s

N _bs = 1500*0.9*3.8*1 = 5130 кг,

Где R _bs – расчетное сопротивление болтового соединения срезу;

g _b — коэффициент условий работы соединения в расчетах на срез,

A _b = П*d² _b /4 = 3.8 см² – площадь сечения стержня болта брутто,

n _s — число расчетных срезов одного болта.

Расчетное усилие, которое может быть воспринято одним болтом при работе соединения на смятие, по формуле:

N _{b р} = R_{b р} *g_b *d_b *St_min

N _{b р} = 3550*0.9*2.2*0.76 = 5340 кг

Где R _{b р} – расчетное сопротивление болтового соединения смятию;

St _min — наименьшая суммарная величина элементов, сминаемых в одном направлении,

St _min = t_w = 0.76 см < t_s = 1.0 см, где t_w и t_s –толщина стенки балки настила и промежуточного ребра главной балки соответственно.

Количество болтов

n = 1.2*R/N _min = 1.2*18.2*10³ /5130 = 4.25,

где R – величина опорной реакции балки настила,

1,2 – коэффициент, учитывающей влияние защемления в соединениях,

N _min – меньшее значение из величин N_bs и N_bp .

Принимаем 5 болтов. Так как значения a и b соответствуют требованиям, корректировать значение g _b при определении N_bp не требуется.

Проверка стенки балки настила на срез по ослабленному отверстиями и вырезами сечению:

t = R/A _n = 18.2 *10³ / 19.4 = 940 кг/см² < R_s *g_s = 1420*1 = 1420 кг/см²

7. Расчет колонны К1

7.1 Расчетная схема, определение нагрузки, статический расчет

Нагрузка на колонну

Коэффициент, учитывающий вес колонны, 1,005.

N = 2 * R _Б * 1,005 = 2*116*1,005 = 232 т

Приближенное значение нагрузки на колонну

Коэффициент, учитывающий вес балок и колонны, 1,04.

N = g * (L ₁ + L₂ ) / 2 * (l₁ + l₂ ) / 2 * 1,04 = 3,46 * (11,2+11,2)/2 * (5,7+5,7)/2 * 1,04 = 230 т

Отметка верха колонны

Отметка настила (пола) площадки d _н = 8,4 м.

Толщина стяжки t _стяжки = 0,025 м.

Толщина железобетонной плиты t _{ж/б плиты} = 0,10 м.

Высота сечения главной балки h _{гл.балки} = 1,34 м.

Величина выступа опорного ребра главной балки 0,015 м.

d _в.к = d_н – (t_стяжки + t_{ж/б плиты} + h_{гл.балки} + h_Б1 + 0,015) = 8,4-(0,025+0,10+1,34+0,015) = 6,92 м

Длина колонны

Отметка низа колонны d _н.к = -0,4 м

l _к = d_в.к – d_н.к = 6,92 – (-0,4) = 7,32 м

Расчетная схема колонны

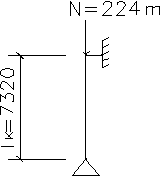
Расчетные длины относительно обеих главных осей

l _x = l_y = l_ef = μ * l_к = 1 * 7,32 м

7.2 Подбор сечения и проверка устойчивости колонны

7.2.1. Определение сечения вервей.

Принимаем сквозную колонну из двух прокатных швеллеров, соединенных планками.

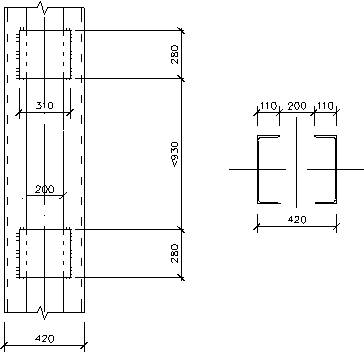
По таблице 50* СниП II – 23 – 81* для колонны К1, относящейся к 3-й группе конструкций, принимаем сталь марки С245 (ГОСТ 27772 — 88).

По таблице 51* СниП II – 23 – 81* для фасонного проката из стали марки С245 при толщине 4 – 20 мм расчетное сопротивление материала пояса по пределу текучести R _y = 2450 кг/см² .

Так как ослабления в колонне отсутствуют (А _н = А), расчет на прочность не требуется; определяющим является расчет на устойчивость

Сечения ветвей из расчета на устойчивость относительно материальной оси Х – Х.

Задаемся гибкостью λ _х ^з = 60.

Коэффициент продольного изгиба центрально — сжатых элементов φ _х ^з = 0,805 (таблица 72* СниП II – 23 – 81*).

Требуемый радиус инерции

i _x ^тр = l_x / λ_х ^з = 732/ 60 = 12,2 см.

А _В ^тр = N / (2 * φ_х ^з * R_y * γ_c ) = 232 * 10³ / (2*0,805*2450*1,0) = 56,8 см²

По сортаменту принимаем швеллер № 36 с площадью поперечного сечения А _В = 53,4 см² » А_В ^тр = 56,8 см²

Геометрические характеристики: А _В = 53,4 см² ;

i _x = 14,2см; b_f = 11,0см; I_{y 1} = 513 см⁴ ; i_{y 1} = 3,1 см⁴ ; z₀ = 2,68 см;

t _w = 0,75 см; t_f = 1,26 см.

7.2.2. Проверка устойчивости колонны относительно материальной оси Х – Х.

Гибкость стержня

Предельная гибкость [λ] = 120 (таблица 19* СниП II – 23 – 81*).

λ _х = l_x / i_x = 732/ 14,2 = 51,5 < [λ] = 120

Коэффициент продольного изгиба центрально-сжатого стержня φ _х = 0,86 ( таблица 72*СниП II–23– 81*).

σ = N / (2 * A _B * φ_x ) = 232*10³ / (2*53,4*0,86) = 2430 кг/см² < R_y * γ_c = 2450*1,0 = 2450 кг/см² → устойчивость колонны относительно материальной оси Х – Х обеспечена.

Недонапряжение (2450-2430) / 2450 *100% = 0,8%.

Окончательно принимаем 2 швеллера № 36 .

7.2.3. Установление расстояния между ветвями.

Гибкость ветви относительно оси Y – Y.

λ _в £λ_х / √2 = 51,5 / √2 = 36,5

Принимаем λ _в = 30, тогда λ_y ^тр = √ λ_х ² — λ_в ² = √ 51,5² — 30² = 41,1 > λ_в = 30

Требуемый радиус инерции

i _y ^тр = l_y / λ_y ^тр = 732/ 41,1 = 18,1 см.

Требуемое расстояние между центрами тяжести ветвей

с ^тр = 2 * √ (i_y ^тр )² — i_{y 1} ² = 2*√ 18,1² – 3,1² = 35,67 см

Требуемая ширина колонны

b _к ^тр = c^тр + 2 * z₀ = 35,67+2*2,68 = 41,03 см

Приближенное значение ширины колонны (Коэффициент формы сечения α = 0,44.)

b _к ^тр = i_y ^тр / α = 18,1 / 0,44 = 41,1 см

Принимаем b _к = 42 см.

Зазор между ветвями

d = b _к – 2 * b_f = 42 – 2*11 = 20 см > 10 см → условие выполнено.

Так как условие выполнено, оставляем принятый размер b _к = 42 см.

Расстояние между центрами тяжести ветвей

с = b _к – 2 * z₀ = 42 – 2*2,68 = 36,67 см

7.2.4. Проверка устойчивости относительно свободной оси Y – Y.

I _y = 2 * (I_{y 1} + A_В * (0,5 * с)² ) = 2 * (513 + 53,4*(0,5*36,7)² ) = 38850 см⁴

ⁱ _y = √ I_y / (2 * A_В ) = √ 3 / (2*53,4) = 19,07 см > i_y ^тр = 18,1 см → условие выполнено.

λ _y = l_y / i_y = 732 / 19,07 = 38,4 > λ_в = 30 → условие выполнено.

Приведенная гибкость относительно свободной оси Y – Y.

λ _ef = √ λ_y ² + λ_в ² = √ 38,4² + 30² = 49,7 ≈ λ_x = 50,7

Так как λ _ef = 49,7 < λ_x =50,7 то φ_х = 0,87 < φ_y = 0,871 и устойчивость относительно оси Y – Y можно не проверять.

7.3 Расчет соединительных планок

7.3.1. Установление размеров планок.

d = (0,5 – 0,75) * b _к = (0,5 – 0,75)*42 = 21 – 32 см

Принимаем d = 25 см.

Длина планки

b _S = d +2 * 4 = 21 + 2*4 = 29 см

Требования:

Принимаем t = 1.

d / t = 25 / 1 = 25 < 30 → условие выполнено.

b _S / t = 29 / 1 = 29 < 50 → условие выполнено.

Так как условия удовлетворены, то выпучивания быть не должно.

Требуемое расстояние между планками

l _В ^тр = λ_в *ⁱ _y1 = 30*3,1 = 93 см

Требуемое расстояние между осями планок

l ^тр = l_В ^тр + d = 93 + 25 = 118 см

I _S = t * d³ / 12 = 1*25³ / 12 = 1300 см⁴

I _В = I_{y 1} = 513 см⁴

I _S * l / (I_В * с) = 1300*118 / (513*37,64) = 7,82 > 5 → условие выполнено.

7.3.2. Определение усилий в планках.

Фиктивная поперечная сила

Коэффициент β

Так как φ _х = 0,87 < φ_y = 0,871, то φ_min = φ_х = 0,87.

φ _min / φ_y = 0,87 / 0,871 = 0,9999=1

N / (φ _y * 2 * A_B * R_y ) = 224 * 10³ / (0,871*2*53,4*2450) = 0,975

Так как φ _min / φ_y = 1 > N / (φ_y * 2 * A_B * R_y ) = 224*10³ / (0,871*2*53,4*2450) = 0,975 то β = 0,975.

Q _fic = 7,15 * 10^-6 * 2 * A_B * E * β * (2330 * R_y / E – 1 ) =

= 7,15 * 10 ^-6 * 2 * 53,4 * 2,1 * 10⁶ * 0,975 * (2330 * 2450 / (2,1 * 10⁶ ) – 1) = 2690 кг

Приближенное значение фиктивной поперечной силы (в запас) по методу интерполяции

При R _y = 2450 кг/см²

Q’ _fic = (20 + (30 – 20) / (2600 – 2100) * (2450 – 2100)) * 2 * A_B =

= (20 + (30 – 20) / (2600 – 2100) * (2450 – 2100)) * 2 * 53,4 = 2880 кг

Поперечная сила, действующая в плоскости планок

Q _S = Q_fic / 2 = 2690 / 2 = 1345 кг

Сила, срезывающая одну планку

F = Q _S * l / c = 1345*118 / 37,64 = 4220 кг

Момент, изгибающий планку в ее плоскости

М ₁ = Q_S * l / 2 = 1345*118 / 2 = 79300 кг*см

7.3.3. Проверка прочности приварки планок.

Предусматриваем использование ручной сварки при изготовлении колонны. Принимаем, что планки прикрепляются к полкам швеллеров угловыми швами с высотой катета K _f = 8 мм < t = 10 мм с заводкой швов за торец на 20 мм.

По таблице 55* СниП II – 23 – 81* для района ll ₅ и стали марки С245 принимаем электроды марки Э42 (ГОСТ 9467 – 75).

Коэффициенты, учитывающие форму поперечного сечения шва β _f = 0,7; β_z = 1,0.

Коэффициенты условий работы шва γ _wf = γ_wz = 1,0 (пункт 11.2 СНиП II – 23 – 81*).

R _wf = 1850 кг/см² (таблица 56* СниП II – 23 – 81*).

Временное сопротивление для толщины проката 11см < t _f = 12,6 см < 20 мм R_un = 3700 кг/см² (таблица 51* СниП II – 23 – 81*).

R _wz = 0,45 * R_un = 0,45*3700 = 1665 кг/см²

1,1 < R _wf / R_wz = 1850 / 1665 = 1,11 < β_z / β_f = 1,0 / 0,7 = 1,43 → условие выполнено.

Напряжение в шве

τ _F = F / (β_f * K_f *a) = 4220 / (0,7*0,8*25) = 301 кг/см²

τ _{М 1} = 6 * М₁ / (β_f * K_f *a² ) = 6*79300 / (0,7*0,8*25² ) = 1360 кг/см²

Условие прочности шва

τ = √ τ _F ² + τ_{M 1} ² = √ 301² + 1360² = 1390 кг/см² < R_wf * γ_wf * γ_c = 1850 * 1,0 * 1 = 1850 кг/см² → прочность шва обеспечена с большим запасом.

Уменьшаем катет шва до K _f = 6 мм.

τ = 1390 *0,8/0,6 = 1850 кг/см ² < R_wf * γ_wf * γ_c = 1850 * 1,0 * 1 = 1850 кг/см² → прочность обеспечена.

Прочность планок заведомо обеспечена, так как толщина планки t = 10 мм > K _f = 6 мм.

7.4 Расчет базы

7.4.1. Определение размеров плиты в плане.

Расчетное сопротивление смятию бетона фундамента.

Принимаем ξ = ³ √ А_ф / А_пл = 1,2

Призменная прочность бетона М150 R _с = 70 кг/см²

R _ф = ξ * R_с = 1,2*70 = 84 кг/см²

Требуемая площадь плиты

А _пл ^тр = N / R_ф = 232*10³ / 84 = 2760 см²

Ширина плиты из конструктивных соображений

Принимаем с = 5 см.

В _пл = h_к + 2 * t_тр + 2 * c = 36 + 2*1,0 + 2*5,0 = 48,0 см

Требуемая длина плиты

L _пл ^тр = А_пл ^тр / В_пл = 2760 / 48 = 57,5 см

Требуемая длина плиты из конструктивных соображений

L _пл ^тр = b_к + 2 * а₁ = 42,0 + 2*10,0 = 62,0 см

Окончательно принимаем L _пл = 62,0 см.

7.4.2. Определение толщины плиты.

Плита работает на изгиб как пластинка, опертая на траверсы и торец стержня и нагруженная равномерно распределенным (условно) реактивным давлением фундамента.

q = N / (В _пл * L_пл ) = 232*10³ / (48*62) = 74,9 кг/см² < R_ф = 84 кг/см²

Максимальные моменты для отдельных участков плиты

I участок (плита работает как пластинка, опертая по контуру)

Коэффициент, зависящий от отношения более длинной части стороны участка «а» к более короткой «b» α

а / b = 42/36 = 1,2 → α = 0,063

М _l = α * q * b² = 0,063*74,9*36² = 6115 кг*см

II участок (плита работает как пластинка, опертая по трем сторонам)

Коэффициент, зависящий от отношения закрепленной стороны «а ₁ » к незакрепленной «b₁ » α₁

а ₁ / b₁ = 10 / 36 = 0,28 < 0,5

Так как а ₁ / b₁ = 0,25 < 0,5, то плита работает как консоль вылетом а₁ = 10 см.

М _ll = 0,5 * q * а₁ ² = 0,5*74,9*10² = 3745 кг*см

III участок (плита работает как консоль)

М _lll = 0,5 * q * с² = 0,5*74,9*5,0² = 935 кг*см

По таблице 50* СниП II – 23 – 81* для плиты принимаем сталь марки ВСт3кп2 (ГОСТ 380 – 71*).

По таблице 51* СниП II – 23 – 81* для проката из стали марки ВСт3кп2 при толщине t = 21 – 40 мм расчетное сопротивление материала по пределу текучести R _y = 2100 кг/см² .

Требуемая толщина плиты

t _пл ^тр = √ 6 * M_max / (R_y * γ_c ) = √ 6*6115 / (2100*1) = 4,18 см, так как толщина плиты превышает 4см введем дополнительное ребро на участке I.

Рассмотрим участок Iа:

а= h _к = 36см. b=0,5 b_к =0,5*42=21см;

• a/b= 36/21=1,67; → α = 0,09

М _la = 0,09 *74,9*21² = 2970 кг*см

M _max = М_ll = 3745 кг*см

t _пл ^тр = √ 6 * M_max / (R_y * γ_c ) = √ 6*3745 / (2100*1) = 3,34 см

Принимаем t _пл = 36 мм > t_пл ^тр = 33,4 мм.(ближайший больший стандартный размер)

7 .4.3. Расчет траверсы.

Требуемая высота траверсы

При K _f = 1,0 см < 1,2 * t_трав = 1,2*1,0 = 1,2 см

h _трав ^тр = N / (4 * β_f * K_f * R_wf * γ_c * γ_wf ) + 1,0 = 232*10³ /(4*0,7*1,0*1850*1*1,0)+1,0 = 44 см

Принимаем h _трав = 44 см

Приближенная проверка траверсы по прочности

Нагрузка на единицу длины опорного листа траверсы

q _трав = q * В_пл / 2 = 74,9*48 / 2 = 1770 кг / см

Изгибающий момент и поперечная сила в места приварки к колонне

М _трав = 0,5 * q_трав *а₁ ² = 0,5*1770*10² = 88300 кг*см

Q _трав = q_трав *а₁ = 1770* 10 = 17650 кг

Момент сопротивления сечения листа

W _трав = t_трав * h_трав ² / 6 = 1,0*44² / 6 = 323 см³

Проверка прочности

σ = М _трав / W_трав = 88300 / 323 = 273 кг/см² < R_y * γ_c = 2100*1,0 = 2100 кг/см²

τ = Q _трав /(h_трав *t_трав ) = 17650/(44*1,0) = 400 кг/см² < R_S *γ_c = 0,58*R_y *γ_c = 0,58*2100*1,0 = 1218кг/см²

σ _пр = √σ² + 3 * τ² = √ 273² + 3*400² = 742 кг/см² < R_y * γ_c = 2100*1,0 = 2100 кг/см² → прочность траверсы обеспечена.

7 .4.3. Расчет дополнительного ребра.

Принимаем толщину ребра t _р = 1,0см

N _p = q* b_к / 2 * h_к =74,9 * 42/2 *36= 57200кг.

Принимаем высоту катета K _f = 1,0 см

Из условия прочности швов:

h _к ^тр = N_p /4* β_f * K_f * R_wf * γ_c * γ_wf )= 57200 / (4*0,7*1,0*1850*1,0*1,0)=11,05 см

Из условий прочности ребра на срез: h _р ^тр = N_p /2* t_p * R_s = 57200/2*1,0*1360 = 21,1 см

Принимаем h _р = 22см >h_р ^тр = 21,1см. Во избежании выпучивания h_р / t_p = 22,0/1,0 = 22<30,

l _р / t_p = h_к / t_p = 36/1,0 = 36 < 50.

Принятая конструкция базы

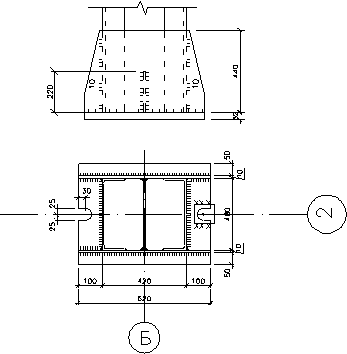
7.5 Расчет оголовка

Конструктивно принимаем t’ _пл = 2,0 см и K_f = 1,0 см.

Высота диафрагмы из условия прочности сварных швов

h _д ^тр = N / (4 * β_f * K_f * R_wf * γ_c * γ_wf ) + 1,0 = 232*10³ /(4*0,7*1,0*1850*1*1,0) + 1,0 = 44 см

Принимаем h _д = 44 см

Требуемая толщина диафрагмы из условия прочности торца на смятие

t _д.см ^тр = N / ((b_f ‘ + 2 * t_пл ‘ ) * R_p ) = 232*10³ / ((25 +2*2,0)*3510) = 2,4 см

Требуемая толщина диафрагмы из условия прочности на срез

t _д.ср ^тр = N / (2 * h_д * R_S ) = 232*10³ / ((2*50*1360) = 1,96 см

Принимаем t _д = 2,4 см > t_д.ср ^тр = 1,96 см

Толщина планок, к которым крепится диафрагма

t _пл ≥ 0,5 t_д = 0,5*2,4 = 12 мм

Принимаем t _пл = 1,2 см.

Принятая конструкция оголовка

Список литературы

[Электронный ресурс]//URL: https://drprom.ru/referat/rabochaya-ploschadka-promyishlennogo-zdaniya/

1. СНиП П-23-81. Стальные конструкции. Нормы проектирования. М.: Стройиздат, 1982. 96 с.

2. СНиП П-6-74. Нагрузки воздействия. Госстой СССР. М.: Стройиздат, 1976. 54 с.

3. Металлические конструкции: Учебник для вузов / Под ред. Е.И. Беленя. – 6-е изд., перераб./ М.: Стройиздат, 1985. 560стр.

4. Михайлов А.М. Сварные конструкции. И., Стройиздат, 1983. 367 с.

5. Лапшин Б.С. К расчету балок в упругопластической стадии по СНиП П-23-81. – В кн.: Металлические конструкции и испытания сооружений: межвуз. темат. сб. тр. Л.: ЛИСИ, 1984, с. 68-75.