Термодинамика – раздел физики, изучающий соотношения и превращения теплоты и других форм энергии. В отдельные дисциплины выделились химическая термодинамика, изучающая физико-химические превращения, связанные с выделением или поглощением тепла, а также теплотехника.
В термодинамике имеют дело не с отдельными молекулами, а с макроскопическими телами, состоящими из огромного числа частиц. Эти тела называются термодинамическими системами. В термодинамике тепловые явления описываются макроскопическими величинами – давление, температура, объём, которые не применимы к отдельным молекулам и атомам.
Термодинамические
Термодинамические циклы являются моделями процессов, происходящих в реальных тепловых машинах для превращения тепла в механическую работу, а также для отъема тепла от более холодного тела и передачи его более горячему (охлаждения) под действием механической работы.
Компонентами любой тепловой машины являются рабочее тело, нагреватель и холодильник (с помощью которых меняется состояние рабочего тела), термодинамический КПД водяной пар газ.
Обратимым называют цикл, который можно провести как в прямом, так и в обратном направлении в замкнутой системе. Суммарная энтропия системы при прохождении такого цикла не меняется. Единственным обратимым циклом для машины, в которой передача тепла осуществляется только между рабочим телом, нагревателем и холодильником, является Цикл Карно.
Цель работы д
-
Изохорный, изобарный, изотермный, адиабатный, политропный процессы
Среди равновесных процессов, происходящих с термодинамическими системами, выделяются изопроцессы, при которых один из основных параметров состояния сохраняется постоянным.
Изохорный процесс (V = const).
График зависимости между параметрами состояния идеального газа при V = const называется изохорой. Изохора в координатах р, V изображается прямой, параллельной оси ординат (рис. 1), где процесс 1 – 2 есть изохорное нагревание, а 3 – 4 – изохорное охлаждение. При изохорном процессе газ не совершает работы над внешними телами, т. е.
Совершенствование процесса гидроочистки
... количество тепла дает реакция сатурации олефинов. Термодинамика процесса Термодинамически процесс гидроочистки ... современным требованиям необходимо совершенствование процесса гидроочистки. 1. АНАЛИТИЧЕСКИЙ ОБЗОР ... тепло. Сера может встречаться в различных формах во всем диапазоне перегонки сырья. Более легкие соединения, такие как меркаптаны и дисульфиды легко превращаются в H2S. Превращение ...
Из первого начала термодинамики (Q = dU + ЬА) для изохорного процесса следует, что вся теплота, сообщаемая газу, идет на увеличение его внутренней энергии:
Согласно формуле ,
Тогда для произвольной массы газа получим
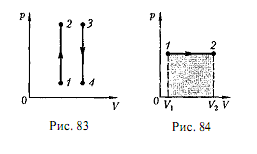
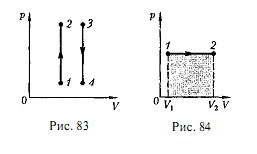
Рис. 1 Рис. 2
Изобарный процесс (р = const).
График зависимости между параметрами состояния идеального газа при р = const называется изобарой. Изобара в координатах р, V изображается прямой, параллельной оси V. При изобарном процессе работа газа при увеличении объема от V1 до V2 равна и определяется площадью тонированного прямоугольника (рис. 2).
Если использовать уравнение Клапейрона – Менделеева для выбранных нами двух состояний, то , откуда .
Тогда выражение для работы изобарного расширения примет вид .
Из этого выражения вытекает физический смысл молярной газовой постоянной R: если
В изобарном процессе при сообщении газу массой
При этом газ совершит работу, определяемую выражением (54.3).
Изотермический процесс (Т = const).
Изотермический процесс описывается законом Бойля – Мариотта: pV= const.
График зависимости между параметрами состояния идеального газа при Т = const называется изотермой. Изотерма в координатах р, V представляет собой гиперболу (рис. 3), расположенную на диаграмме тем выше, чем выше температура, при которой происходит процесс.
Рис. 3
Исходя из выражений (52.2) и , найдем работу изотермического расширения газа:
Так как при Т = const внутренняя энергия идеального газа не изменяется:
то из первого начала термодинамики следует, что для изотермического процесса т.е. все количество теплоты, сообщаемое газу, расходуется на совершение им работы против внешних сил:
Следовательно, для того чтобы при расширении газа температура не понижалась, к газу в течение изотермического процесса необходимо подводить количество теплоты, эквивалентное внешней работе расширения.
Адиабатным называется процесс, при котором отсутствует теплообмен между системой и окружающей средой (Q = 0).
К адиабатным процессам можно отнести все быстропротекающие процессы. Адиабатным процессом, например, можно считать процесс распространения звука в среде, так как скорость распространения звуковой волны настолько велика, что обмен энергией между волной и средой произойти не успевает. Адиабатные процессы применяются в двигателях внутреннего сгорания (расширение и сжатие горючей смеси в цилиндрах), в холодильных установках и т.д. Из первого начала термодинамики для адиабатного процесса следует, что т. е. внешняя работа совершается за счет изменения внутренней энергии системы.
Механика жидкостей и газов в законах и уравнениях
... давления вдоль трубки -- в местах, где скорость больше, давление должно быть меньше, и наоборот. Аналитическую связь между скоростью течения и давлением мы уста-новим в следующем параграфе. 2. Уравнение Бернулли В реальных жидкостях ... t объем жидкости, равный SvДt , а в единицу времени объем (39.1) Жидкость, плотность которой всюду одинакова и изменяться не может, называется несжимаемой. На рис. 39.3 ...
Используя выражения и , для произвольной массы газа перепишем уравнение в виде .
Продифференцировав уравнение состояния для идеального газа , получим
Исключим из и температуру Т:
Разделив переменные и учитывая, что , найдем
Интегрируя это уравнение в пределах от р1 до р2 и соответственно от V1 до V2, а затем потенцируя, придем к выражению
или .
Так как состояния 1 и 2 выбраны произвольно, то можно записать
Полученное выражение есть уравнение адиабатного процесса, называемое также уравнением Пуассона.
Для перехода к переменным Т, V или р, Т исключим из с помощью
уравнения Клапейрона – Менделеева соответственно давление или объем:
Выражения , , представляют собой уравнения адиабатного процесса. В этих уравнениях безразмерная величина
называется показателем адиабаты (или коэффициентом Пуассона).
Для одноатомных газов, достаточно хорошо удовлетворяющих условию идеальности, r = 3, = 1,67. Для двухатомных газов i = 5, = 1,4. Значения , вычисленные по формуле
, хорошо подтверждаются экспериментом.
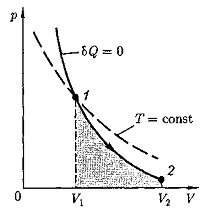
Рис. 4
График зависимости между параметрами состояния идеального газа при δQ =.0 называется адиабатой. Адиабата в координатах р, V изображается гиперболой (рис. 4).
На рисунке видно, что адиабата () более крута, чем изотерма (pV = const).
Это объясняется тем, что при адиабатном сжатии увеличение давления газа обусловлено не только уменьшением его объема, как при изотермическом сжатии, но и повышением температуры.
Вычислим работу, совершаемую газом в адиабатном процессе. Запишем уравнение в виде
Если газ адиабатно расширяется от объема V1 до V2, то его температура уменьшается от Т1 до
Основные термодинамические процессы идеального газа
... работу: где F — сила, с которой газ действует на поршень. Перепишем уравнение: итого работа будет равна [7] [8] : где — давление газа, ... при изобарном процессе в идеальном газе Работа, совершаемая газом при расширении или сжатии газа, равна A = PΔV. ... изотермического процесса в идеальном газе записывается в виде: 5. Адиабатный процесс Основное уравнение термодинамики для адиабатического процесса ...
Применяя те же приемы, что и при выводе формулы , выражение для работы при адиабатном расширении можно преобразовать к виду
где
Работа, совершаемая газом при адиабатном расширении 1 – 2 (определяется тонированной площадью на рис. 4), меньше, чем при изотермическом расширении. Это объясняется тем, что при адиабатном расширении происходит охлаждение газа, тогда как при изотермическом температура поддерживается постоянной за счет притока извне эквивалентного количества теплоты.
Рассмотренные изохорный, изобарный, изотермический и адиабатный процессы имеют общую особенность – они происходят при постоянной теплоемкости. В первых двух процессах теплоемкости соответственно равны и Ср, в изотермическом процессе (dT = 0) теплоемкость равна ±оо, в адиабатном (Q = 0) теплоемкость равна нулю. Процесс, в котором теплоемкость остается постоянной, называется политропным.
Исходя из первого начала термодинамики при условии постоянства теплоемкости (С = const), можно вывести уравнение политропы: где п – – показатель политропы. График зависимости между параметрами состояния идеального газа при С = const называется политропой. Политропа в координатах р, V – гипербола, занимающая промежуточное положение между изотермой и адиабатой.
Очевидно, что при С = 0, п – из получается уравнение адиабаты; при С = оо, п – 1 – уравнение изотермы; при С = Ср, п – 0 – уравнение изобары, при С = Су, п = ±оо – уравнение изохоры. Таким образом, все рассмотренные процессы являются частными случаями политропного процесса.[4]
-
Процессы сжатия в компрессоре
Понятие компрессорные машины охватывает все возможные типы машин, предназначенных для сжатия газов и паров. По принципу действия компрессоры можно разбить на три основные группы: объемные, динамические и струйные. К объемным компрессорам относятся поршневые, ротационные и винтовые. К лопаточным компрессорам относятся центробежные и осевые. Струйные компрессоры из-за весьма низкого КПД не получили широкого распространения в промышленности.
Основными параметрами, характеризующими работу компрессорных машин, можно считать соотношение давлений сжатия, определяемое как отношение давления рабочего тела за компрессором к давлению рабочего тела перед компрессором, и их подачу. Под подачей принято понимать секундное или часовое количество газа или пара, которое подает компрессор, выраженное в кубических метрах газа или пара при параметрах, которые они имеют на входе в компрессор.
Поршневой одноступенчатый компрессор состоит из цилиндра (1); поршня (2), совершающего возвратно–поступательное движение, двух клапанов (3) – всасывающего и нагнетательного (рис. 5).
Компрессор работает следующим образом. При движении поршня слева направо давление газа в цилиндре становится меньше давления во всасывающем патрубке. Всасывающий клапан открывается и по мере движения поршня в крайнее положение полость цилиндра заполняется газом теоретически по линии n – 1 . При обратном движении поршня справа налево всасывающий клапан закрывается и поршень сжимает газ в цилиндре теоретически по кривой 1 – 2 , пока давление в цилиндре не достигает давления р 2 , равного давлению газа в нагнетательной линии трубопровода. Открывается нагнетательный клапан и поршень выталкивает газ в нагнетательную линию трубопровода при постоянном давлении р 2 (линия 2 – 3).
Электропривод компрессора
... компрессорного агрегата, ; А - работа сжатия 1 воздуха до рабочего давления, Дж/; индикаторный политропический КПД компрессора, ... показатели в процессе эксплуатации. При установке электродвигателя с ... 1.3 Задача проектирования электропривода Совокупность определённым ... газ в специальные емкости , которые способны выдержать то давление которое может создать компрессор. Компрессор очень важная установка ...
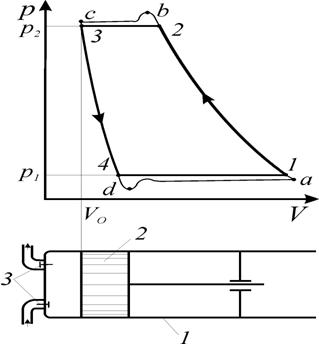
Рис. 5. Принципиальная схема одноступенчатого поршневого компрессора и индикаторная диаграмма
В начале нового хода поршня слева направо, вновь открывается всасывающий клапан, давление в цилиндре падает с р 2 до р 1 теоретически мгновенно (линия 3 – n )и процесс повторяется.
Площадь
Процессы, протекающие в реальных компрессорах, достаточно сложны, так как при этом приходится учитывать влияние вредного пространства, обусловленного тем, что поршень не может доходить в левом крайнем положении вплотную до крышки цилиндра и поэтому между поршнем и крышкой цилиндра всегда остается некоторый объем. В реальных компрессорах приходится учитывать потери давления при течении газа через клапаны, трение поршня о стенки цилиндра, утечки газа через неплотности и т. д. Все это вместе взятое сильно изменяет вид индикаторной диаграммы поршневого компрессора. В частности, из-за наличия сжатого газа во вредном пространстве при движении поршня слева направо, давление газа в цилиндре изменяется по линии 3–4 , а не мгновенно по линии 3–n . Всасывающий клапан открывается не при давлении р 1 , а при давлении, которому соответствует точка d .
То же самое относится к работе нагнетательного клапана, который открывается при давлении несколько большем, чем давление р 2 .
Анализируя работу компрессора по индикаторной диаграмме, нельзя говорить, как это иногда делается, о круговом процессе (или цикле) компрессора, потому что в компрессоре осуществляется только один процесс сжатия по линии 1–2 (или по линии а–b в реальном компрессоре).
Химические процессы и явления при эксплуатации холодильных машин и аппаратов
... естественной конвекцией. Перемещение газов при естественной конвекции происходит с небольшой скоростью. Поэтому в холодильной технике часто применяется принудительная ... холодильной техники и возможность использования огромных количеств холода. Искусственное охлаждение входит как необходимое звено в большое количество процессов химической технологии. С помощью холода сжижают и разделяют газы, ...
Во время процессов всасывания (линия 4–1 ) и нагнетания (линия 2–3 ) состояние газа теоретически не меняется.
При анализе термодинамического процесса сжатия газа в компрессоре основной интерес обычно представляет определение работы, затрачиваемой на сжатие газа, и конечной температуры процесса сжатия.
Удельную работу процесса сжатия можно найти из уравнения первого начала термодинамики, записанного для потока. При этом полагают, что процесс сжатия в компрессоре происходит при следующих условиях: теплообмен с окружающей средой весьма мал и, следовательно, ; скорости движения газа во всасывающем и нагнетательном патрубках равны с 1 = с 2 ; изменением высоты центра тяжести потока можно пренебречь z 1 =z 2 ; необратимые потери работы отсутствуют ().
При этих условиях уравнение упрощается и удельная работа, затрачиваемая на сжатие 1 кг газа или пара в компрессоре, будет определяться соотношением
Для идеального газа это выражение принимает вид где
Величина
Из соотношения видно, что удельная работа сжатия по абсолютной величине равна увеличению энтальпии сжимаемого газа или пара .
Если обозначить расход газа через компрессор (
Полученные уравнения справедливы как для поршневых, так и для лопаточных машин, поэтому процессы сжатия газа в поршневых или лопаточных машинах с термодинамической точки зрения идентичны. Уравнения справедливы для всех реальных газов, а также для определения работы и мощности, затрачиваемых в насосах при перекачке жидкостей.
Для обратимого адиабатного процесса удельная работа сжатия идеального газа определяется из соотношения
Работа сжатия газа в реальном процессе определяется после введения понятия внутреннего относительного КПД компрессора η ic ,характеризующего необратимые потери при сжатии .
Из диаграмм (рис. 6) видно, что в реальном компрессоре из-за необратимых потерь линия процесса сжатия идет правее линии обратимого процесса. Это связано с тем, что необратимые потери работы переходят в теплоту внутреннего теплообмена и энтропия при этом возрастает.
Отношение потенциальных работ и в процессах сжатия
На диаграмме (рис. 7) видно, что переход от адиабатного процесса сжатия (
Рис. 6. Процесс сжатия в компрессоре в диаграмме h – s
Циклы теплового двигателя
... реферате предстоит решить следующие задачи: изучить понятие и общие положения о тепловых двигателях; рассмотреть коэффициент полезного действия теплового двигателя; рассмотреть принцип работы Цикла Карно и его КПД. ... процесс на диаграмме ( p , V ). abc – кривая расширения, cda – кривая сжатия. Работа A в круговом процессе ... охладителю). В поршневых тепловых двигателях горячий газ расширяется в цилиндре, ...
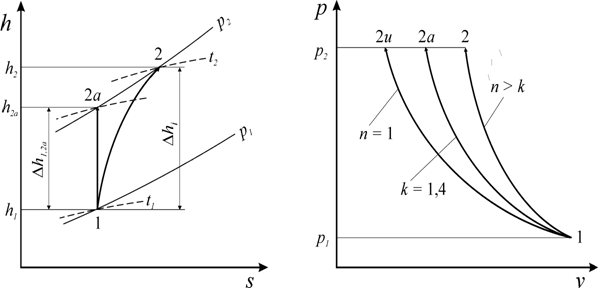
Рис. 7. Процесс сжатия в компрессоре при различных показателях процесса
Для изотермического процесса удельная работа обратимого сжатия идеального газа может быть определена по уравнению
Таким образом, реализация изотермического процесса в компрессорах, при проведении которого необходимо постоянно отводить теплоту, чтобы температура газа в процессе оставалась неизменной, практически трудно осуществима. Изотермический процесс сжатия является как бы эталонным, к которому стремятся приблизить реальный процесс сжатия газа в компрессорах.[1]
-
Цикл Карно
Основываясь на втором начале термодинамики, Карно вывел теорему, носящую теперь его имя:
Из всех периодически действующих тепловых машин, имеющих одинаковые температуры нагревателей и холодильников, наибольшим КПД обладают обратимые машины. Причем КПД обратимых машин, работающих при одинаковых температурах нагревателей и холодильников, равны друг другу и не зависят от конструкции машины и от природы рабочего вещества. При этом КПД меньше единицы. [2]
Цикл Карно является обратимым циклическим процессом с двумя источниками теплоты, имеющими разные, но постоянные температуры. Так как температуры источников тепла постоянные, а процессы получения и отдачи рабочим веществом тепла должны быть обратимыми, то эти процессы могут быть только изотермическими. При этом температура рабочего вещества в цикле должна, очевидно, меняться без теплообмена с окружающей средой, т.е. в адиабатных условиях. Поэтому цикл Карно состоит из двух обратимых изотермических и двух обратимых адиабатных процессов, чередующихся между собой.
Цикл Карно осуществляется рабочим веществом следующим образом (рис. 8).
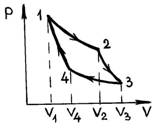
Рис. 8
Рабочее вещество, расширяясь изотермически от состояния 1() до состояния 2(), получает количество тепла от горячего источника, имеющего температуру на бесконечно малую величину dT большую, чем температура рабочего вещества (обратимость), т. е. . При этом, если в качестве рабочего вещества взять идеальный газ, то он производит работу, равную количеству полученного тепла .
В состоянии 2 к рабочему веществу прекращается подвод тепла и затем в обратимом адиабатном процессе расширения до объема температура рабочего вещества уменьшается до температуры T 2 , которая на бесконечно малую величину dT больше температуры холодного источника . Далее рабочее вещество изотермически () обратимо сжимается от объема V 3 до объема V 4 . При этом рабочее вещество (идеальный газ) отдает холодному источнику количество тепла
Термодинамические циклы тепловых и холодильных машин
... определяющие состояние рабочего тела (давление, объём, температура, энтропия), совпадают. Термодинамические циклы являются моделями процессов, происходящих в реальных тепловых машинах для превращения тепла в механическую работу. Компонентами любой тепловой машины ...
Откуда находим
Наконец, замыкающим цикл процессом является обратимый адиабатный процесс, в котором рабочее вещество возвращается в начальное состояние 1.
Вычислим КПД цикла Карно. По определению КПД любого цикла
Подставляя выражения и в , получим
Из последнего выражения видно, что КПД цикла не зависит от количества рабочего вещества
;
Откуда находим
Подставив последнее выражение в , будем иметь:
Таким образом, КПД цикла Карно, произведенного с идеальным газом, определяется только температурами T 1 (горячего) и T 2 (холодного) источников тепла. При этом тем больше, чем больше разность между T 1 и T 2 . КПД цикла Карно равен 1 в двух практически недостижимых случаях: когда T 1 = ∞ или, когда T 2 = 0. Если КПД цикла равен единице, то из выражения следует, что Q 2 = 0, т. е. все тепло Q 1 , полученное от горячего источника, преобразуется в работу, что запрещено вторым началом термодинамики. Следовательно, КПД никакого цикла, в том числе и цикла Карно, не может быть равен единице.[3]
Заключение
Если в термодинамической системе меняется хотя бы один из параметров любого входящего в систему тела, то в системе происходит термодинамический процесс.
Основные термодинамические параметры состояния Р ( давление ), V ( объем ), Т (температура) однородного тела зависят один от другого и взаимно связаны.
Термодинамические процессы часто изображаются на графиках состояния, где по осям отложены параметры состояния. Точки, на плоскости такого графика, соответствуют определенному состоянию системы, линии на графике соответствуют термодинамическим процессам, переводящим систему из одного состояния в другое.
Контрольная работа: Состояние окружающей среды города Сыктывкара
... воздух города Сыктывкара. Перечень веществ, контролируемых всеми службами на стационарных и маршрутных постах г.Сыктывкара. Вещество Среднегодовая концентрация (мг/м3) Среднегодовая концентрация (мг/м3) Общее население территории Общее население территории ... будут приведены в таблицах. Состояние окружающей среды города Сыктывкара Состояние окружающей среды г.Сыктывкара на протяжении последних лет ...
Если поршень зафиксирован, и объем не меняется, то произойдет повышение давления в сосуде. Такой процесс называется изохорным ( V = const ), идущий при постоянном объеме.
Если поршень свободен то нагреваемый газ будет расширятся при постоянном давлении такой процесс называется изобарным ( P = const ), идущим при постоянном давлении.
Если, перемещая поршень, изменять объем газа в сосуде то, температура газа тоже будет изменяться, однако можно охлаждая сосуд при сжатии газа и нагревая при расширении можно достичь того, что температура будет постоянной при изменениях объема и давления, такой процесс называется изотермическим ( Т = const ).
Процесс, при котором отсутствует теплообмен между системой и окружающей средой, называется адиабатным , при этом количество теплоты в системе остается постоянными (Q=const).
Термодинамические процессы, в результате которых рабочее тело, проходя последовательно различные состояния, возвращается снова в первоначальное (исходное) состояние, называются замкнутыми процессами или циклами.
Термодинамические циклы описывают работу идеальных тепловых машин, в которых тепло превращается в механическую работу наиболее совершенно, так как предполагается, что они работают без трения, без охлаждения стенок цилиндра, и не принимаются во внимание многие другие обстоятельства, имеющие место в реальных двигателях и понижающие степень совершенства преобразования в них теплоты в работу. Таким образом, изучение идеальных термодинамических циклов позволяет определить наибольшее возможное с термодинамической точки зрения значение коэффициента полезного действия превращения теплоты в механическую работу в рассматриваемых условиях.
Практическое задание
В баллоне вместимостью 0,1 м
V 1 = 0,1
T
р1 = 5 Па
Т2 = 273К (норм. усл.)
р2 = Па (норм. усл.)
Воспользуемся уравнением Менделеева-Клапейрона:
Выразим из этого уравнения объем :
Выделим объем, подставив известные значения:
= ?
Ответ:
Список литературы
[Электронный ресурс]//URL: https://drprom.ru/referat/rabota-rasshireniya-gaza/
-
Кузнецов В.Н., В. В. Овсянников, А. С. Анисимов, М. В. Кокшаров, В. В. Крайнов; Термодинамика и теплопередача : Учебное пособие. Омский гос. ун-т путей сообщения. Омск, 2006. 128 с.
-
Кузнецов С.И. Термодинамика: учебное пособие / под ред. В.В. Ларионова. Томск: Издательство ТПУ, 2011. 177 с.
-
Савушкин Л.Н. Молекулярная физика и термодинамика: учебное пособие. СПб.: Издательство СПбГУТ, 2012. 58 с.
-
Трофимова Т.И. Курс физики: учеб. пособие для вузов. М.: Издательский центр «Академия», 2006. 560 с.
