Я выбрала эту тему, потому что она была и остается актуальной в наше время.
Сейчас почти в любой отрасли науки и техники встречается применение графов. В физике — при построении электрических схем, в химии и биологии
— при изучении молекул и их цепочек, в географии – при составлении карт, в истории – при составлении родословной,
в геометрии – в чертежах многоугольников, многогранников, пространственных фигур, в экономике – при решении задач о выборе оптимального пути для потоков (схем авиалиний , метро, железных дорог).
Графами являются блок-схемы программ для ЭВМ, сетевые графики строительства. С помощью графов решается задача о назначении на должности. А именно: если имеется несколько вакантных должностей и группы лиц, желающих их занять, причем каждый из претендентов имеет квалификацию для нескольких должностей, то при каких условиях каждый из претендентов сможет получить работу по одной из своих специальностей?
Теория графов в школьной программе не изучается, но широко применяется при решении математических олимпиадных задач.
II. 1. История возникновения теории графов
Изучив информацию Интернет-ресурсов, я для себя открыла следующие интересные факты об истории теории графов.
Родоначальником теории графов принято считать математика Леонарда Эйлера.
Историю возникновения этой теории можно проследить по переписке великого ученого. В ней он сообщал, что ему была предложена задача о семи мостах Кенигсберга. Спрашивалось, может ли кто-нибудь непрерывно обойти их, проходя только однажды через каждый мост. И ему сразу же было сообщено, что никто еще до сих пор не мог это проделать, но никто и не доказал, что это невозможно. Вопрос этот показался ему достойным внимания тем, что «…Для его решения недостаточны ни геометрия, ни алгебра, ни комбинаторное искусство…». После долгих размышлений он нашел легкое правило, основанное на вполне убедительном доказательстве, с помощью которого можно во всех задачах такого рода определить, может ли быть совершен такой обход через какое угодно число и как угодно расположенных мостов или не может. Кенигсбергские же мосты расположены так, что их можно представить на рисунке, на котором А обозначает остров, а В, С и D — части континента, отделенные друг от друга рукавами реки. Семь мостов обозначены буквами а, b, с, d, е, f, g.
Модели на основе теории графов импульсные модели
... понятия теории. §3. ОСНОВНЫЕ ТЕОРЕМЫ ТЕОРИИ ГРАФОВ. Опираясь на приведенные выше определения теории графов, приведем формулировки и доказательства теорем, которые затем найдут свои приложения при решении задач. Теорема ... долгих размышлений я нашел легкое правило, основанное на вполне убедительном доказательстве, с помощью которого можно во всех задачах такого рода тотчас же определить, может ли ...
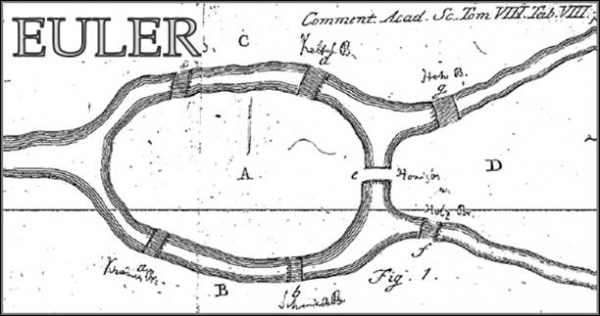
http://www. cba. upc. edu/projects/logos/Euler_logo. png Кенигсбергские мосты.
Математик писал, что переход возможен, если на участке разветвления реки имеется не более двух областей, в которые ведет нечетное число мостов.
Для того чтобы проще представить себе это, будем стирать на рисунке уже пройденные мосты. Легко проверить, что если начать двигаться в соответствии с правилами Эйлера, пересечь один мост и стереть его, то на рисунке будет изображен участок, где опять имеется не более двух областей, в которые ведет нечетное число мостов. А при наличии областей с нечетным числом мостов мы будем располагаться в одной из них. Продолжая двигаться так далее, пройдем через все мосты по одному разу.
История с мостами города Кенигсберга имеет современное продолжение. В некоторых учебниках математики или в дополнительных материалах (приложениях) учебника можно встретить задачи, чьё решение основано именно на предложенном Эйлером способе.
Я поняла, что в ходе рассуждений Эйлер пришёл к следующим выводам:
Число нечётных вершин (вершин, к которым ведёт нечётное число рёбер) графа должно быть чётно. Не может существовать граф, который имел бы нечётное число нечётных вершин. Если все вершины графа чётные, то можно, не отрывая карандаша от бумаги, начертить граф, при этом можно начинать с любой вершины графа и завершить его в той же вершине. Граф с более чем двумя нечётными вершинами невозможно начертить одним росчерком.
Граф кёнигсбергских мостов имел четыре нечётные вершины (т. е. все), следовательно, невозможно пройти по всем мостам, не проходя ни по одному из них дважды.
Я, изучив эти выводы, решила проверить их на примерах других задач из раздела теории графов.
В заключение отмечу, что первая работа о графах принадлежала Л. Эйлеру и появилась в 1736 году. В дальнейшем над графами работали Кениг (), Гамильтон (), из современных математиков – К. Берж, О. Оре, А. Зыков.
2. Некоторые задачи теории графов
Задач по теории графов не так много. Я рассмотрела материалы
Интернет-ресурсов и книг, разобрала предлагаемые там задачи, попыталась их систематизировать и выделила из них разные, на мой взгляд, задачи, решаемые с помощью графов:
2.1 Логические задачи
Задача 1 . Аркадий, Борис. Владимир, Григорий и Дмитрий при встрече обменялись рукопожатиями (каждый пожал руку каждому по одному разу).
Сколько всего рукопожатий было сделано?
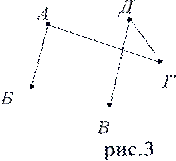
Пусть каждому из пяти молодых людей соответствует определенная точка на плоскости, названная первой буквой его имени (рис.2), а производимому рукопожатию — отрезок или часть кривой, соединяющая конкретные точки — имена (рис. 3).
|
Нулевой граф с пятью вершинами |
Неполный граф с пятью вершинами |
http://school-sector. *****/dckt/projects/ctrana/graf/gr1.htm
Точки А, Б, В, Г, Д называются вершинами графа, а отрезки линий, соединяющие эти точки — ребрами графа. При изображении графов на рисунках или схемах отрезки могут быть прямолинейными или криволинейными; Длины отрезков и расположение точек произвольны.
Рассмотрим процесс соединения точек А, Б, В, Г, Д ребрами.
1. Ситуация, соответствующая моменту, когда рукопожатия еще не совершались, представляет собой точечную схему, изображенную на рисунке 2. Такая схема, состоящая из «изолированных» вершин, называется нулевым графом.
2. Ситуация, когда совершены еще не все рукопожатия, может схематически быть изображена, например, с помощью рисунка З: пожали руки А и Б, А и Г, Д и Г, В и Д.
Графы, в которых не построены все возможные ребра, называются неполными графами.
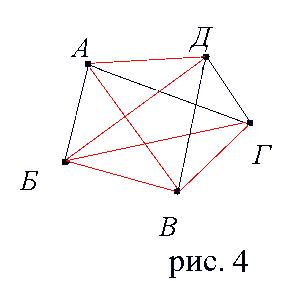
3. На рисунке 4 изображен граф, соответствующий всем совершенным рукопожатиям. Этот граф является полным графом.
|
Полный граф с пятью вершинами |
Если подсчитать число ребер графа, изображенного на рисунке 4, то это число и будет равно количеству совершенных рукопожатий между пятью молодыми людьми. Их 10. |
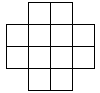
Задача 2 . Доска имеет форму двойного креста, который получается, если из квадрата 4×4 убрать угловые клетки.
http://*****/files/articles/41/4169/416943/img2.gif
Можно ли обойти ее ходом шахматного коня и вернуться на исходную клетку, побывав на всех клетках ровно по одному разу?
Решение: я занумеровала последовательно все клетки:
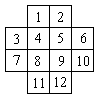http://*****/files/articles/41/4169/416943/img3.gif
А теперь с помощью рисунка показала, что такой обход таблицы, как указано в условии, возможен:
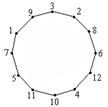http://*****/files/articles/41/4169/416943/img4.gif
Задача 3 . В городе Маленьком 15 телефонов. Можно ли их соединить проводами так, чтобы каждый телефон был соединен ровно с пятью другими?
Решение: я допустила, что такое соединение телефонов возможно. Тогда представляю себе граф, в котором вершины обозначают телефоны, а ребра – провода, их соединяющие. Считаю, сколько всего получится проводов. К каждому телефону подключено ровно 5 проводов, т. е. степень каждой вершины графа – 5. Чтобы найти число проводов, надо просуммировать степени всех вершин графа и полученный результат разделить на 2 (т. к. каждый провод имеет два конца, то при суммировании степеней каждый провод будет взят 2 раза).
Но тогда количество проводов получится разным 
. Но это число не целое. Значит мое предположение о том, что можно соединить каждый телефон ровно с пятью другими, оказалось неверным.
Ответ. Соединить телефоны таким образом невозможно.
При решении этой задачи я выяснила, как подсчитать число ребер графа, зная степени всех его вершин. Для этого нужно просуммировать степени вершин и полученный результат разделить на два.
Задача 4. В государстве 100 городов, из каждого города выходит 4 дороги. Сколько всего дорог в государстве?
Решение. Подсчитаем общее количество выходящих городов дорог – = 400. Однако при таком подсчете каждая дорога посчитана 2 раза – она выходит из одного города и входит в другой. Значит всего дорог в два раза меньше, т. е. 200.
Задача 5 . Может ли в государстве, в котором из каждого города выходит ровно 3 дороги, быть ровно 100 дорог?
Решение. Подсчитаю число городов. Число дорог равно числу городов х, умноженному на 3 (число выходящих из каждого города дорог) и разделенному на 2.Тогда 100 = Зх/2 => Зх=200, чего не может быть при натуральном х. Значит, 100 дорог в таком государстве быть не может.
2.2 Задачи на связность.
Есть еще одно важное понятие, относящееся к графам – понятие связности.
Граф называется связным, если две его любые вершины можно соединить путем, т. е. непрерывной последовательностью ребер.
Существует целый ряд задач, решение которых основано на понятии связности графа.
Графы Эйлера.
Я часто сталкивалась с задачами, в которых требуется нарисовать какую-либо фигуру, не отрывая карандаш от бумаги и проводя каждую линию только один раз. Оказывается, что такая задача не всегда разрешима, т. е. существуют фигуры, которые указанным способом нарисовать нельзя. Вопрос разрешимости таких задач также входит в теорию графов. Впервые его исследовал в 1736 году великий немецкий математик Леонард Эйлер, решая задачу о Кенигсбергских мостах. Поэтому графы, которые можно нарисовать указанным способом, называются Эйлеровыми графами.
Задача 1 . Можно ли нарисовать изображенный на рисунке граф не отрывая карандаш от бумаги и проводя каждое ребро ровно один раз?
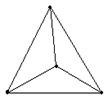http://*****/files/articles/41/4169/416943/img9.gif
Решение. Если я буду рисовать граф так, как сказано в условии, то в каждую вершину, кроме начальной и конечной, я войду столько же раз, сколько выйдем из нее. То есть все вершины графа, кроме двух должны быть четными. В нашем же графе имеется три нечетные вершины, поэтому его нельзя нарисовать указанным в условии способом.
2.3 Задачи по теореме Эйлера о нечетных вершинах
Задача 1 . В классе 30 человек. Может ли быть так, что 9 человек имеют по 3 друга, 11 – по 4 друга, а 10 – по 5 друзей?
Ответ. Нет (по теореме о четности числа нечетных вершин).
Задача 2 . У короля 19 баронов-вассалов. Может ли оказаться так, что у каждого вассального баронства 1, 5 или 9 соседних баронств?
Ответ. Нет, не может. В противном случае получился бы граф соседства баронств с нечетным количеством нечетных вершин.
3. Применение теории графов.
Чем больше я изучала теорию графов, тем больше поражалась разнообразию применения этой теории. Графы применяются в различных отраслях науки.
3.1.Графы и информация
Графы играют весьма важную роль в теории информации. Предположим, что определенное число сообщений требуется закодировать в виде
конечных последовательностей различной длины, состоящих из нулей и единиц. Если вероятности кодовых слов заданы, то наилучшим считается код, в котором средняя длина слов минимальна по сравнению с прочими распределениями вероятности.
3.2.Графы и химия.
Теория графов в химии применяется для решения различных теоретических и прикладных задач. Применение графов теории базируется на построении и анализе различных классов химических и химико-технологических графов, которые называются также топология, т. е. модели, учитывающие только характер связи вершин. Ребра и вершины этих графов отображают химические и химико-технологические понятия, явления, процессы или объекты и соответственно качественные и количественные взаимосвязи либо определенные отношения между ними.
3.3.Графы и биология
Графы играют большую роль в биологической теории ветвящихся процессов. Для простоты я покажу только одну разновидность ветвящихся
процессов – размножение бактерий. Предположим, что через определенный
промежуток времени каждая бактерия либо делится на две новые, либо
погибает. Тогда для потомства одной бактерии я получу двоичное дерево.
Нас будет интересовать лишь один вопрос: в скольких случаях n-е
поколение одной бактерии насчитывает ровно k потомков? Математически вычисляемое на основе значений предыдущих членов последовательности соотношение, обозначающее число необходимых случаев, известно в биологии под названием процесса Гальтона-Ватсона. Его можно рассматривать как частный случай многих общих формул.
3.4.Графы и физика
Еще недавно одной из наиболее сложных и утомительных задач для радиолюбителей было конструирование печатных схем.
Печатной схемой называют пластинку из какого-либо диэлектрика
(изолирующего материала), на которой в виде металлических полосок
вытравлены дорожки. Пересекаться дорожки могут только в определенных точках, куда устанавливаются необходимые элементы, их пересечение в других местах вызовет замыкание электрической цепи.
В ходе решения этой задачи необходимо вычертить плоский граф, с вершинами в указанных точках.
Изучая этот материал, я узнала области применения теории графов и сделала вывод, что этот раздел математики является одним из важнейших, который используется в нашей повседневной жизни часто незаметно для нас.
III. Заключение
Графы – это замечательные математические объекты, с помощью, которых можно решать математические, экономические и логические задачи. Также можно решать различные головоломки и упрощать условия задач по физике, химии, электронике, автоматике. Сама теория графов является частью как топологии, так и комбинаторики.
Таким образом, я сделала вывод, что изучение теории графов актуально для всестороннего развития школьника.
IV. Список литературы и Интернет-ресурсов.
1. «Соросовский образовательный журнал» №11 1996 (ст. «Плоские графы»);
2. «Необычные задачи математики», Киев, «Радяньска школа»
1987(часть 2);
3. «Математические досуги», М. «Мир», 1972(глава 35);
4. «В помощь учителю математики», Йошкар-Ола, 1972 (ст. «Изучение элементов теории графов»);
5. , , «Старинные занимательные
задачи», М. «Наука», 1988(часть 2, раздел 8; приложение 4);
6. «Математические головоломки и развлечения», М. «Мир», 1971;
7. «Графы и их применения», М. «Мир», 1965;
8. «Теория конечных графов», Новосибирск, «Наука», 1969;
9. «Теория графов и ее применение», М., ИЛ, 1962;
10. «Трилогия о математике», М., «Мир», 1980.
11. http://ru. wikipedia. org
12. http://www. *****
13. http://www. *****
14. http://lib. repetitors. eu
