Методика формирования представлений о длине в начальных классах

метки: Отрезка, Измерение, Длина, Единица, Величина, Ребенок, Учащаяся, Учитель

школьник измерение начальный длина

В настоящее время проблемам преподавания математики в школе стали уделять больше внимания. Это связано с научно-техническим прогрессом и развитием наукоемких производств. Технические науки, среди которых, в последнее время, быстро развиваются и имеют огромное практическое значение, такие как информационные технологии, электроника и т.д., немыслимы без математического аппарата.

Основа для математической грамотности закладывается именно в школе, поэтому изучению вопросов, связанных с этим процессом, уделяется пристальное внимание. Математика является одним из опорных предметов школы. Она обеспечивает изучение других дисциплин. Требует от учащихся волевых и умственных усилий, развитого воображения, концентрации внимания, математика развивает личность учащегося. Кроме того, изучение математики существенно способствует развитию логического мышления и расширяет кругозор школьников.

Начальный курс математики — курс интегрированный: в нем объединены арифметический, алгебраический и геометрический материал. При этом основу начального курса составляют представления о натуральном числе и нуле, о четырех арифметических действиях с целыми неотрицательными числами и важнейших их свойствах, а также основанное на этих знаниях осознанное и прочное усвоение приемов устных и письменных вычислений.

Наряду с этим важное место в курсе занимает ознакомление с величинами и их измерением. Важнейшее место в этой работе отводится формированию умений и навыков, связанных с измерением ряда величин, практическому ознакомлению детей с соответствующими измерительными приборами и их шкалами, ознакомлению с системой единиц измерения и с переходом от одной единицы измерения к другим (таблица мер).

В основе методики изучения величин лежит практическая деятельность учащихся, связанная с овладением навыками измерения таких величин, как длина отрезка, площадь фигуры, масса тела, времени.

Большое значение при ознакомлении с величиной имеет использование знаний, умений и навыков, приобретаемых учащимися в связи с изучением фигур и операций над фигурами (деление фигур на части, составление фигур из других).

И наоборот, использование представлений о величине, ее свойствах и измерении в процессе формирования понятия «фигура».

Так, например, на основе представлений о длине дети знакомятся с понятием о длине, единицах ее измерения, учатся измерять длины и расстояния, переводить из одной единицы измерения в другую, выполнять арифметические действия над величинами.

Измерения геометрических величин в курсе геометрии 7-9 классов

... помощь в изучении остальных тем геометрии и достижении целей обучения математике в школе. Без знания разнообразных измерительных инструментов, геометрических величин и без умения производить измерения этих величин обучение геометрии становится невозможным. А в связи ...

Цель исследования:

Задачи исследования данной темы:

1. Изучение литературы (психолого-дидактический, методический и др.) с целью выяснения содержания математических понятий по данной теме.

• проанализировать учебники математики и программы начальной школы с целью изучения вопроса о месте величины длины в их содержании;
• провести экспериментальное исследование для выявления путей и способов формирования знаний о длине.
• Провести самостоятельную или практическую в опытном классе, позволяющую определить уровень сформированности представлений о длине;
• выявить влияние использования системы упражнений на качество знаний и умений учащихся.

Объект исследования:, Предмет исследования:, Гипотеза исследования:

• теоретически обосновать значение и необходимость изучения длины;
• использовать возможности как классно-урочной, так и внеклассной работы для формирования знаний о длине.

Методы исследования:

• изучение и анализ литературы по рассматриваемой проблеме;
• практическая работа, включающая в себя проведение проверочных работ по выявлению уровня сформированности понятия о длине;
• анализ практической деятельности учащихся.

База исследования:

Перейдем к рассмотрению данной темы более подробно.

1. Методические особенности изучения длины и единиц ее измерения на уроках математики в начальной школе

1 Общая характеристика методики изучения величин младшими школьниками

Величина, так же как и число, является основным понятием курса математики начальных классов, в задачу которого входит формирование у детей представления о величине как о некотором свойстве предметов и явлений, которое прежде всего связано с измерением.

В 1-3 классах учащиеся получают представление о таких величинах, как длина, масса, емкость, время, площадь, и о единицах ее измерения. В процессе решения задач они знакомятся с ценой, количеством, стоимостью, скоростью, расстоянием, производительностью и т.д.[2].

По программе курса математики начальных классов предусматривается знакомство с такими величинам и единицами их измерения, как количество, длина, масса, емкость, время, площадь, скорость, стоимость. При изучении каждой величины имеются свои методические особенности, связанные со спецификой данной величины, но общий подход к величине как к свойству предметов и явлений позволяет говорить об общей методике изучения величин. Знание же единого методического подхода позволит учителю осознанно и целенаправленно организовать деятельность учащихся.

Общеметодический подход к ознакомлению с величинами учащихся начальных классов является естественным продолжением методики ознакомления с величинами детей в дошкольных учреждениях. Однако, учитывая то, что некоторые дети не посещали дошкольные учреждения, необходимо обращать внимание на те моменты, которых они могут не знать.

Традиционно, в методике преподавания математики в начальных классах выделяются общие для процесса введения понятия величины следующие этапы[7].

• Задается некоторое множество А, которое является областью определения величины.
• Из данного рода величин выбирается некоторая величина (е), которую называют единицей измерения.
• Осуществляется процесс измерения — сравнения данной величины с выбранной единицей измерения, результатом которого является некоторое значение величины.

Изучение величин в курсе математики начальной школы имеет прикладной характер. Учащиеся знакомятся с непосредственным измерением длин отрезков, определяют вместимость сосудов, массу тел, температуру воздуха, учатся определять время по часам, даты по календарю, площадь фигуры с помощью палетки.

Измерения в маркетинговых исследованиях

... шкалы, измеряемого с помощью определенной единицы измерений, то есть используется количественная информация. ... для измерений определяется характером отношений между объектами, наличием информации и целями исследования. Если, ... говорят, что объект был измерен по данной характеристике. Легче измеряются объективные свойства ... покупки определенного товара (раз в неделю, раз в месяц или чаще). Однако такая ...

В процессе изучения темы важно добиться, чтобы учащиеся научились четко дифференцировать такие тесно связанные между собой, но разные по своей сути понятия, как «величина» и «число». Хотя формирование представлений о той или иной конкретной величине и о способах ее измерения имеет свои особенности, тем не менее, целесообразно выделить общие этапы, которые имеют место при изучении каждой из величин[8]:

1. Выяснение и уточнение имеющихся у детей представлений о данной величине (обращение к опыту ребенка).

2. Сравнение однородных величин (визуально, с помощью ощущений, наложением, приложением, путем использования различных мерок).

• Знакомство с единицей измерения данной величины и с измерительным прибором.
• Формирование измерительных умений и навыков.
• Сложение и вычитание однородных величин, выраженных в единицах одного наименования.

— Знакомство с новыми единицами величины, перевод однородных величин, выраженных в единицах одних наименований, в другие, перевод величин, выраженных в единицах одного наименования, в величины, выраженные в единицах двух наименований, и наоборот.

• Сложение и вычитание величин, выраженных в единицах двух наименований.
• Умножение и деление величины на число.

Ученики, оканчивающие начальную школу, должны знать, что на множестве изученных величин (длина, площадь, вместимость, масса, время) определены отношения равенства и неравенства. Эти отношения можно устанавливать как практически (непосредственно), так и косвенно. Все величины можно измерять, причем для каждой из них есть свой способ измерения, сущность которого заключается в сравнении данного объекта с единицей его измерения. Величины одного и того же рода можно складывать и вычитать; умножать и делить на отвлеченные числа; находить часть величины. Между величинами одного и того же рода существует определенная зависимость, знание которой необходимо для выполнения преобразований величин: выражения одной и той же величины в различных единицах измерения[2].

Обучение измерению разных величин строится по одной и той же схеме.

• Производится сравнение величин «на глаз», с помощью мускульных усилий.
• Вводятся единицы измерения величины и устанавливаются отношения между ними и ранее рассмотренными.
• Величины преобразуются: крупные заменяются мелкими, а мелкие — крупными.
• Величины сравниваются путем измерения.
• Производятся операции над величинами.

Итак, выделяются следующие основные этапы в работе над величинами[13]:

ПЕРВЫЙ ЭТАП. Формирование общего представления о данной величине, в основе которого лежит обращение к опыту ребенка и уточнение имеющихся у него представлений. Введение понятия (на интуитивном уровне) данной величины и соответствующей терминологии.

Применение динамических характеристик средств измерения при измерении ...

... измеряемой величины. Так при одинаковой абсолютной погрешности двух измеренных линий точнее измерена та, длина которой больше. погрешность измерение систематическая случайная 2. Динамические характеристики средств измерений Полные динамические характеристики, Полная динамическая характеристика ...

ВТОРОЙ ЭТАП. Сравнение однородных величин:

• а) визуально (на «глаз»);
• б) с помощью ощущений (ощупывание, «взвешивание» на руках);
• в) наложением, приложением;
• г) с помощью различных мерок.

ТРЕТИЙ ЭТАП. Знакомство с единицей измерения величины и с измерительным прибором. Формирование измерительных умений и навыков.

ЧЕТВЕРТЫЙ ЭТАП. Сложение и вычитание величин, выраженных в единицах одного наименования.

ПЯТЫЙ ЭТАП. Знакомство с новыми единицами измерения величин в тесной связи с изучением нумерации по концентрам. Сложение и вычитание однородных величин, выраженных в одинаковых единицах.

ШЕСТОЙ ЭТАП. Перевод величин, выраженных в единицах одних наименований, в однородные величины, выраженные в единицах других наименований

СЕДЬМОЙ ЭТАП. Сложение и вычитание однородных величин, выраженных в единицах различных наименований.

ВОСЬМОЙ ЭТАП. Умножение и деление величины на число. Деление однородных величин.

С целью формирования представлений о разного рода величинах проводятся практические работы, используются упражнения, применяются демонстрационные и индивидуальные наглядные средства, при этом варьируются коллективные, индивидуальные и групповые формы работы на уроке.

Значение с величинами единицами их измерения имеет не только практическое значение: оно предоставляет большие возможности для формирования умения видеть проблему и находить пути ее решения, тем самым способствуя развитию познавательных способностей учащихся.

2 Общая характеристика методики изучения длины младшими школьниками

школьник измерение начальный длина

Знание мер длины, умение находить длину, ширину, высоту и т.п. необходимы учащимся и в быту, и при овладении профессией. Со всеми мерами длины и их соотношениями учащиеся начальной школы знакомятся в течение всего времени обучения в младших классах, закрепление же этих мер проходит в течение всех лет обучения в школе.

План изучения темы и время введения

1 класс

• Понятие длины как свойства предметов. Прямая и кривая линии.
• Отрезок. Сравнение отрезков.
• Сантиметр.
• Дециметр.
• Метр.

2 класс

• Миллиметр, километр.

3 класс

• Упорядочивание представлений о длине и единицах ее измерения.

Задачи изучения темы

• Сформировать понятие длины как свойства предметов.
• Познакомить с единицами длины и соотношениями между ними.
• Сформировать умения измерять длину данных отрезков и чертить отрезки заданной длины, сравнивать длины.
• Научить выражать величины в меньших и больших единицах.
• Научить выполнять действия над величинами устно и в столбик.

Предварительно отметим, что измерение длин различными мерками предусмотрено программой детского сада, поэтому многие дети уже знакомы с измерением отрезков различными мерками[2].

Подготовительной работой к введению понятия длины отрезка должны быть упражнения следующего характера. Учитель с первых уроков уточняет отношения длиннее — короче, шире — уже, дальше — ближе. Именно этому помогают упражнения на сравнения предметов по длине (кто выше? что толще? что длиннее?).

Величина и её измерение

... величин через сумму: разностью величин а и b называется такая величина с, что а=b+c. Например, если а - длина отрезка АС, b - длина отрезка AB, то длина отрезка ВС есть разность длин отрезков ... единицах разных наименований. Таким образом, чтобы улучшить математическую подготовку детей по теме «Величины и их измерение», необходимо пополнить её новыми упражнениями из системы развивающего обучения. ...

Важным шагом в формировании понятия длины является знакомство с прямой линией и отрезком как «носителями» линейной протяженности. Сравнивая отрезки «на глаз», дети получают представления о равных и неравных отрезках.

При введении (или обобщении) понятия «длина» внимание учащихся необходимо сосредоточить на самом термине «длина», разъяснив соответствующим образом его значение. Так, при проведении беседы можно предложить учащимся сравнить длину карандаша и ручки, которые лежат у них на партах. При сравнении используется прием приложения. Затем можно предложить сравнить по картинке длину ручки и кисточки (ручка короче, кисточка длиннее), сравнить длину красного карандаша и ручки (красный карандаш короче, ручка длиннее).

В данной ситуации дети используют сравнение длин предметов «на глаз», т.к. изображения нельзя сравнить ни наложением, ни приложением. Далее представления учащихся уточняются: нарисованные предметы обладают свойством, которое называется длина. Данные предметы можно сравнивать по длине. Отрезки тоже можно сравнивать по длине. На рисунке должно быть хорошо видно, длина какого отрезка больше, а какого меньше. Эти способы сравнения («на глаз», наложением и приложением) можно назвать неопосредованными способами сравнения.

При использовании мерок (посредников) мы будем применять опосредованные способы сравнения.

Для знакомства с другими способами сравнения длин отрезков рекомендуется организовать практическую работу. Используя полоски из различных материалов, различных цветов, различной длины как модели отрезков, учащиеся сравнивают длины отрезков с помощью различных мерок. Меркой могут выступать узкие полоски бумаги, палочки разной длины и т.д.

При использовании различных мерок для измерения одного отрезка учащиеся получают различные числовые результаты. В процессе выполнения различных практических упражнений они должны осознать зависимость числового результата от величины той мерки, с помощью которой измерялся данный отрезок.

На уроке это можно легко проверить, рассмотрев следующую ситуацию (предложена Истоминой Н.Б.) [9].

На доске начерчен отрезок. Трое детей по очереди измеряют его полосками разной длины. Коля — красной полоской, Миша — зеленой и Дима — белой. В результате измерения Коля получил 6, Миша 3, Дима 1. Кто из них оказался прав? Учащиеся заметили, что каждый мальчик был бы прав, если бы указал в ответе единицу измерения: 6 кр., 3 зел., 1 бел.

Эту же работу можно провести по индивидуальным карточкам, на которых начерчен один и тот же отрезок. Например, отрезок 4 см. Учитель просит учащихся измерить его. Одни учащиеся измеряют данный отрезок одной клеточкой, другие двумя, а третьи за единицу измерения выбрали 4 клетки. Результат измерения получился разный. На доске делается такая условная запись:

После проведения такого рода практических работ у ребят возникает проблема, как же договориться, как измерять длины, чтобы при измерении равных отрезков у всех были одинаковые результаты? Делается вывод, что необходима единая единица длины.

Такой единицей измерения является сантиметр. Учитель демонстрирует модель сантиметра в виде узкой бумажной полоски, части спички, кусочка цветной проволоки длиной 1 см. Сантиметр сравнивается с шириной пальца, с длиной двух клеточек тетради.

Измерение длины линий в геодезии

... длине ленты равно 200м. Число таких передач записывают в журнал измерений. Сюда же записывают результаты измерения неполного пролета: от последней шпильки в полном пролете до конечной точки линии. Для контроля линию ... заросшая местность, снег и т. д.). Измерения линий рулеткой производят аналогично. Однако фиксация концов измеренных отрезков при работе рулеткой должна выполняться более точно ...

Затем знакомит учащихся с линейкой, с правилами пользования данным инструментом для измерения длин отрезков. На парте у каждого ученика должна быть модель сантиметра, изготовленная учителем заранее. Далее эти задачи решаются при помощи масштабной линейки. Ее могут разметить и сами дети (это интересно).

При откладывании отрезков данной длины по линейке на первом этапе ученик должен сначала «прошагать» этот отрезок по сантиметрам, только потом приступать к черчению.

Итак, первой единицей измерения отрезков (при изучении чисел от 1 до 10) является 1 см. Учитель предлагает начертить дома еще один отрезок длиной 1 см и изготовить его модель из цветной бумаги или проволоки. При помощи модели ученики должны уметь решить следующие задачи[16]:

• Измерить заданный отрезок. При этом ученик должен: а) точно приложить конец модели сантиметра к одному из концов отрезка;
• б) с помощью карандаша на отрезке отметить другой конец модели сантиметра;
• в) от этого конца продолжить откладывать мерку до тех пор, пока не последняя отметка не совпадет со вторым концом отрезка;
• г) пересчитав количество вложенных в отрезок моделей, сделать вывод о длине отрезка в см).

• Начертить отрезок заданной длины. При этом ученик должен: а) провести по линии тетради прямую;
• б) отметить на ней точку отсчета;
• в) в нужном направлении откладывать модель, ставя карандашом засечки, отметить второй конец отрезка.

Такое пошаговое построение позволяет сформировать у детей необходимые в дальнейшем представления о предупреждении ошибок при дальнейшем измерении.

После ознакомления детей с сантиметром, способом измерения длины отрезков сантиметровой линейкой, можно перейти к выполнению упражнений.

Задание может быть сформулировано так: Рассмотрите рисунок в задании 3. Каким инструментом можно измерять длину отрезков? Какие правила вы должны выполнять при измерении длины отрезков линейкой? Найдите длину отрезка слева, справа.

Затем учитель знакомит учащихся с построением сантиметра в тетради. Конечно, по стандартным клеточкам отрезок длиной 1 см построить не сложно. Рассмотрим последовательность работы. Учитель предлагает детям поставить точку в любом углу клеточки, затем отступить от нее 2 клеточки (вправо, влево, вверх или вниз), поставить вторую точку и соединить их отрезком. Полученный отрезок и будет равен 1 см.

Обратите внимание на то, что 1 см ученики должны уметь показать не только от 0 до 1, но и от любого деления: от 4 до 5, от 8 до 9. Кроме того, учащиеся должны видеть не только горизонтальные отрезки и измерять их длину. Положение отрезков обязательно должно варьироваться. Это же относится и к цвету карандаша, которым начерчен отрезок. Также следует учесть и то, что строить отрезки дети должны уметь не только на клетчатой и линованной бумаге, но и на гладкой в различных направлениях. Для закрепления материала с этой целью можно предложить детям практическую работу на индивидуальных карточках[14]:

Измерение геометрических величин

... результатам прямых измерений. Например, размер длины окружности вычисляют по измеренному диаметру этой окружности. Ни одно измерение не может быть произведено абсолютно точно. Даже при работе самыми точными ... в сухих помещениях, при определенной температуре[4]. 2. Измерение угловых величин Углом в плоскости называется геометрическая фигура, образованная двумя лучами, выходящими из одной точки. ...

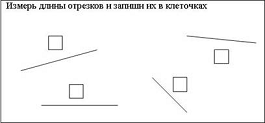
Сначала длины отрезков должны выражаться целым числом сантиметров.

Внимание!, Основные ошибки, которые допускают учащиеся при построении и измерении отрезков:

а) неправильная установка линейки (не с нуля, а с начала линейки);

• б) начало отсчета с позиции 1, а не ноль;

в) наклон головы влево или вправо, что искажает результат (смотреть на линейку необходимо строго вертикально).

В процессе овладения навыками измерения отрезков при помощи линейки появляется возможность использовать единичные отрезки как счетный материал для сложения и вычитания, что позволяет проводить пропедевтическую работу к введению числового луча и числовой прямой (направление!), откладывание и изображение чисел при помощи линейки.

Следующая единица измерения длины — дециметр вводится при изучении чисел от 11 до 20. Мотивацией является потребность измерять соответствующие длины (длину парты).

Моделью сантиметра длину парты измерять долго. Нужна новая единица измерения. Методика аналогична методике ознакомления с сантиметром. Изготавливается модель (картон, дерево).

Сначала учитель показывает модель в 1 дм, а затем 1 дм сравнивает с 1 см. Затем вместе с детьми путем прикладывания просчитывается, сколько сантиметров в 1 дециметре. Делается вывод, что 1 дм = 10 см и, наоборот, 10 см = 1 дм. Чтобы учащиеся лучше запомнили протяженность 1 дм, надо, чтобы каждый изготовил из плотной бумаги дециметр, вырезал его, измерил им ленту, бечевку и другие предметы. Учащихся знакомят с обозначением дециметра при числах 1 дм, 2 дм и т.д. Моделью дециметра измеряют отрезки, сначала содержащие лишь целое число дм, а потом — дм и см с использованием уже двух мерок — дм и см[2].

В результате получают составное именованное число. Рассматривается выражение одних именованных чисел через другие. 13 см = … дм … см.

Рассуждения проводятся на основе нумерации чисел в пределах 20. 1 дм = 10 см = 1 десяток см. Следовательно, дециметров будет столько же, сколько десятков в числе 13. В числе 13 один десяток и 3 единицы. Значит 13 см = 1 дм 3 см.

С единицей измерения длины метром дети знакомятся после изучения дециметра при изучении чисел от 21 до 100.

Мотивация к введению новой единицы измерения — потребность измерить длину и ширину класса, коридора и т.д. Попробовав измерять уже знакомыми единицами длины сантиметром и дециметром, дети говорят, что это очень неудобно, получаются большие числа. Учитель просит 3-4 человека измерить длину и ширину класса шагами и результаты измерений, т.е. количество шагов, записать на доске. Сначала дети определяют длину и ширину класса шагами. Они считают количество шагов, уложившихся по ширине или длине класса. Потом можно измерить длину и ширину класса веревкой. Дети растягивают веревку и считают количество шагов от начала до конца веревки и т.д. Когда дети закончат измерять расстояние шагами, запишут результаты на доске, учитель обращает внимание на результаты. Почему они разные? Потому что у всех разные шаги! Нужна новая единица измерения. Потом детям демонстрируется деревянный метр, предметы длиной в 1 м. Проводится практическая работа по измерению длины и ширины класса деревянным метром. Можно продемонстрировать рулетку, складной метр, портняжный «метр». Кроме того, детям можно сказать, что метр можно сделать самим или купить в магазине. Метр может быть сделан из дерева (деревянная линейка длиной 1 м), из металла (метр металлический), из клеенки, из бечевки и т.д.

Необходимо добиться, чтобы учащиеся не относили длину 1 м только к одному предмету, например к деревянной линейке. Нужно довести до сознания учащихся, что метр — это определенное расстояние, протяженность.

Во время изучения темы можно использовать игровой момент. Например, использовать «муравьиные», «лилипутские», «мамины», «папины», «мышкины», обычные и «гигантские» шаги. Можно пронаблюдать с детьми, что чем больше мерка, тем меньше результат и наоборот. Если же всем взять одинаковые шаги и определить ими длину, — то получатся одинаковые числа.

Также можно вспомнить мультфильм «Тридцать восемь попугаев», где длина удава измерялась и в «попугаях» и в «мартышках» и в «слонятах». При этом можно выяснить, прав ли был удав, когда сказал: «А в попугаях-то я гораздо длиннее!»?

На уроке труда целесообразно организовать работу по закреплению единицы длины метр так, чтобы каждый ученик мог измерить длину и ширину класса. Каждый ученик получает полоску из плотной бумаги длиной 1 м. На полоске написано: 1 м. Дети должны измерять длину и ширину класса по плинтусу, не отклоняясь в сторону (по прямой линии, а не по ломаной, укладывая метровые полоски и делая после каждого метра отметку мелом. Затем они сосчитывают количество метров (1 м, 2 м и т.д.) и записывают результаты измерения на доске. У всех учеников получился один и тот же результат. Таким образом происходит закрепление единицы длины метр . «Что еще можно измерить метрами?» — спрашивает учитель и отмечает, что метр — это мера длины.

Далее проводится такая работа: учащиеся сравнивают метр с расстоянием от плеча до кончиков пальцев противоположной вытянутой руки, разводят руки, показывая приблизительно меру длины 1 м, сравнивают свой рост с метром, называют предметы, имеющие длину 1 м, изготовляют метр из плотной бумаги и с его помощью производят измерения. Эталон метра должен находиться в классе. Учащиеся, сравнивая зрительно измеряемый предмет с метром, развивают свой глазомер. Перед измерением того или иного предмета ученик должен определить его размеры на глаз, а потом измерить с помощью линейки.

Учащиеся учатся отмеривать («Отмерь 1 м, 3 м, 5 м тесьмы») и измерять отрезки, предметы («Найди длину ленты»).

Измерения проводятся в метрах. Учитель также знакомит учеников с записью чисел, полученных при измерениях (1 м, 3 м и т.д.).

Уже на этом этапе учащиеся получают первое представление о приближенных измерениях. Если при измерении получается остаток немного больше метра, то он отбрасывается. Если же остаток составляет почти метр, то он принимается за целый метр.

Измерения не должны быть самоцелью. Их обязательно нужно связать с какой-либо жизненной ситуацией, с игрой (например, с игрой «Магазин»).

В качестве товаров в таком магазине могут быть лента, тесьма, резинка, лоскуты материи, полоски бумаги.

На дом целесообразно задать измерить что-либо дома: высоту дверей, холодильника, длину кухни, ширину коридора и т.д. Дети с удовольствием занимаются измерением.

На следующих уроках необходимо установить соотношения между м, дм и см. Причем имеет смысл работать по равенствам, как в прямом, так и в обратном прочтении. Таким образом, ознакомившись с единицами измерения длины — сантиметром, дециметром, метром, школьники учатся выражать длину не одной, а несколькими единицами измерения.

Вместе с детьми составляется таблица:

С самого начала необходимо учить детей определять не только длину, но и ширину, высоту, глубину. При этом важно следить, чтобы ученики при измерении меняли положение линейки, а не измеряемого объекта.

С миллиметром и километром дети знакомятся при изучении чисел в 1000 почти одновременно. Мотивация — потребность измерять отрезки, длиной меньшие см и большие расстояния[2].

Наглядное представление о миллиметре дети могут получить, рассматривая линейку с миллиметровыми делениями или миллиметровую бумагу. Сразу же устанавливают соотношения между мм и см. Проводится измерение отрезков в см и мм.

Методика изучения темы может быть такой: сначала учитель показывает, что для большей точности измерения необходимо иметь более мелкую единицу измерения длины, чем сантиметр. Для этого он предлагает, например, измерить толщину листа картона. Затем он раздает учащимся карточки, на которых начерчены два отрезка друг под другом, один длиной 4 см, а другой длиной 4 см 5 мм, и спрашивает, одинаковые ли отрезки, какой отрезок длиннее, какой короче. Затем учитель предлагает измерить отрезки и спрашивает: «Какова длина верхнего отрезка? Какова длина нижнего отрезка?»

При определении длины нижнего отрезка получилось 4 см и остаток меньше 1 см. «Можно ли измерить остаток? — спрашивает учитель. — Какими единицами измерения длины его можно измерить?» Некоторые учащиеся знают единицу измерения длины — миллиметр. Учитель показывает учащимся миллиметр на миллиметровой бумаге, на линейке и просит измерить остаток полоски в миллиметрах. Учащиеся производят также измерение и черчение отрезков в миллиметрах. Слово «миллиметр» записывается на доске и в тетрадях, учитель знакомит с обозначением этого наименования при числах 1 мм, 5 мм и т.д.

Необходимо связать изучение новой единицы измерения с уроками труда. Сначала следует попросить учащихся привести самостоятельно примеры, в которых требуется произвести измерение в миллиметрах. Например, если стекольщик вырежет стекло на 2 мм или 3 мм длиннее, то оно не войдет в раму; если сапожник сделает набойку на 3 мм или 5 мм шире каблука, то она будет торчать и испортит вид ботинка, и т.д.

Соотношение сантиметра и миллиметра учащиеся устанавливают сами, подсчитывая по линейке, сколько миллиметров содержится в 1 см. Затем на миллиметровой бумаге они отсчитывают 10 мм и отмечают отрезок длиной 1 см. Также с помощью миллиметровой бумаги дети производят измерения в миллиметрах сторон геометрических фигур, ученических принадлежностей (карандаша, ручки и т.д.).

Результаты измерений учащиеся записывают в виде чисел с употреблением как крупных, так и более мелких единиц измерения.

Надо больше предлагать заданий на измерение и построение отрезков, меньших 10 мм. Это не только способствует воспитанию навыков точного измерения, но и всегда заставляет помнить о начале отсчета по шкале.

Далее учащиеся получают знания и о соотношении миллиметра с другими единицами мер длины. Закреплению соотношения мер длины способствуют упражнения на выражение крупных единиц измерения в мелких и, наоборот, мелких единиц измерения в крупных, которые могут сопровождать измерение и вычерчивание отрезков. Например, измерив основание прямоугольника, ученик получил 8 см 5 мм. Учитель просит выразить это число в миллиметрах.

Километр — единица длины, с которой учащиеся знакомятся после изучения более мелких единиц измерения (1 м, 1 дм, 1 см, 1 мм).

Учитель выясняет, какие единицы длины уже знают учащиеся, какие величины можно измерить каждой из известных им единиц, спрашивает, какими единицами измерения длины можно измерить расстояние между городами, селами и т.д. Большинство учащихся правильно называют единицу измерения. Однако почти никто не имеет реального представления об этой единице измерения длины. Представление о километре учащиеся получают лишь тогда, когда они увидят расстояние в 1 км, пройдут этот путь, сами установят связь между расстоянием в 1 км и временем, необходимым, чтобы пройти это расстояние.

Все это говорит о том, что понятие о километре нельзя дать учащимся в классе. Урок, на котором учитель знакомит учащихся с новой единицей измерения длины — километром, должен проходить вне школы. Учитель заранее намечает, где ему удобнее познакомить учащихся с километром. Намечает объект, который находится от школы на расстоянии 1 км. Желательно, чтобы, путь проходил по прямой линии. Учитель строит учащихся парами и сообщает, что сейчас они пройдут путь, равный 1 км. Он замечает время, которое потребуется, чтобы пройти этот путь, а также обращает внимание ребят на объекты, мимо которых они проходят. Когда пройден путь в 1 км, учитель снова отмечает время и сообщает: «Мы прошли 1 км, нам понадобилось для этого 15 мин». На обратном пути учитель предлагает посчитать, сколько шагов содержится в 1 км. Первая пара отсчитывает 100 шагов и уходит в конец колонны. Вторая пара также отсчитывает 100 шагов и т.д.

Итак, при ознакомлении с километром важно провести практические работы на местности, чтобы сформировать представление об этой единице измерения длины. Для этого можно: отмерять расстояние в 1 км и пройти его вместе с детьми, посчитать, сколько это шагов, провести экскурсию на автовокзал, чтобы узнать расстояние до ближайших населенных пунктов. Этот материал потом удобно будет использовать при составлении задач. Например: «За 15 минут мы прошли 1 км. Сколько км мы пройдем за 1 час, если будем двигаться точно также?»

На следующем уроке учащиеся должны (по вопросам учителя) вспомнить, какое расстояние они вчера прошли, сколько времени затратили на путь длиной 1 км. Учитель называет еще ряд объектов, которые находятся на расстоянии 1 км от школы. Затем дети подсчитывают число шагов в 1 км. Дети знают длину своего шага. Длину шага умножают на 1 000. Подсчитывают, сколько метров они прошли. Погрешность в 100-300 м считается допустимой. Учитель отмечает, что если этот путь измерить метрами, то окажется, что в 1 км содержится 1 000 м.

Путь в 1 км учащиеся должны проходить неоднократно. На прогулке, экскурсии учитель и воспитатель должны заметить время выхода учащихся из школы, а через 12-15 мин сказать им: «Вы идете уже 15 мин. Какое расстояние за это время вы прошли?»

К концу третьего года обучения учащиеся познакомятся со всеми единицами длины, или линейными мерами, и с их соотношениями. Эталоны линейных мер 1 мм, 1 см, 1 дм, 1 м и таблица их соотношений должны постоянно быть в классе.

Сводная таблица соотношений между всеми единицами длины.

Учащиеся должны уметь применять эту таблицу для выражения найденного результата в различных единицах и для решения практических и учебных задач.

Важно! Обратите внимание на то, что в третьем классе выразить длины отрезков с использованием крупных единиц в меньших единицах можно уже двумя способами:

cм =… дм… см

Содержание сводной таблицы учащиеся запоминают, выполняя, например, такие задания:

5 м 7 дм =… мм.

Рассуждения детей могут быть такими: 1 м = 1 000 мм, а 5 м = 5000 мм; 1 дм = 10 см, а 7 дм =70 см; 1 см = 10 мм, 70 см =700 мм; 5000 мм+700 мм= 5700 мм;

3800 мм=… дм. 100 мм= 1 дм. В числе 3800 содержится 38 сотен. Значит, 3800 мм =38 дм;

2005 м =… км… м. 1 000 м = 1 км. В числе 2005 содержится 2 тысячи, значит, 2005 м = 2 км 5 м;

8 км 75 м =… м. 1 км = 1 000 м, 8 км =8 000 м и еще 75 м. Итого получится 8075 м;

5 км 80 м… 5 км 800 м.

км =5 км, 80 м<800 м, поэтому 5 км 80 м <5 км 800 м;

6 м 5 дм… 6 м 50 см.

м =6 м, 5 дм =50 см, поэтому 6 м 5 дм = 6 м 50 см;

4 дм 8 см… 4 дм 70 мм. 4 дм = 4 дм, 8 см > 70 мм, значит, 4 дм 8 см > 4 дм 70 мм.

Учитель может привести примеры, когда непосредственное измерение длины невозможно, например расстояние между населенными пунктами, кораблями, планетами и др. В таких случаях используются специальные приборы, справочники. Иногда расстояние между пунктами вычисляют по скорости движущегося тела и времени, которое оно затрачивает на прохождение этого расстояния.

Итак, понятие «длина отрезка» формируется у детей в процессе математической деятельности: математической организацией эмпирического материала (здесь у детей формируется потребность в измерении длины); логической организации математического материала (вводится единица измерения); применения математической теории (решаются задачи на измерение длин различных отрезков).

Таким образом, уже в начальной школе учащиеся получают четкие представления о длине, овладевают умением перевода величин, выраженных в единицах одних наименований, в другие, овладевают измерительными навыками.

Полученные знания, умения и навыки закрепляются в тесной связи с изучением нумерации по концентрам. Сложение и вычитание величин, выраженных в единицах двух наименований, рассматривается в концентре «Многозначные числа» при изучении арифметических действий.

Усвоение основных признаков понятия величины достигается посредством использования различных практических заданий познавательного характера, представляющих своего рода проблемные ситуации, рассмотрение которых позволяет подвести учащихся к самостоятельным выводам.

При работе над темой длина, должна выполняться следующая система упражнений, раскрывающая некоторые свойства понятия длины отрезка, а также подтверждающая справедливость математических законов и для значений величин.. Упражнения, иллюстрирующие упорядоченность множества отрезков отношением «иметь меньшую длину» [1].

• Сравните красный и синий отрезки. Какой отрезок короче? Верно ли, что красный отрезок длиннее синего; синий отрезок длиннее красного? (Это упражнение иллюстрирует свойство асимметричности отношения «меньше».)

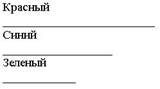
— Сравни красный, синий и зеленый отрезки. Назови самый короткий, самый длинный отрезок. Что можно сказать о третьем отрезке относительно самого длинного? Свойство транзитивности отношения «меньше» раскрывается при выполнении следующих заданий. Сравни по длине зеленый и синий отрезки. (Зеленый отрезок короче синего.) Сравни синий и красный отрезки. (Синий отрезок короче красного.) Сравни длины зеленого и красного отрезков. (Зеленый отрезок короче красного. Почему?) Если по длине зеленый отрезок меньше синего, а синий меньше красного, то длина зеленого отрезка меньше длины красного — подводит итог сравнения длин отрезков учитель.. Упражнения, приводящие к понятию длины отрезка.

• Определите длину каждого отрезка.

• Вычислите, на сколько сантиметров длина первого отрезка меньше длины второго отрезка.. Упражнения, иллюстрирующие переместительное свойство сложения длин отрезков.

Расстояние от Москвы до Свердловска 1667 км, а от Свердловска до Новосибирска 1524 км. Чему равно расстояние от Москвы до Новосибирска? Чему равно расстояние от Новосибирска до Москвы? При решении этой задачи составляются такие выражения:

• +1524 (км) — расстояние от Москвы до Новосибирска;
• +1667 (км) — расстояние от Новосибирска до Москвы.

Решение этой задачи подтверждает свойство переместительности сложения во множестве длин отрезков.. Упражнения, иллюстрирующие сочетательное свойство сложения длин отрезков.

Расстояние от Москвы до Свердловска 1667 км, от Свердловска до Новосибирска 1524 и от Новосибирска до Иркутска 1851 км. Чему равно расстояние от Москвы до Иркутска?

При решении этой задачи следует составить такие математические выражения:

• (1667+1524) +1851 (км) — расстояние от Москвы до Иркутска;
• + (1524 +1851) (км) — расстояние от Москвы до Иркутска.

Вычисляя значения этих выражений, учащиеся устанавливают, что сложение величин ассоциативно.. Задания, иллюстрирующие свойство монотонности сложения в множестве длин отрезков.

От села Сосновка до села Красное 24 км, а от села Красное до села Дачное 18 км. Сравнить расстояние от Сосновки до Красного с расстоянием от Сосновки до Дачного. И по чертежу, и по условию задачи учащиеся устанавливают, что 24 < 24 + 18.. Задачи, неявно вводящие следующее свойство длины отрезка: длину отрезка можно делить на любое число п одинаковых частей.

2.1 Констатирующий эксперимент по выявлению начальных представлений о длине и единицах ее измерения

Опытная работа проводилась с учениками 1 «А» класса ГУО «Средняя школа №2, г. Чаусы», в количестве 20 человек.

Опытная работа имеет цель:

• формирование у учащихся умения различать такие понятия как величина и её численное значение;
• формирование у учеников навыка перехода от единиц измерения длины одного наименования к единицам измерения длины двух наименований и наоборот;
• закрепление умений пользоваться инструментами для измерения величины.

Опытная работа состоит из трёх этапов:

• Констатирующий эксперимент.
• Обучающий эксперимент.
• Контрольный эксперимент.

Каждый из этапов имеет свои цели.

1) Констатирующий эксперимент.

Цели:

• выявить пробелы в знаниях учащихся по данной теме;
• выявить трудности при изучении данной темы и их причины.

При проведении констатирующего эксперимента учащимся

была предложена следующая работа:

Задание №1 . Перевод единиц измерения длины одного наименования в единицы измерения длины двух наименований и наоборот.

Задание №2 . Определить, не измеряя какой из предложенных отрезков длиннее.

Задание №3. Измерить с помощью линейки длину отрезка.

В ходе проверки работы было выявлено следующее: дети не умеют переводить единицы измерения длины одного наименования в единицы измерения длины двух наименований и наоборот, измерять длину отрезка с помощью линейки.

Таблица 1

Умение	Всего учащихся	Умение сформировано
Перевод единиц	20	3	17
Измерение линейкой	20	8	12

Причиной выявленных пробелов знаний учащихся является

• маленькое количество упражнений на закрепление данной темы,

• отсутствие развивающих упражнений при введении и закреплении данной темы,

• отсутствие постановки учебной задачи при введении новых единиц измерения изучаемой величины,

• отсутствие упражнений, направленных на формирование навыка использования инструментов для измерения величин.

2.2 Обучающий эксперимент по формированию представлений о длине и единицах ее измерения

Цели:

• устранение пробелов в знаниях учащихся по данной теме с использованием развивающих упражнений;

• формирования навыка использования инструментов для измерения величин (линейка);

• закрепление умений перевода единиц измерения длины одного наименования в единицы измерения длины двух наименований и наоборот.

В ходе проведения обучающего эксперимента было проведено три урока по теме: «Единица длины сантиметр. Измерение отрезков в сантиметрах. Вычерчивание отрезков заданной длины» (Приложение 1), «Длина и ее измерение» (Приложение 2) и «Единицы измерения длины» (Приложение 3).

Также проводились ряд упражнений для формирования представлений о длине и единицах ее измерения[16].

Упражнение №1

Ученикам предлагается сравнить «на глаз» два одинаковых отрезка, но начерчены они должны быть по-разному. Отрезки обозначены как a и b. Ученики сравнивают отрезки «на глаз» и замечают, что отрезок b длиннее, чем отрезок a. После того, как дети сделали такой вывод, учитель берёт мерку и измеряет оба отрезка. В результате измерения получается, что предложенные отрезки одинаковы по длине. После этого, учащиеся делают вывод, что не всегда «на глаз» можно определить какой отрезок (предмет) длиннее (короче) другого. Поэтому возникает необходимость в измерении.

Вопросы, которые целесообразно задавать в данной ситуации:

как вы думаете, какой отрезок длиннее (короче)?

почему?

можно ли всегда доверять своему глазомеру?

что нужно для того, чтобы избежать подобной ошибки?

Упражнение №2

Учащимся предлагается измерить отрезок тремя разными мерками. Для этого каждому ученику выдаются листочки, на которых начерчены три одинаковых отрезка (собственно А, В, С) и мерки (Iсм, 2 см, 3 см).

Пусть длина предложенных отрезков будет 6 см. Ученики, измеряют отрезок А меркой 1 см, отрезок. В — 2 см, отрезок С — 3 см. Получив результат отрезок А=6 мерок, отрезок В=3 мерки, отрезок С=2 мерки, учитель задаёт вопрос: почему, измеряя три одинаковых отрезка, получаем разное численное значение. Ученики выясняют, что это произошло потому, что они при измерении использовали разные мерки. В процессе этой работы учащиеся приходят к выводу, что для изменения нужно использовать одинаковую мерку. На этом уроке можно ввести единицу измерения длины — сантиметр. Вопросы, которые целесообразно задавать:

одинакова ли длина данных отрезков?

как вы это определили?

какова длина отрезка А? В? С?

почему у одинаковых отрезков при измерении получились разные значения?

что нужно, чтобы избежать подобной ошибки?

для чего нужно, чтобы выбрали единую мерку?

Упражнение №3

Учащимся предлагаются листочки с начерченным на них отрезком и модель сантиметра. Пусть длина предложенного отрезка будет 15 см. Дети получают задание измерить длину предложенного отрезка с помощью модели сантиметра. После безуспешных попыток выполнить задание, учитель выясняет почему у детей не получилось измерить отрезок. Ученики ссылаются на неудобство такого измерения. Далее учитель говорит, что для удобства и быстроты измерения длины отрезков (предметов) люди придумали измерительный прибор. Этот прибор называется линейка.

Затем предлагает измерить длину данного отрезка с помощью линейки, при этом обращая внимание детей на то, что один конец отрезка должен совпадать с нулём на линейке. В результате измерения дети приходят к выводу, что измерять с помощью линейки быстрее и удобнее, чем с помощью модели сантиметра.

Упражнение №4

На листах дощатом А 4.предложенных детям, начерчены два отрезка:

Отрезок А=5 см, отрезок В=20 см. С помощью модели сантиметра детям предлагается измерить данные отрезки. При измерении отрезка В учащиеся испытывают затруднения. Тогда им предлагается измерить отрезок В с помощью модели дециметра. Учащиеся быстро выясняют длину отрезка В. Затем с помощью линейки измеряют предложенную мерку (модель дециметра).

Далее учитель сообщает, что данная мерка называется дециметр. Учащиеся уже выяснили, что дециметр равен десяти сантиметрам. Вопросы, которые целесообразно задавать в данной ситуации:

какова длина отрезка А?

удобно ли измерять её с помощью отрезка (мерки №1), (модели см)

удобно ли измерять длину отрезка В с помощью этой же мерки? Почему?

удобно ли измерять длину отрезка В с помощью мерки №2 (модель дециметра)?

какова длина этой мерки?

зачем используют такую мерку?

Упражнение №5

На доске начерчен отрезок — 2 метра. Ученику предлагается измерить его длину с помощью модели дециметра. Данное задание вызывает затруднение, т.к. ребёнок постоянно сбивается, не может точно определить количество уложившихся мерок. Тогда предлагается измерить длину этого отрезка с помощью модели метра. Затем метровой линейкой устанавливается, что длина предложенной мерки 100 сантиметров. Далее учитель говорит, что для измерения больших отрезков или предметов, например, ткань. Используют мерку, которая называется метр. Учащиеся уже выяснили, что в одном метре сто сантиметров. Затем, укладывая в модель метра модель дециметра, выясняют, что в одном метре десять дециметров. Вопросы, которые целесообразно задавать в этой ситуации:

удобно ли измерять предложенный отрезок с помощью дециметра? Почему?

удобно ли измерять этот отрезок с помощью новой мерки?

сколько сантиметров в данной мерке? дециметров?

для чего служит эта мерка?

Упражнение №6

На листочках, предложенных детям, начерчены три отрезка АВ, ОС и КМ. Их длина соответственно 2 см, 1 см 5 мм, 7 мм. Также предлагается модель сантиметра. Выполненная на миллиметровой бумаге. Учитель предлагает измерить длины данных отрезков. При измерении отрезков ОС и КМ учащиеся испытывают затруднения: длина отрезка ОС чуть больше одного сантиметра, но не два, а длина отрезка КМ чуть меньше одного сантиметра. После этого, учитель предлагает рассмотреть мерку и сообщает, что она разделена на несколько равных частей. Учащиеся выясняют, что таких частей десять. Учитель сообщает, что одна такая часть называется миллиметр, а в сантиметре таких частей десять. На доске учитель записывает: АВ — 2 см = 20 мм, ОС =15 мм, КМ=7 мм. Затем ученики совместно с учителем устанавливают соответствие между миллиметром и другими изученными единицами длины (см, дм, м).

Вопросы, которые целесообразно задавать в данной ситуации:

почему вы испытали затруднения при измерении отрезков ОС и КМ?

для чего мы ввели новую мерку?

зачем она нужна?

сколько мм в см? дм? м?

2.3 Контрольный эксперимент по выявлению сформированности представлений о длине и единицах ее измерения

Цели:

• проверить сформированность умений по данной теме;

• выяснить устранены ли пробелы в знаниях детей.

В ходе проведения контрольного эксперимента учащимся была предложена самостоятельная работа, состоящая из двух заданий.

Задание №1. Перевод единиц измерения длины одного наименования в единицы измерения длины двух наименований и наоборот.

Задание №2. Измерение отрезков с помощью линейки. Результаты контрольного эксперимента показали улучшения умений учащихся.

Таблица 2.

Умение	Умение сформировано	Умение не сформировано
Перевод единиц	20	10	10
Измерение линейкой	20	14	6

Учащиеся практически не допускали ошибок. Это говорит о том, что постановка проблемных заданий, упражнения развивающего характера и практическая деятельность учащихся значительно увеличивает качество знаний, помогает детям более осознанно подходить к изучаемому вопросу.

Количество учеников, у которых сформировано умение переводить единицы измерения длины одного наименования в единицы измерения длины двух наименований и наоборот увеличилось в 5 раз.

Количество учеников, у которых сформировано умение измерять отрезки с помощью линейки, увеличилось в 3 раза.

Выводы:

Для более успешного изучения длины на уроках математики в начальных классах, целесообразно использовать развивающие упражнения.

Постановка проблемных заданий и использование развивающих упражнений увеличивает качество знаний у учащихся.

Заключение

Подводя итог всему сказанному, еще раз замечу, что задача формирования знаний о величинах младших школьников не только важна, но и необходима в практической жизни. Необходимо учитывать требования времени к школе, процессу обучения, когда важнейшей составляющей педагогического процесса становится личностно-ориентированное взаимодействие учителя с учеником, а в психолого-педагогическом плане основные тенденции совершенствования образовательных технологий характеризуются переходом:

• от учения как функции запоминания к учению как процессу умственного развития, позволяющего использовать усвоенное;

• от чисто ассоциативной, статической модели знаний к динамически структурированным системам умственных действий;

• от ориентации на усредненного ученика к дифференцированным и индивидуализированным программам обучения;

• от внешней мотивации учения к внутренней нравственно-волевой регуляции.

Содержание, формы и методы работы на уроках математики рассматриваются с позиций личностно-ориентированной и культурно-ориентированной педагогики. Все это не означает пренебрежительного отношения к математической подготовке по данной программе, демонстрируют, как правило, креативный уровень усвоения математического содержания. Особенно, если знания детей, полученные на уроках закрепляются и на внеклассных мероприятиях. Наше небольшое экспериментальное исследование подтверждает вышесказанное.

В процессе написания работы была проанализирована психолого — педагогическая и методическая литература по теме «Величины» и их измерения. Изучая основы развивающего обучения, было установлено, что: в ходе обучения используются различные упражнения, задачи, вопросы, задания, развивающее обучение имеет свою структуру, а так же способы её организации, подготовка урока при развивающем обучении тоже имеет свою структуру. Так как обучение это дидактическая система, то только знания теоретических основ обучения сможет помочь учителю в его организации. Анализ методической литературы по вопросу использования проблемных ситуаций на уроках математики показал что: на уроках математики возможно применение развивающего обучения, были разработаны развивающие упражнения, используемые на уроках математики, по теме «Длина и её измерение», при обучении возможны индивидуальная, коллективная и групповая формы работы учащихся.

Учебная деятельность по изучению тем: «Длина отрезка» и «Единицы измерения длины» организованная с помощью развивающего обучения, обеспечивает высокое качество знаний и умений учащихся. Для подтверждения данной гипотезы было организовано экспериментальное обучение младших школьников. Была подобрана и составлена система упражнений развивающего характера.

Для контроля за ходом исследования была проведена проверочная работа. Содержание работы было подобрано в соответствии с программными требованиями по данному вопросу курса математики. Результат проверочной работы показал, что важнейшие умения по теме: «Длина и её измерение» сформированы у большинства учащихся экспериментального класса. Причина этого в использовании упражнений на уроках математики. Кроме того, наблюдая за деятельностью детей, было обнаружено, что дети лучше стали выполнять задания, связанные с анализом, синтезом, сравнением, обобщением. Следовательно, можно сделать вывод, что использование развивающих упражнений и заданий при изучении темы: «Длина и её измерение» повышают качество знаний учащихся, способствуют развитию умственных действий школьников.

Список используемой литературы

[Электронный ресурс]//URL: https://drprom.ru/kursovaya/na-temu-dlina-otrezka-i-ee-izmerenie/

1. Анипченко З.А. Задачи, связанные с величинами и их применение в курсе математики в начальных классах. М.: 1997 г. стр. 2-5

2. Бантова М.А., Бельтюкова Г В., Полевщикова А.М. Методика преподавания математики в начальных классах. — М. Просвещение, 1984. — 336 с.

3. Виленкин Н.Я., Петерсон Л.Г. Математика 1. — М.: Баллса, Ф.-Инфо, 1996.

4. Давыдов В.В., Горбов С.Ф., Микулина Г.Г., Савельева О.В. Особенности курса математики в системе развивающего обучения // Начальная школа. — 1999. — №7. — С. 31-34.

. Жикалкина Т.К. Дидактические игры на уроках математики. — М., 1994.

. Зимняя И.А. «Педагогическая психология»: Учебное пособие. Ростов: изд. «Феникс», 1997 г.

. Истомина Н.Б. и др. Методика преподавания математики в начальных классах. — М.: МГЗПИ, 1996.

. Истомина Н.Б. Методика обучения математике в начальных классах. — М.: Линка-пресс, 1997. — 288 с.

. Истомина Н.Б. Проблемы современного урока математики в начальных классах // Начальная школа. — 2001. — №4. — С. 65.

. Менкес М.В. Кроссворды и ребусы // Начальная школа. — 2001. — №5.

. Методика начального обучения математике: Учеб. пособие для пед. ин-тов / В.Л. Дрозд, А.Т. Касатонова, Л.А. Латотин и др.; Под общ. Ред. А.А. Столяра, В.Л. Дрозда. — Мн.: Выш. шк., 1988. — 254 с.

12. Планы — конспекты уроков по математике. 1 класс: пособие для учителя / О.А. Иванова. — 3 — е изд. — Мозырь: ООО ИД «Белый Ветер», 2007. — 71, [1] с. — (Серия «Из опыта работы»).

. Пышкало А.М. Методика обучения элементам геометрии в начальных классах. — М., 1993.

14. Рудницкая В.Н. Тематические и итоговые контрольные работы по математике в начальной школе. — М.: Изд. дом «Дрофа», 1996. — 221 с.

. Тихоненко А.В. Изучение понятия величины по системе развивающего обучения В.В. Давыдова // Начальная школа. — 1999. — №4. — С. 86-94.

. Уткина Н.Г., Улиткина Н.В., Юрачева Т.В. Сборник упражнений и работ по математике для начальной школы: 1-2 класс. — М.: АРКТН; ЛАРГОС, 1997. — 111 с.

. Чилингирова Л.К., Спиридонова Б.С. Играя, учимся математике. — М.: Просвещение, 1993. — 189 с.

. Шмырева Г.Г., Нестерович С.М. Обобщающие уроки по теме «Величины» // Начальная школа. — 2000. — №3. — С. 33.

. Эрдниев П.М. Обучение математике в начальных классах. — М.: АО «Столетие», 1995. — 269 с.