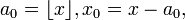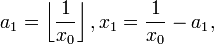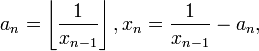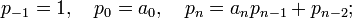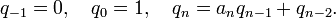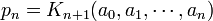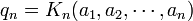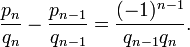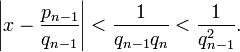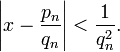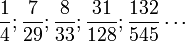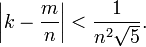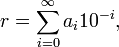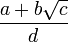где a 0 есть целое число и все остальные a n натуральные числа (то есть неотрицательные целые).
Любое вещественное число можно представить в виде цепной дроби (конечной или бесконечной).
Число представляется конечной цепной дробью тогда и только тогда, когда оно рационально. Число представляется периодической цепной дробью тогда и только тогда, когда оно является квадратичной иррациональностью.
1. Разложение в цепную дробь
Любое вещественное число x может быть представлено (конечной или бесконечной) цепной дробью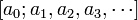 
, где
где 
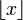обозначает целую часть числа x .
Для рационального числа x это разложение оборвётся по достижении нулевого x n для некоторого n. В этом случае x представляется конечной цепной дробью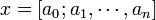 
.
Для иррационального x все величины x n будут ненулевыми и процесс разложения можно продолжать бесконечно. В этом случае x представляется бесконечной цепной дробью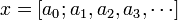 
.
Для рациональных чисел может быть использован алгоритм Евклида для быстрого получения разложения в цепную дробь.
2. Подходящие дроби
подходящей дробью
Эйлер вывел рекуррентные формулы для вычисления числителей и знаменателей подходящих дробей:
Таким образом, величины p n и q n представляются значениями континуант:
Траншейный цепной экскаватор на гусеничном ходу с глубиной копания до 4м
... ковши); Скребковые (с однорядной или двухрядной цепью, оборудованной резцами и скребками). Цепные траншейные экскаваторы могут быть использованы как дополнительное сменное рабочее оборудование на трактор или ... мощности базового трактора 10 через трехступенчатый редуктор 8 с переменным передаточным числом, обеспечивающим четыре рабочие скорости (0,8...2,1 м/с) и реверсивный ход цепи. В ...
Последовательност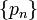и 
и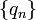 
являются возрастающими.
Числители и знаменатели соседних подходящих дробей связаны соотношением:
| p n q n — 1 — q n p n — 1 = ( — 1)n — 1 , | (1) |
которое можно переписать в виде
Откуда следует, что
3. Приближение вещественных чисел рациональными
Цепные дроби позволяют эффективно находить хорошие рациональные приближения вещественных чисел. А именно, если вещественное число x разложить в цепную дробь, то её подходящие дроби будут удовлетворять неравенству
Отсюда, в частности, следует:
3.1. Примеры
- Разложим число π =3,14159265… в непрерывную дробь и подсчитаем его подходящие дроби:
- 3, 22/7, 333/106, 355/113, 103993/33102, …
- Вторая дробь (22/7) — это известное архимедово приближение. Четвёртая (355/113) была впервые получена в Древнем Китае.
4. Свойства и примеры
- Любое рациональное число может быть представлено в виде конечной цепной дроби двумя способами, например:
- Теорема Лагранжа : Число представляется в виде бесконечной периодической цепной дроби тогда и только тогда, когда оно является иррациональным решением квадратного уравнения с целыми коэффициентами.
- Например:
-
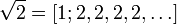
- золотое сечение
-
-
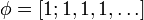
- e − 1 = [1;1;2;1;1;4;1;1;6;1;1;8;…;1;1;2n − 2;1;1;2n ;…]
для числа
- У числа пи простой закономерности не видно:[2]
-
- π = [3; 7, 15, 1, 292, 1, 1, 1, 2, 1, 3, 1, 14, 2, 1, 1, 2, 2, 2, 2, 1, 84, 2, 1, 1, 15,…]
- Теорема Гаусса — Кузьмина: Почти для всех (кроме множества меры нуль) вещественных чисел существует среднее геометрическое коэффициентов соответствующих им цепных дробей, и оно равно постоянной Хинчина.
- Теорема Маршалла Холла. Если в разложении числа x в непрерывную дробь, начиная со второго элемента не встречаются числа большие n , то говорят, что число x относится к классу F (n ). Любое вещественное число может быть представленно в виде суммы двух чисел из класса F (4) и в виде произведения двух чисел из класса F (4). [3] В дальнейшем было показано, что любое вещественное число может быть представленно в виде суммы 3 чисел из класса F (3) и в виде суммы 4 чисел из класса F (2). Количество требуемых слагаемых в этой теореме не может быть уменьшено — для представления некоторых чисел указанным образом меньшего количества слагаемых недостаточно.[4] [5]
5. Приложения цепных дробей
5.1. Теория календаря
При разработке солнечного календаря необходимо найти рациональное приближение для числа дней в году, которое равно 365,2421988… Подсчитаем подходящие дроби для дробной части этого числа:
Первая дробь означает, что раз в 4 года надо добавлять лишний день; этот принцип лёг в основу юлианского календаря. При этом ошибка в 1 день накапливается за 128 лет. Второе значение (7/29) никогда не использовалось. Третья дробь (8/33), то есть 8 високосных лет за период в 33 года, была предложена Омаром Хайямом в XI веке и положила начало персидскому календарю, в котором ошибка в день накапливается за 4500 лет (в григорианском — за 3280 лет).
Очень точный вариант с четвёртой дробью (31/128, ошибка в сутки накапливается только за 100000 лет) пропагандировал немецкий астроном Иоганн фон Медлер (1864), однако большого интереса он не вызвал.
5.2. Решение сравнений первой степени
Рассмотрим сравнени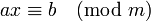е: 
, где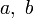 
известны, причём можно считать, что a взаимно просто с m . Надо найти x .
Разложим 
в непрерывную дробь. Она будет конечной, и последняя подходящая дробь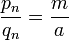 
. Подставим в формулу (1):
- mq n − 1 − ap n − 1 = ( − 1)n − 1
Отсюда вытекает:
-
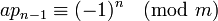, или: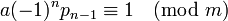 
Вывод: класс вычетов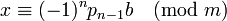 
является решением исходного сравнения.
5.3. Другие приложения
5.3.1. Свойства золотого сечения
Интересный результат, которые следует из того факта, что выражение непрерывной дроби для φ не использует целых чисел больше чем 1, состоит в том, что φ является одним из самых «трудных» действительных чисел для приближения с помощью рациональных чисел. Одна теорема (Теорема Гурвица) [7] утверждает, что любое действительное число k может быть приближено дробью m /n при помощи
Тогда когда практически все действительные числа k имеют в конечно счёте бесконечно много приближений m /n , которые находятся на значительно меньшем расстояние от k , чем этот предел, приближения для φ (т.е. числа 5/3, 8/5, 13/8, 21/13, и т.д.) последовательно «касаются границы», удерживая расстояние на почти точно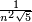 
расстоянии от φ, тем самым никогда не создавая приближения столь же внушительные как, к примеру, 355/113 для π. Может быть показано что любое действительное число формы (a + b φ)/(c + d φ) – где a , b , c иd являются целыми числами, такими как ad − bc = ±1 – имеют такое же свойство как и золотое сечение φ; а также, что все остальные действительные числа могут быть приближены намного лучше.
6. Историческая справка
Античные математики умели представлять отношения несоизмеримых величин в виде цепочки последовательных подходящих отношений, получая эту цепочку с помощью алгоритма Евклида. По-видимому, именно таким путём Архимед получил приближение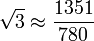 
— это 12-я подходящая дробь для 
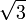или от 4-й подходящей дроби для 
.
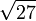В V веке индийский математик Ариабхата применял аналогичный «метод измельчения» для решения неопределённых уравнений первой и второй степени. С помощью этой же техники было, вероятно, получено известное приближение для числа π (355/113).
В XVI веке Рафаэль Бомбелли извлекал с помощью цепных дробей квадратные корни (см. его алгоритм).
«непрерывная дробь»
Применялись эти дроби в первую очередь для рационального приближения вещественных чисел; например, Христиан Гюйгенс использовал их для проектирования зубчатых колёс своего планетария. Гюйгенс уже знал, что подходящие дроби всегда несократимы и что они представляют наилучшее рациональное приближение.
В XVIII веке теорию цепных дробей в общих чертах завершили Леонард Эйлер и Жозеф Луи Лагранж.
7. Мотивация
Непрерывные дроби являются самыми «математически естественными» представлениями вещественных чисел.
Большинство людей знакомы с десятичным представлением вещественных чисел, которое может быть определено как
где a 0 может быть любым целым числом, а последующие ai являются одним из элементом {0,1,2,…,9}. В этом представление, число π, к примеру, может быть представлено как последовательность целых чисел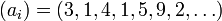 
.
Это десятичное представление имеет несколько проблем. Одна из них, многие рациональные числа не имеет конечного представления в этой системе. Например, число 1/3 представимо бесконечной последовательностью (0,3,3,3,3,…).
Другая проблема заключается в том, что константа 10 является по сути произвольным выбором, который оказывает предпочтение числам, которые как-либо относятся к целому числу 10. Например, 137/1600 имеет конечное десятичное представление, тогда как 1/3 не имеет, не потому, что 137/1600 проще чем 1/3, а всего лишь потому, что 1600 делит степень 10 (10 6 = 1600 × 625).
Запись как цепная дробь является представлением вещественных чисел, которая не имеет этих проблем.
Давайте рассмотрим как мы можем описать число, такое как 415/93, которое примерно равняется 4,4624. Это примерно 4.Вообще-то это чуть больше чем 4, около 4 + 1/2. Но 2 в знаменателе не совсем точно; там должно быть число чуть больше чем 2, примерно 2 + 1/6. Таким образом, 415/93 примерно равняется 4 + 1/(2 + 1/6).
Но 6 в знаменателе не верно; настоящее значение чуть больше 6, 6+1/7. Таким образом, 415/93 является 4+1/(2+1/(6+1/7).
Это точное значение.
Опуская некоторые обязательные части в выражении 4 + 1 / (2 + 1 / (6 + 1 / 7)) мы получим краткую нотацию [4;2,6,7]. (Заметьте, что общепринято заменять только первую запятую точкой с запятой).
Представление как непрерывная дробь вещественного числа может быть определена таким образом. Она имеет несколько желательных свойств:
- Представление как непрерывная дробь конечно тогда и только тогда когда число является рациональным.
- Каждое рациональное число имеет по-существу единственное представление как непрерывная дробь. Каждое рациональное число можно представить в точности двумя способами, т.к. [a 0 ; a 1 , … a n − 1 , a n ] = [a 0 ; a 1 , … a n − 1 , a n − 1, 1]. Математики предпочитают иметь взаимно-однозначное соответствие между рациональными числами и цепными дробями; первая, более короткая нотация выбрана в качество каноническое представления.
- Представление как непрерывная дробь иррационального числа единственно.
- Цепная дробь является периодической тогда и только тогда, когда число является квадратичной иррациональностью, т.е. имеет форму
для целых a , b , c , d ; где b и d не ноль и c >1 и c не является точным квадратом.
К примеру, периодическая непрерывная дробь [1; 1, 1, 1, …] является золотым сечением, а периодическая непрерывная дробь [1; 2, 2, 2, …] является квадратным корнем из 2.
- Раннее усечение представления числа x в виде цепной дроби приводит к рациональному приближению x, которая в определенном смысле является «наилучшим» рациональным приближением.
Последнее свойство чрезвычайно важно. У десятичного представления числа его нет. Усечение десятичного представления числа приводит к рациональному приближению числа, но обычно к не очень хорошему приближению. К примеру, усечение 1/7 = 0.142857… в разных местах приводит к приближениям таким как 142/1000, 14/100 и 1/10. Но очевидно лучшим рациональным приближением будет само число «1/7». Обрывая десятичное представление π мы получаем приближения такие как 31415/10000 и 314/100. Цепная дробь π начинается [3; 7, 15, 1, 292, …]. Усекая это представление мы получаем отличные рациональные приближение 3, 22/7, 333/106, 355/113, 103993/33102, …. Знаменатели 314/100 и 333/106 почти одинаковые, но ошибка в приближении 314/100 в девятнадцать раз больше ошибки, чем в приближении 333/106. Как приближении π, [3; 7, 15, 1] более чем в сто раз точнее приближения 3,1416.
Данный реферат составлен на основе .
