Теория вероятностей — относительно молодая, но уже ставшая классической, ветвь математики. Развитие ее как отдельной науки пришлось на середину XVII века, и началось с переписки двух известных во всем мире французских математиков: Блеза Паскаля и Пьера де Ферма. Однако задачами, относящимися к просчету вероятностей в азартных играх, ученые начали интересоваться значительно раньше. Так, например, итальянский математик Лука Пачоли еще в 1494 в своем труде «Сумма <https://ru.wikipedia.org/wiki/%D0%A1%D1%83%D0%BC%D0%BC%D0%B0_(%D0%B6%D0%B0%D0%BD%D1%80)> арифметики, геометрии, отношений и пропорций» («Summa de arithmetica, geometria, proportioni et proportionalità»), рассмотрел одну из задач о вероятностях, но, к сожалению, привел ошибочное решение.
Сегодня методы теории вероятностей и математической статистики являются неотъемлемой частью практически любой дисциплины, как технической, так и гуманитарной направленности. Законы распределения случайных величин оказались применимыми не только к математике, физике, химии, и так далее, но и к дисциплинам, носящим отчасти прогностический характер, таким как социология, экономика, политология, etc.
В данной работе, познакомимся с основными понятиями, терминами и законами теории вероятностей и математической статистики, а так же с применением последних на практике.
1. СЛУЧАЙНАЯ ВЕЛИЧИНА
1.1 Определение случайной величины
Случайная величина — это фундаментальное понятие теории вероятностей и математической статистики.
Каждый автор по-своему формулирует понятие случайной величины. Е.С. Вентцель, например, определяет случайную величину, как величину, которая в результате опыта может принять то или иное значение, причем неизвестно заранее, какое именно [1].
Иначе говоря, случайная величина это величина, имеющая целый набор допустимых значений, но принимающая лишь одно, и какое именно, заранее точно сказать нельзя.
Формальное математическое определение случайной величины звучит следующим образом:
Пусть (Ω, F, P) — вероятностное пространство, тогда случайной величиной называют функцию X: Ω → R [2].
Случайную величину на практике обычно обозначают заглавными буквами, например: X, Y, Z, тогда, как возможные значения самой величины определяются строчными знаками: x, y, z.
случайный величина теория вероятность
Физические величины и единицы их измерения
... которые отождествлялись с названиями частей человеческого тела. ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ И ЕДИНИЦЫ ИХ ИЗМЕРЕНИЯ. Физические величины Технологическая деятельность человека связана с измерением различных физических величин. Физическая величина, Значение физической величины –, Измерением физической величины В основном в теории измерений принято пять типов шкал: названия, порядок, ...
1.2 Виды и примеры случайных величин
Различают два вида случайных величин: дискретные и непрерывные.
К дискретным относятся те случайные величины, множество значений которых конечно или фиксировано. Примером дискретной случайной величины, можно считать количество попаданий в цель при заранее определенном числе выстрелов.
Непрерывная случайная величина это такая величина, множество значений которой несчётно или бесконечно. В качестве примера для непрерывной случайной величины, можно взять количество кругов на воде, после попадания в нее камня, или расстояние, которое пролетит стрела, прежде чем упасть на землю.
Все случайные величины, ко всему прочему, имеют еще одну важную характеристику — ряд допустимых значений, который, в свою очередь, может как ограниченным, так и неограниченным. Отсюда, имеем, в зависимости от числа допустимых значений, ограниченные случайные величины, ряд допустимых значений конечен или фиксирован, и неограниченные, количество допустимых значений которых бесконечно.
Дискретные случайные величины могут иметь ограниченный и неограниченный ряд возможных значений, когда как непрерывные — только неограниченный.
На практике в теории вероятностей и математической статистике, как правило, имеют дело только с непрерывными случайными величинами.
ЗАКОНЫ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
2.1 Закон распределения дискретной случайной величины
Любое соотношение между допустимыми значениями случайной величины и вероятностями их наступления называют законом распределения дискретной случайной величины.
Существует два способа задания закона распределения:
- Аналитически, когда закон распределения задается в виде таблицы соответствия значений случайной величины и их вероятностью, именуемой рядом распределения:
Таблица 1 — ряд распределения случайной величины
|
… |
||||
|
… |
Здесь, в первой строке располагаются возможные значения случайной величины, а во второй — их вероятности, при этом сумма всех вероятностей равна единице:
![]() ; (1)
; (1)
- Графически, когда таблица распределения случайно величины принимает многоугольника распределения:
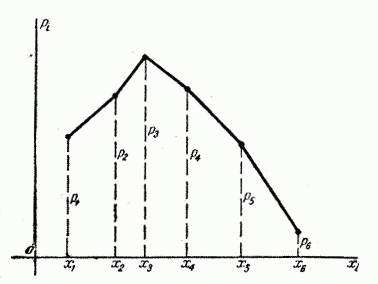
Рисунок 1 — многоугольник распределения случайной величины
Где сумма всех ординат многоугольника является вероятностью всех допустимых значений случайной величины, следовательно, также равна единице.
Существует также биномиальный закон распределения дискретной случайной величины или, второе название — закон распределения Бернулли.
Определение: дискретная случайная величина ξ распределена по биномиальному закону, если вероятность ![]() того, что событие A
того, что событие A ![]() наступит ровно m раз в серии из n испытаний по схеме Бернулли, равна:
наступит ровно m раз в серии из n испытаний по схеме Бернулли, равна:
![]() ; (2)
; (2)
Или в виде таблицы:
Таблица 2 — ряд биномиального распределения
|
m |
0 |
1 |
2 |
… |
|
|
|
|
|
… |
|
Примером является выборочный контроль качества производственных изделий, при котором отбор изделий для пробы производится по схеме случайной повторной выборки, т.е. когда проверенные изделия возвращаются в исходную партию. Тогда количество нестандартных изделий среди отобранных есть случайная величина с биномиальным законом распределения вероятностей.
Дискретная случайная величина называется распределенной по закону Пуассона, если она имеет неограниченное счетное множество допустимых значений 0, 1, 2, …, m, … Тогда соответствующие вероятности определяются формулой (3):
![]() , m = 0, 1, 2,…; (3)
, m = 0, 1, 2,…; (3)
Примером явления, распределенного по закону Пуассона, является последовательность радиоактивного распада частиц.
2.2 Законы распределения непрерывной случайной величины
случайный величина теория вероятность
Рассмотренные выше правила распределения случайной величины являются справедливыми лишь по отношению к дискретным величинам, в силу того, что все перечисленные законы строятся исключительно из соображения, что количество возможных значений случайной величины конечно и строго фиксировано. Именно поэтому, например, распределить непрерывную случайную величину по закону Пуассона или Бернулли не получится, так как невозможно перечислить количество допустимых значений данной величины — оно бесконечно.
Для описания распределения непрерывных случайных величин существуют следующие законы:
- Рассмотрим значения случайной величины Х такие, что Х<х. Вероятность события X<х зависит от x, т.е. является функцией x. Эта функция и называется интегральной функцией распределения и обозначается через F(x):
![]() ; (4)
; (4)
Равенство (4) читается:
Вероятность того, что случайное значение X находится левее значения х, определяется функцией распределения F(x).
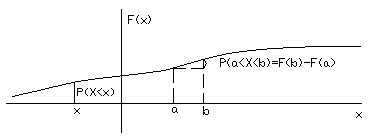
Рисунок 2 — Графическое представление функции распределения с.в.
Стоит отметить, что в виде функции распределения, можно описывать как непрерывную, так и дискретную случайные величины — это универсальная характеристика.
Для непрерывных случайных величин на практике, наравне с функцией распределения F(x), также принято использовать другой закон распределения — плотность распределения вероятностей случайной величины:
![]() ; (5)
; (5)
Равенство (5) — дифференциальный закон распределения случайной величины, который выражает крутизну функции распределения F(x).
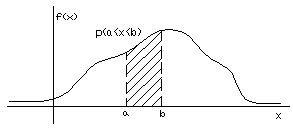
Рисунок 3 — Графическое представление дифференциального закона распределения с.в.
Заметим, что дифференциальный закон распределения случайной величины не является универсальным — он применим исключительно к непрерывным случайным величинам.
Одним из часто используемых на практике законов, является нормальный закон распределения — закон распределения Гаусса. Закон характеризует плотность вероятности нормально распределенной случайной величины X и имеет вид:
![]() , (6)
, (6)
Где a и σ параметры распределения имеют значения: ![]()
![]() .
.
Кривая распределения (рисунок 4а), или кривая Гаусса, получается симметричной относительной точки x = a — точки максимума. При уменьшении значения σ ордината точки максимума безгранично возрастает, кривая же при этом пропорционально расходится вдоль оси абсцисс, сохраняя площадь графика постоянной величиной, равной единице (рисунок 4б).
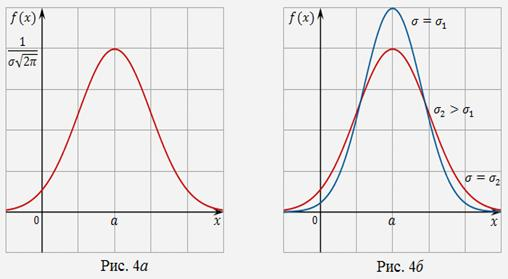
Рисунок 4 — Кривые распределения:
а — кривая Гаусса,
б — поведение кривой Гаусса при изменении параметра σ;
— На практике, нормальное распределение играет значимую роль во многих областях знаний, но особенное внимание ей уделяют в физике. Физическая величина подчиняется закону Гаусса, когда она подвергается влиянию большого числа случайных помех, что является крайне распространенной ситуацией, вследствие чего нормальное распределение чаще всего встречается в природе, и именно отсюда пошло ее название.
Непрерывная случайная величина называется равномерно распределенной на промежутке (a, b), если все ее возможные значения принадлежат этому промежутку и плотность распределения вероятностей постоянна — закон равномерного распределения непрерывной случайной величины, имеющий вид:
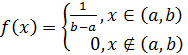 (7)
(7)
Для случайной величины Х, равномерно распределенной в интервале (a, b) (рисунок 5), вероятность попадания в любой интервал (x1, x2), лежащий внутри интервала (a, b), равна:
![]() ; (8)
; (8)
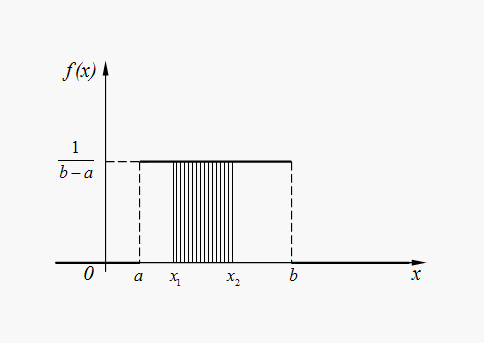
Рисунок 5 — График плотности равномерного распределения
В качестве примера равномерно распределенных величин, можно взять ошибки округления. Так, если все табличные значения некоторой функции округлены до одного и того же разряда ![]() , то выбирая наугад табличное значение, мы считаем, что ошибка округления выбранного числа — случайная величина, равномерно распределенная в интервале
, то выбирая наугад табличное значение, мы считаем, что ошибка округления выбранного числа — случайная величина, равномерно распределенная в интервале ![]() , где
, где ![]() .
.
Непрерывная случайная величина X называется показательно распределенной, если плотность распределения ее вероятностей имеет вид:
![]() ; (9)
; (9)
В качестве примера, возьмем время Т безотказной работы компьютерной системы, где Т — случайная величина, имеющая показательное распределение с параметром λ, физический смысл которого — среднее число отказов в единицу времени, не считая простоев системы для ремонта.
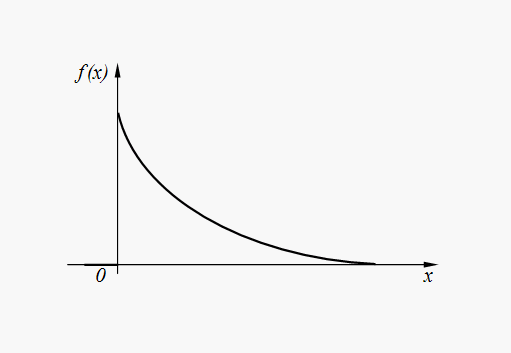
Рисунок 6 — График плотности показательного распределения
ЗАКЛЮЧЕНИЕ
Методы, средства и законы теории вероятностей и математической статистики на протяжении всех этапов формирования дисциплины, являлись актуальным, какими и остаются вплоть до наших дней. Главный принцип методов, позволивший затронуть столь огромное количество отраслей и сфер знания — универсальность. Их с легкостью можно применять в любой дисциплине, и при этом они не теряют своей силы, остаются справедливыми.
Но никогда еще теория вероятностей не была столь востребована, как сегодня. Связано это в первую очередь с невероятными темпами развития и роста вычислительной техники. С каждым годом она становится все сложнее, повышается быстродействие, количество производимых в секунду операций, и все это происходит не без участия математической статистики, которая, в свою помогает оптимизировать работу вычислительных систем и комплексов, повышает точность расчетов, осуществляет прогностическую функцию.
Данная работа частично помогает разобраться в азах дисциплины. Знакомит с фундаментальными понятиями, такими как дискретные и непрерывные случайные величины, поясняет разницу между последними. Знакомит с законами их распределения, с дальнейшим применением всех полученных знаний на практике.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
[Электронный ресурс]//URL: https://drprom.ru/referat/nepreryivnyie-sluchaynyie-velichinyi/
1. Вентцель, Е.С. Теория вероятностей/ Е.С. Вентцель — М.:Наука, 1969г.
— Смирнов, Н.В. Курс теории вероятностей и математической статистики для технических приложений./ Н.В. Смирнов, И.В. Дунин-Барковский — М.: «Наука», 1969г.
— Пустыльник, Е.И. Статистические методы анализа и обработка наблюдений: учебное пособие/ Е.И. Пустыльник. — М.:«Наука», 1968г.
— Джонсон, Н. Статистика и планирование в науке и технике./ Н. Джонсон, Ф. Лион — М.: «Мир», 1969г.
-http://www.wikipedia.org/
Аннотация
Загоскин Я.С. «Что такое случайная величина?»
Челябинск: Юургу
Пс-236,15 с.
Библиогр. Список — 5 наим.
Цель реферата: Познакомиться с базовыми терминами теории вероятностей и математической статистики.
Задачи реферата: Разобраться с понятием случайной величины.
Рассмотрено понятие случайной величины, определена классификация случайных величин, рассмотрены законы их распределения, примеры применения законов и методов на практике, а также проанализирована перспективность дисциплины.
