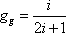Позначимо через nk число часток, що знаходяться в k-тому квантовому стані (це так звані числа заповнення різних квантових станів) і поставимо задачу обчислити середні значення nk цих чисел, причому будемо розглядати випадок, коли nk < <1
Тобто ми розглядаємо досить розріджений газ. (Фактично це виконується для всіх звичайних молекулярних чи атомних газів).
Умова nk << 1 означає, що в кожен момент часу в кожному квантовому стані реально перебуває не більше однієї частинки, у зв’язку з цим можна нехтувати не тільки безпосереднім силовим взаємодією частинок, але і їх непрямим квантомеханические взаємним впливом. А ця обставина, в свою чергу, дозволяє нам застосувати до окремих молекулам формулу розподілу Гіббса.
Отже, застосувавши до молекул формулу Гіббса, ми стверджуємо, що:
, де a — константа, що визначається з умови нормування:
(N — повне число частинок в газі).
Це і є розподіл Больцмана (L.Boltzmann, 1877).
Константа a може також бути виражена через термодинамічні величини газу.
Застосуємо розподіл Гіббса до сукупності всіх часток, що знаходяться в даному квантовому стані. Ми можемо це зробити (навіть якщо nk НЕ малі), оскільки безпосереднього силового взаємодії між цими та іншими частинками немає, а квантомеханические ефекти мають місце лише для часток, що знаходяться в одному і тому ж стані. Покладемо в загальній формі розподілу Гіббса з перемінним числом частинок E = nk e k, N = nk і, приписуючи індекс k величиною W, отримаємо розподіл ймовірностей різних значень nk у вигляді:
Зокрема, є ймовірність повної відсутності частки в даному стані. У нас цікавить випадку, коли nk << 1, ймовірність w0 близька до одиниці; тому у виразі w1 для ймовірності наявності однієї частинки в k-тому стані можна покласти, опускаючи члени вищого порядку малості, exp (Wk / T) = 1. Тоді
Що ж до вірогідності значень nk> 1, то вони в цьому наближенні повинні бути покладені рівними нулю. Тому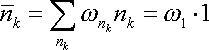 
І ми отримуємо розподіл Больцмана у вигляді: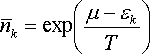 
Таким чином, коефіцієнт a в законі розподілу Больцмана виявляється вираженим через хімічний потенціал газу.
Електричний струм
... частинок під дією електричного поля. До заряджених частинок відносяться електрони, іони, протони. Оскільки протони знаходяться в ядрі атома, то вони ніякої ролі не можуть мати в процесі передачі електричного струму. ... позитивними іонами решітки. Іони решітки перебувають при цьому в коливальному стані. Під час проходження струму дрейфуючі електрони , стикаючись з іонами, віддають набуту від ...
Вільна енергія больцманівського ідеального газу
Застосуємо загальну формулу:
для обчислення вільної енергії газу, описуваного статистикою Больцмана:
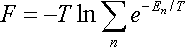
Написавши енергію En у вигляді суми енергій
всім станам газу до підсумовування по всіх станах окремої молекули. Кожне стан газу визначатиметься набором N (число молекул в газі) значень ek, які в больцманівського випадку можна вважати різними між собою (в кожному молекулярному стані — не більше однієї молекули).
Напишемо exp (-En / T) у вигляді добутку множників exp (-ek / T) для кожної з молекул і підсумовуючи незалежно по всіх станах кожної молекули, ми отримаємо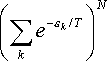 
Набір можливих значень ek для всіх молекул газу однаковий, а тому однакові і суми
S exp (-ek / T).
Врахуємо, однак, що всі набори N різних значень ek, що відрізняються лише розподілом однакових молекул газу за рівнями ek відповідають одному й тому ж квантовому станом газу. В статсумме ж кожне з станів повинно враховуватися один раз. Тому ми повинні ще розділити вираз (*) на число можливих перестановок N молекул один з одним, тобто на N !.
Таким чином: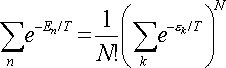 
Підставляючи в загальну формулу, отримуємо:
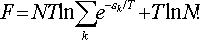
Оскільки N — дуже велике число, то для ln (N!) можна скористатися наближенням ln (N!) » N ? ln (N / e).
В результаті
отримаємо наступне: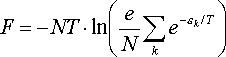 
Ця формула дозволяє нам обчислити вільну енергію будь-якого газу, що складається з однакових частинок і підкоряється статистиці Больцмана.
У класичній статистиці це може бути переписано як:
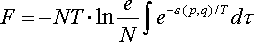
Дво-і трьохатомної газ. Обертання молекул.
Двохатомні молекули з однакових атомів володіють специфічними особливостями, які ми розглянемо на прикладі пара-і ортоводорода.
Параводорода
Законы идеальных газов
... стенки. Вместо сил, действующих на налетающие молекулы, можно по третьему закону Ньютона ввести равные молекулы пристеночного слоя. Пусть P- средняя сила давления газа на стенку, а средняя сила, ... с которой молекулы пристеночного слоя втягиваются внутрь газа. Тогда идеальный газ ...
Як вже було розглянуто, загальна статсумма виражається як
«Обертальна» і «коливальна» суми тут визначаються як
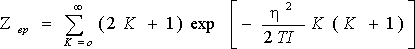
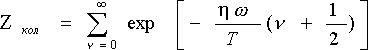
Множник (2К + 1) під обертальної сумі враховує виродження обертальних рівнів за напрямками моменту К. Вільна енергія, зрештою виражається з трьох частин:
Перший член пов’язаний зі ступенями свободи поступального руху молекул, назвемо його поступальної частиною.
Обертальна і коливальні частини: 
Поступальна частина завжди виражається формулою типу
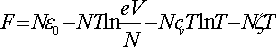, з постійною теплоємністю і хімічної постійної 
.
Повна теплоємність буде виражатися у вигляді суми, 
.
Займемося обертальної вільної енергією. Якщо температура настільки велика, що 
, то обертальна статсумма може бути замінена інтегралом
Тут e (M) — вираз кінетичної енергії обертання як функції моменту обертання М.
Звідси вільна енергія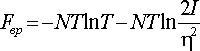 
Таким чином, при розглянутих не дуже низьких температурах обертальна частина теплоємності виявляється постійною і рівною відповідно до загальними результатами класичного розгляду. Обертальна частина хімічної постійної дорівнює 
. Існує значна область температур, в якій виконується і в той же час коливальна частина вільної енергії, а разом з нею і коливальна частина теплоємності відсутні. У цій області теплоємність двухатомного газу дорівнює, тобто 
,, А хімічна постійна 
.
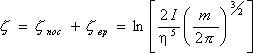У граничному випадку низьких температур 
достатньо зберегти два
перших члена суми: 
М язи як частина опорно-рухової системи
... необхідне для підтримання сталої температури тіла. Робота м’язів супроводжується витратами енергії. Енергія для скорочення м’язів утворюється при ... АТФ. При ферментативному відщепленні від АТФ однієї молекули фосфорної кислоти утворюється АДФ і виділяється енергія. ... до іншої кістки - хвостом, між ними потовщена частина – його тіло або черевце. За формою м’язи поділяються ... тулоба. Грудна клітка. М’
У тому ж наближенні для вільної енергії:
Ентропія:
І, нарешті, теплоємність: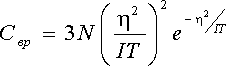 
двоатомний газ з молекулами з
однакових атомів. Обертання молекул.
Двохатомні молекули, що складаються з однакових атомів, володіють специфічними особливостями, що призводить до необхідності змінити отримані вище формули.
Перш за все, зупинимося на високотемпературному випадку в класичному розгляді. Завдяки тому, що ядра однакові, дві взаємно протилежні орієнтації осі молекули відповідають тепер одному і тому ж фізичному стану молекули. Тому класичний статистичний інтеграл (**) повинен бути розділений навпіл, і приведе до зміни хімічної постійної, яка тепер дорівнює 
.
Зникне також і множник 2 в аргументі логарифма (***).
Фактично це питання нас цікавить в застосуванні до изотопам водню (і 
), і нижче всюди будемо мати на увазі саме ці гази. Вимога квантовомеханічною симетрії по ядрам призводить до того, що у електронного терма (нормальний терм молекули водню) обертальні рівні з парними і непарними значеннями К володіють різними ядерними кратностями виродження: рівні з парними (непарними) К здійснюються лише при парному (непарному) сумарному спині обох ядер і мають відносні кратності виродження
