«Моделирование текстовых задач в начальной школе по УМК «Школа России»». Цель

метки: Моделирование, Задача, Решение, Работа, Класс, Конструирование, Математик, Помощь

В начальных классах программу по математике включены различные виды задач. Чтобы сделать урок математики интересным для детей, нужно включить в уроки занимательных заданий, сказочных героев, игровые ситуации. Для развития интереса к математике, логического мышления у младших школьников при решении текстовых задач надо применять метод моделирования.

Проблема : как, используя традиционный УМК по математике (программа М. И Моро, М .А. Бантовой, Т .В. Бельтюковой), анализировать задачу более продуктивно, чтобы она из просто арифметической превратилась в развивающую? Можно ли научить самостоятельно решать задачи каждого ученика?

Изучив теоретические подходы к обучению решать задачи, а также разнообразные практические приемы, пришли к выводу, что можно.

Для каждого ученика главное — понять задачу, т.е. выяснить, о чем эта задача, что в ней известно, что нужно узнать, как связаны между собой данные, каковы отношения между данными и искомыми параметрами. Применяя моделирование задачи можно учить этому детей.

Мы взяли курсовую работу на тему: «Моделирование текстовых задач в начальной школе по УМК «Школа России»».

Цель : теоретически обосновать и практически проверить эффективность использования моделирования в процессе обучения решению задач в начальной школе.

Объект исследования, Предмет исследования

Гипотеза: если при обучении решению задач использовать моделирование, то это способствует формированию умения решать задачи.

Задачи :

-разработать методические рекомендации по использованию разных моделей;

-накопление дидактического материала, используемого как для всего класса, так и для индивидуальной работы учащихся;

Решение задач с использованием системы MathCAD и Scilab

... операционной системы. В данной курсовой работе требуется проанализировать как влияет изменение параметров на электрическую цепь второго порядка используя системы компьютерной математики(СКМ) - MathCad и Scilab , которые являются отличным примером системы компьютерного моделирования. ...

Методическая основа исследования

Изучение роли текстовых задач в обучении и воспитании издавна занимало видно место в исследованиях, посвященных методике обучения математике младших школьников. Это нашло отражение и развитие в работах многих современных методистов (Н. И. Моро, К. И. Нешков, А С. Пчелко, А.М. Пышкало, В.Н. Рудницкая, Л. Н. Скаткин, Е. Н .Тальянова, П. М. Эрдниев и др) и психологов (Н ,А Менчинская, Л, М, Фридман и другие)[1,с.3].

Курс обучения младших школьников математике по программе М. И. Моро предполагает формирование у них ряда представлений и понятий, ознакомление учащихся с теоретическими фактами, формирование умений и отработку соответствующих умений и навыков применения теоретических знаний в решении задач и других математических операций[2,с.3]. Задачей школьного курса математики является — научить применять теоретические знания на практике и уметь самостоятельно находить пути решения предполагаемых программой задач и уметь применять общие подходы к их решению.

В.Н.Рудницкая в программе по математике для начальной школы важнейшей целью определяет создание благоприятных условий для полноценного интеллектуального развития ребенка на уровне, соответствующем его возрастным особенностям и возможностям, и обеспечение необходимой и достаточной математической подготовки ученика для дальнейшего обучения[3,с.4]

В ряде исследований(Л,М,Фридман,Г.Т.Зайцев,М.А.Бантова,Т.В.Бельтюкова) была предпринята попытка создать классификацию текстовых задач, т.к. по мнению исследователей ,это позволило бы выявить особенности методики обучения решению задач каждого типа. Л.М Фридманом на основе созданной им общей теории задач была предпринята попытка разработки логико-математической теории сюжетных задач. В основе программы Н.Б. Истоминой лежит методическая концепция, необходимость целенаправленной и систематической работы по формированию у младших школьников приемов умственной деятельности: анализа и синтеза, сравнения, классификации, аналогии и обобщения, в процессе усвоения математического содержания[3,с.4].

Теоретическая основа исследования, Методы исследования:

-теоретический анализ методической литературы:

-экспериментальные методы:

-методы изучения продуктов деятельности:

-методы статической обработки данных

База исследования, Этапы исследования

На первом этапе изучалась, и анализировалось психолого-педагогическая и методическая литература: на основе полученной информации была определена тема исследования, выдвинута гипотеза, определены объекты и предмет, цель и задачи исследования, намечена программа исследовательской работы. Была проведена вводная диагностика для определения сформированности у младших щкольников умения решать задачи.

На втором этапе проводился формирующий эксперимент, направленный на развитие умения решать текстовые задачи младшими школьниками на уроках математики на основе моделирования.

Филипас 1. Термодинамическое исследование скважин

... пласта для определения его параметров. Эти исследования также можно применять и для изучения газовых скважин. 1. Термодинамическое исследование скважин. Известно, что колебания температуры на земной ... геотерма. Термограмма - распределение температуры в работающей скважине имеет отклонения от геотермы, которые связаны с термодинамическими и гидродинамическими процессами, происходящими в продуктивном ...

На заключительном этапе была проведена письменная контрольная работа, по результатам который был сделан вывод об уровне сформированности умения решать задачи, о степени подтверждения гипотезы. Разработали некоторые методологические рекомендации.

Теоретическое значение, Практическая значимость, Апробация работы

Материал исследования по мере их получения использовались в практике собственной работы в качестве учителя 2 класса МОБУ СОШ с. Ассы.

Структура и объем работы

Курсовая работа состоит из введения, 2 глав, заключения, список используемой литературы и приложений.

Глава I . Теоретико-методологическое основание моделирования в системе начального образования

1.1Моделирование как один из методических приёмов обучения решению текстовых задач в начальной школе

Одна из главных обязанностей начальной школы — научить детей решать текстовые арифметические задачи. Решение задач способствует развитию логического мышления, математической речи, воображения, практических умений и навыков. В начальных классах математики много текстовых задач, понятие задача используется тогда, когда идет речь об арифметических задачах, сформулированных в виде текста. Такие задачи называются «текстовыми».[5.с. 6 ]

Текстовая задача – это словесная модель некоторого явления (ситуации процесса), чтобы решить такую задачу, надо перевести её на язык математических действий, т.е. построить её математическую модель. При помощи моделирования можно осуществить изучение сложного на основе простого, незнакомое с опорой на знакомое, то есть сделать мир доступным для подробного изучения. Для чего же младшим школьникам нужно овладеть приемами моделирования?

Во-первых, введение в процесс обучения модели и моделирования меняется отношение учащихся к учебному предмету, делает их познавательную деятельность осмысленной и продуктивный.

Во-вторых, целенаправленное обучение методу моделирования приближает младших школьников к методам научного познания, обеспечивая их умственное развитие. Чтобы вооружить учащихся навыками моделирования необходимо, чтобы школьники сами строили модели, самостоятельно изучали какие-либо объекты или явления при помощи моделирования.

В состав учебного моделирования входят следующие пункты или уровни:

• предшествующий анализ текста задачи;

-перевод текста на знаково-символический язык, который может осуществляться вещественными или графическими средствами;

• построение модели;
• работа с моделью
• соотнесение данных, полученных с использованием модели, с реальностью или с текстом.

Каждый элемент активности на уровне моделирования имеет конкретное содержание с определенным составом операций и средств.

Конструирование и моделирование деревянной мебели на примере ...

... изделий. Объектом работы является процесс конструирования и моделирования мебели из древесины. Предметом курсовой работы являются конкретные мебельные изделия, созданные из древесины с применением процессов моделирования и конструирования. Выпуск таких товаров постоянно возрастает. Можно выделить следующие виды производств изделий из древесины: ...

Предварительный анализ содержания текста задачи включает несколько приемов. Он предполагает работу над отдельными словами, терминами, перефразирование и переформулировку текста. Другим способом анализа текста, ведущего к пониманию его смысла, становится постановка вопросов, определенной порядок чтения текста, выделение основных смысловых пунктов текста. В общей деятельности моделирования действие анализа текста является подготовленным этапом для построения модели. Перевод текста на знаково-символический язык делает понятными связи и отношения, скрытые в тексте, и помогает тем самым поиску и нахождению решения.

[ 20.с.7 ]

Моделирование производится для того чтобы получить данные о реальности в прозрачной форме. Из практики известно, что учащиеся после решения задачи проверяют свои ответы с целью убедиться в том, что они удовлетворяют условия и требования задачи. Принципиально важным при этом является не столько выявление правильности, сколько сравнение данных полученных на модели с ее описанием в тексте.

При создание различного рода моделей , очень важно установить какая информация должна быть введена в модель, какие средства (символы знаки) будут применяться для каждой выделенной составляющий текста, какие из них должны иметь постоянную символику, а какие – различную. Применение одним и тех же знаково-символических средств, при построении модели для задач с разнообразными сюжетами и различных типов способствует развитию общего порядка анализа задачи, выделению составляющих ее компонентов и нахождению методов решения.[ 20.с.7 ]

Для того, чтобы решить задачу, ученик учится переходить от текста (словесной формы) к представлению ситуации (мысленной модели), а от ее — к записи решения при помощи математических знаков (знаково-символический модели), все эти модели являются воспроизведением одного и того же объекта — содержания задачи. Они различаются друг от друга только тем, что исполнены на различных языках слов (словесная модель); языке образцов (мысленная), языке математических знаков (знаково — символическая).

Ученикам с неодинаковым уровнем развития мыслительной деятельности требуется различные приемы работы с задачей, поэтому на уроках математики необходимо знакомить детей с несколькими видами моделей к одной и той же текстовой задаче. Это требуется для того, чтобы дети не оказались в ситуации неуспеха, а чувствовали себя способными разрешить любую задачу.[20.с.8]

1.2 Виды моделирования и методика решения текстовых задач, Вспомогательная модель

Рисунок. Все ученики младших классов любят рисовать, с нетерпением ждут уроки рисования. Знакомство с этой моделью начинаю в 1 классе.

Во-первых, рисование — любимый вид деятельности малышей, во-вторых, приём хорош для развития моторики рук, в-третьих, рисование является развивающим упражнением. Детей с этой моделью знакомят с 1 класса. Рисунки бывают предметные (например, ложки), сюжетные (например, лошади) и схематичные.

Краткая запись. С этой моделью начинаем работать в конце 1-го класса., Введение краткой записи параллельно с рисунком получится удачным.[3.с.8], Например:, Было 3 шара (показываю и повешу 3 шара)., Назиле подарили еще 1 шарик (показываю)., У Назили всего сколько шариков?

Таблица . Знакомлю с этой моделью в конце 1-го, начале 2-го класса.

Построение математических моделей при решении задач оптимизации

... решаются средствами элементарной математики. Следует различать также два вида задач на оптимизацию. В задачах первого вида улучшение достигается за счет коренных качественных изменений: выбор новых конструктивных решений, переход на ...

Бул ғ ан ( билдәле)

Алгандар (

Сумма

Или другая таблица

Хакы

Миҡдары

Сумма

Чертёж. Применяем тогда, когда числовые данные в задаче удобные, позволяющие начертить отрезок заданной длины. Этот вид модели особенно нравится мальчишкам, они с удовольствием чертят отрезки и находят ответы задач.

Пример. « Когда веревку длиной 2 метра удлинили на несколько метров, то получилась веревка длиной 5 метров. На сколько метров удлинили веревку?»

Этапы работы., Какой длины была сначала веревка? (2 м), Какой длины вычерчиваем первый отрезок? (2см), Что произошла с веревкой? (Увеличивалась на несколько метров.), Как изменится отрезок? ( Увеличится на несколько сантиметров.), Какой длины стала веревка?(5м), Какой длины станет наш отрезок?(5см), Отметим на чертеже, насколько увеличился наш отрезок., Что нужно узнать в задаче?, Как на нашей модели отмечено искомое?

/_____/_____/ 2см

/_____/______ /______/_____/______/ 5см

?

Далее выбирается арифметическое действие., Пример. «

Чертёж имеет такой вид.

Камилдың /_____/

Алмазды ң /_____/______/______/ ?

Или

Камилды ң /__1м___/

Алмазды ң /___1м____/_1м____/ ?

Схема. Знакомим в начале 2-го класса. Подбор задач в этом классе позволяет применять эту модель на материале обратных задач, при решении задач разными способами.

Пример: «

/__________10________________/

/___________7________/ ?

Блок-схема (разбор задачи аналитическим способом, то есть с вопроса).

Изучение этой модели возможно уже в конце 2-го класса, когда все предыдущие модели изучены хорошо, широко и системно используются на уроке.[3.с.10]

1.3.Методика работы с моделями.

На уроках математики, при решении задач, ученики должны использовать разные методы моделирования. Для этого надо вести подготовительные работы (упражнения).

Эти упражнения целесообразно проводить с начала обучения решению задач:

-развитие графических навыков учащихся, то есть отработку умений пользоваться линейкой и карандашом,

• чертить прямые линии, отрезки, ставить точки, чертить равные отрезки;

— развитие зрительного восприятия, то есть совершенствование у учащихся умения определять длину отрезка, сравнивать отрезки на глаз;

-развитие мышления, потому что для выполнения любого, даже элементарного, действия (например, соединить две точки отрезком) требуется включение мышления.[ 12.с.11]

Дальше обучаем учащихся решать задачи с помощью моделирования. Процесс ведется от простого к сложн

Последняя работа направлена на отработку умения решать задачи с помощью моделирования, и включает различные задания на преобразование задач, на обучение учащихся самостоятельному составлению задач, сравнение задач, выбор соответствующей модели к задаче [17.с.11]

Контрольная работа: Архитектурные решения одноэтажного дома

... и конструктивные решения жилых малоэтажных зданий. Задачи работы – дать характеристики типов объемно-планировочных решений одноэтажных жилых зданий, дать характеристику конструктивной стороны одноэтажной застройки в плане соответствия планировочных решений и типов домов наиболее ...

Обучение решению текстовых задач с помощью моделирования необходимо начинать тогда, когда учащиеся научатся четко и аккуратно выполнять графические построения (ставить точки, строить отрезки).

Для формирования этих умений мы предлагаем следующие задания:

• Поставь в тетради две точки, проведи через них прямую линию.
• Поставь в тетради точку.

Проведи через нее прямую линию. Проведи еще одну прямую линию.

• Поставь две точки на листе бумаги. Согни лист бумаги так, чтобы точки лежали на линии сгиба.
• Нарисуй две ленты: одну ленту длиной 3 см и шириной 1 см, вторую длиной 5 см и шириной 1 см.
• Нарисуй три квадрата и два треугольника. Обведи их кривой замкнутой линией.

-Начерти один под другим три отрезка так, чтобы первый отрезок был длиннее двух других, а третий — короче двух других.

• Начерти отрезок. Поставь:

Точку А ближе к началу отрезка;

точку В ближе к середине отрезка;

• точку С ближе к концу отрезка.
• Начерти отрезок длиной 10 см, раздели его на пять равных частей.
• Начерти отрезок. Поставь точку К ближе к концу отрезка.
• Соедини дугой:
• начало отрезка и точку К (дугу проводим над отрезком);
• точку К и конец отрезка (дугу проводим над отрезком);
• начало и конец отрезка (дугу проводим под отрезком).[ 16.с.12]

После этих работ, мы предлагаем упражнения, которые подготавливают учащихся к решению задач с помощью моделирования.

1. На столе лежали 3 книги, потом положили еще 2. Закрась красным цветом книги, которые доложили.

2.У Руслана – 1 ручка фиолетового цвета и 3ручки синего цвета. Закрась столько квадратиков, сколько ручек у Руслана.

3.В одном наборе 6 карандашей, а в другом на 3 больше. Обозначь каждый карандаш кругом и закрась карандаши второго набора.

Обведи на каждой схеме красным цветом отрезок, который соответствует данному выражению.

4.Вилка длиннее ложки на 2 см. Отметь на схеме отрезок, который обозначает 2 см.

5.У Каримы 3 конфеты, у Марьям— 5, а у Лилии на 4 конфеты больше, чем у Каримы. Закрась синим цветом конфеты каждой девочки, если каждая конфета обозначена квадратом.

В дальнейшим закрепляем умение учащихся решать задачи с помощью моделирования.

1.На одной полке 15 книг, на второй на 4 книги больше, чем на первой., Поставь вопрос к условию задачи и реши ее, используя схему.

2. На сколько больше ящиков огурцов привезли в первый магазин, чем во второй?, Составь условие по данному вопросу и реши задачу с помощью схемы.

3.В коробке 9 мячей. Из них 3 красных, а остальные зеленые. Сколько зеленых мячей в коробке? Выбери соответствующую схему и реши задачу.

Прежде чем решать задачу ребенок должен запомнить ее, понять, о чем идет речь в задаче. Для этого задача прочитывается один-два раза про себя, затем вслух детьми, если дети читают хорошо, или учителем. Далее, в случае необходимости, проводится словарная работа (разъяснение смысла терминов, используемых в задаче), описание жизненных ситуации, которая рассматривается в задаче. Далее задачу можно разбить на смысловые ситуации. Затем задача повторяется вслух и одновременно, если это необходимо, иллюстрируется краткой записью или другим удобным способом. Иногда дети описывают ситуацию, которая происходит в задаче своими словами, как они ее понимают (словесная картина).[10.с.]

Курсовая работа пятиэтажный жилой дом

... назначения начинают с решения вопросов конструирования - выбора конструктивной и строительной системы здания… 1. Характеристика здания Мною запроектирован жилой шестиэтажный кирпичный дом. Конструктивная система ... СНБ 2.02.01-98 здание относится II степени. Класс ответственности здания по СНиП2.01.07-85 IIкласс. Планировочное решение здания : односекционное. В здании запроектировано техническое ...

Рассмотрим это на примере., Задача. Когда с полки сняли 2 книги, там осталось 4. Сколько книг лежало на полке сначала?

• Сколько книг осталось на полке? 4

Изобразим.

• Раньше книг было больше или меньше? Почему?
• Больше. Здесь нет книг, которые сняли с полки.
• Знаем ли мы, сколько книг было сначала? Нет.

Покажем это на чертеже и поставим вопросительный знак.

?

• Почему книг стало меньше?
• С полки сняли две книги.

Изобразим две книги внизу, под скобкой.

____________________________________

?

• Как узнать сколько книг было на полке?

Нужно сложить книги, которые остались на полке, и те, которые сняли.

Вывод по главе

Действующие программы по математике требуют развития у детей самостоятельности в решении текстовых задач. Каждый выпускник начальной школы должен уметь кратко записывать условия задачи, иллюстрируя ее с помощью рисунка, схемы или чертежа, обосновывать каждый шаг в анализе задачи и ее решении, проверять правильность решения.[5.с.15]

Согласно программе работа над текстовыми задачами в начальной школе занимает почти половину всего времени. Задачи выступает и целью обучения и способом обучения математике. Они являются средством развития логического мышления, помогают использовать полученные знания на практике.

На уроках математики с детьми всегда ведется индивидуальная и групповая работа, так как логическое мышление не у всех хорошо развито. Многие дети не умеют самостоятельно решать задачи, а надо этому их учить, начиная с первого класса. При решении задач каждый ученик должен понять задачу, то есть знать, что в ней известно, что нужно узнать, как связаны между собой данные, каковы отношения между данными и искомыми параметрами. Для этого следует применять моделирование и учить этому детей.

Использование моделирования на уроках математики в начальных классах позволяет ускорить формирование у младших школьников умений и навыков выполнять различные практические упражнения; повышает у детей интерес к изучению математики, что способствует успешности выполнения всей учебной работы.

Рисунки, схемы, чертежи помогают учащимся сознательно искать наиболее рациональные пути решения задач.

Графические изображения, используемые для постановки познавательных задач, помогают ученикам найти проблемные ситуации, а затем и найти возможный путь решения.[6.с.15]

Глава II . Экспериментальная работа по моделированию содержания текстовых задач

2.1 Описание опыта работы над текстовыми задачами по УМК «Школа России».

В математике УМК «Школа России» ученики с простыми задачами знакомятся в 1-ом классе при изучении чисел первого десятка. Это — задачи на сложение и вычитание. Во 2-ом классе ученики изучают действие деление и умножение чисел и знакомятся с новыми задачами, при решении которых используется эти действия. В 3-eм классе ведется работа по закреплению умений решать задачи в одно, два или три действия; происходит знакомство с задачами на нахождение доли числа; решаются задачи с величинами: цена, количество, стоимость. В 4-ом классе изучают более сложные задачи, которые связаны величинами, например, скоростью, временем и расстоянием.

Pscad моделирование ветрогенератора

... предлагает лучшую альтер нативу прямым измерениям. Целью этой работы является изучение аэродинамики горизонтального ветрогенератора путем численного решения управляющих уравнений с использованием метода конечных объемов ... -прежнему основаны на BEM [4, 51 и 52]. Аэродинамическое моделирование роторов горизонтального ветрогенератора с помощью обычных инженерных методов достигло точки, в которой нельзя ...

В первом классе детей надо учить анализировать и составлять плана решения задачи, так как у них не одинаковый уровень развития мыслительной деятельности. Многие из них не умеют словесную модель перевести на язык математических действий. Все дети этого возраста, после ознакомления с содержанием задачи, сразу же спешат назвать ответ, и только по требованию учителя сообщают решение задачи. Ошибки допускают не все, потому что сюжеты задач близки жизненному опыту детей и числа в условии небольшие. Ответ можно найти даже по представлению, не прибегая к вычислениям. Решение задач кажется первокласснику совсем не сложным. Постепенно формируется прочная привычка сводить всю работу над задачей к простой вычислительной деятельности. Но процесс решения любой текстовой задачи состоит из нескольких этапов:

Восприятие и первичный анализ задачи., Поиск решения и составление плана решения., Выполнение решения и получение ответа на вопрос задачи., Проверка решения., Мы выделяли следующие возможные приёмы выполнения первого этапа решения текстовой задачи:

1. Разный способ анализа задачи – с вопроса или от данных к вопросу.

2. Представление жизненной ситуации, которая описана в задаче.

3. Разбиение текста задачи на смысловые части. Применение этого приёма обеспечивает как понимание содержания задачи, так и запоминание.

4. Переформулировка текста задачи, т.е. «отбрасывание» ненужных деталей, уточнение и раскрытие смысла задачи.

5. Моделирование ситуации, описанной в задаче (т.е. краткая запись), с помощью:

а) реальных предметов, о которых идёт речь в задаче;

• б) предметных моделей;
• в) опорных слов;
• г) графических моделей в виде рисунка;
• схемы;

• д) чертежа;
• е) таблицы;

На более поздних этапах обучения использую следующие формы работы:

6. Анализ задач с недостающими или лишними данными.

7. Составление условия к данному вопросу.

8. Постановка вопроса к данному условию[12.с.18].

Некоторые

Работы: Моделирование динамических процессов фильтрации для горизонтальных ...

... перерастает в следующий режим - это псевдорадиальный режим течения. Понятие о радиальном режиме течения в пласте является основополагающим для теории гидродинамических исследований. Этот режим предполагает, ... С, Симонов М.В. Повышение информативности ГДИС горизонтальных скважин методом моделирование точечных источников // VII Научно-техническая конференция молодых ученых ООО «ГазпромНефть НТЦ», - ...

а) реальные предметы, о которых идёт речь в задаче;

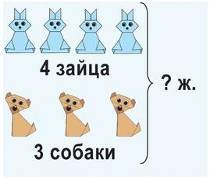
б) предметные модели;

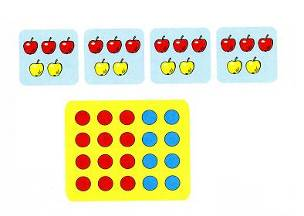
в) опорные слова;

М әрйәм – 7 шар

Та ңһылыу – 2 шарға күберәк-?

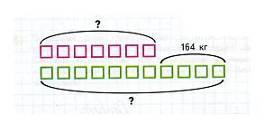
г) графические модели в виде рисунка и схемы;

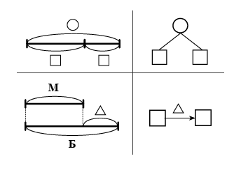
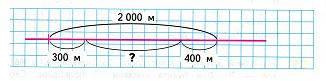
д) чертежи;

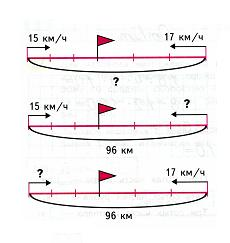
е) таблицы;

Приведу пример работы над условием с недостающими данными или заменой условия (вопроса).

Пеналда

Өҫтәлдә ҡәләмдәр һаны пеналдағына ҡарағанда 4-кә күберәк

— Предлагаю учащимся данные, которыми можно дополнить условие задачи, чтобы ответить на ее вопрос. Среди них есть и неверные.

В пенале 7 карандашей., В пенале на 6 карандашей больше., На столе 9 карандашей., Всего в пенале и на столе 14 карандашей.

2.2. Содержание и этапы опытно-экспериментальной работы.

В настоящий момент учащиеся чаще всего допускают ошибки при выборе формул для решения задач, поэтому всегда используют разнообразные приемы моделирования процессов (предметные картинки, составление схем, таблиц диаграмм).

Оформление решения задачи в виде выражения в некоторых частях вызывает затруднения у учащихся. Свою практику я проходила МОБУ СОШ с.Ассы Белорецкого района.

Были взяты два класса: 2бкласс-экспериментальный и 2а класс-контрольный. Данные классы по уровню развития примерно одинаковые.

Для эксперимента была выбрана тема «Решение текстовых задач»., Задачи практической работы:

• подобрать задания для проверочной работы:
• провести письменную работу по решению задач:
• проанализировать допущенные ошибки:
• апробировать систему задач с использованием моделей:
• провести контрольную работу:
• сравнить количество допущенных ошибок:
• сделать выводы по использованию моделирования при решении задач.

Исследование проводилась два этапа:

1) входная диагностика;

2) контрольная диагностика.

В 2 б классе всего 11 учеников: три девочки и восемь мальчиков. Класс очень дружный, везде и во всем помогают друг другу. Я с ними работаю уже второй год, они пришли в первый класс разные по уровни знаний и даже по здоровью. Например, Нурмухаметов а Регина, Гайсин Радик, Ильгамов Арслан – старательные ученики, но они не могут самостоятельно решать задачи, так как они воспринимают лишь отдельные элементы задачи. Есть ученики, которые все знают, а сами не хотят учиться (Нурмухаметов Ранис, Закирова Эльмира).

Такие дети приходят на урок и сидят ничего не хотят делать. И моя задача состоялась в том, чтобы как-то заинтересовать их во время урока, привлечь внимание, вызвать живой интерес во время решения задач, воспитывать ответственность за начатое дело и потребность в его доведения до конца.

Урок математики не все дети любят. Иногда с некоторыми учащимися приходится заниматься индивидуально. Например, Мустафин Юлиан. Он второгодник, из-за своей болезни у него не развито логическое мышление, воображение. Юлиан не понимает условия задачи, но у него есть желание работать на доске, старается отвечать на вопросы учителя, хотя ответы не всегда правильны. Аетбаев Арсен и Мукуев Рамиль любят уроки математики, с удовольствием анализируют и решают задачи. Они плохо читают, на уровни 1 класса, но что интересно, эти мальчики слушают условия задачи, когда читает учитель или их товарищи и сразу же находят правильный ответ. У них хорошо развито мышление, умеют переходить от текста задачи к представлению ситуации. Делают чертеж к данной задаче и пишут решения. Ямалетдинов Ильгам отличается от своих товарищей тем, что он, прочитав условия задачи, сразу начинает рассказывать, что нам известно и что нужно найти. У него очень хорошо развито мышление, воображение и аккуратно выполняет графические построения к данной задачи.

2.3. Подведение итогов опытной работы и разработка методических рекомендаций для учителей по моделированию текстовых задач

Во время практики нами была проведена проверочная работа (приложение 1).

Результаты проверочной работы отражены в таблице 1, где знаком «+» отмечены правильно выполненные задания(приложение 2).

Из таблицы 1 видно, что дети имеют разные уровни знаний, умений и навыков:

один ученик — не выполнил 2 задание;

Четверо детей — не выполнили 1 задание;, Два ученика смогли решить только 1 задание;, Один испытуемый смог выполнить правильно все задачи.

На втором этапе нами было проведены занятия по математике с использованием алгоритмов (примерные конспекты уроков- приложение 4 ).

На заключительном – контрольном — этапе эксперимента мы провели письменную работу для определения глубины и прочности программных знаний, умений и навыков учащихся. (приложение 4).

Сравнивая результаты входного и контрольного этапов эксперимента можно заметить, что показатели знаний детей значительно улучшились.

Динамику изменения уровня знаний учащихся мы представили на диаграмме

1.На диаграмме отражено количество правильно выполненных во время проверочных работ заданий.

Чтобы доказать, что использование моделирования помогает при решении задач, была проведена соответствующая работа.

Входная диагностика.

Цель: выявить, насколько сформированы навыки решения задач у учащихся 2-х классов на исходном этапе эксперимента.

Для этого была предложена письменная работа. Каждый ученик должен был решить две задачи, которые ранее были порешены дома или в классе.

Задача 1.

Юлдың оҙонлоғо 100 м.Динислам менән Камил бер-береһенә ҡаршы йүгерәләр.Әгәр осрашҡанға тиклем Камил 50 метр йүгерһә, Динислам нисә метр йүгергән?

Задача 2.

Китапхана менән мәктәп араһы 50 м. Ә мәктәп менән медпункт араһы 25 м икәнлеге билдәле. Китапхана менән медпункт араһы нисә метр?

Несмотря на то,что задачи были знакомы, многие не справились с их решением и допустили большое количество ошибок.

Получены следующие результаты:

2 а класс:

1.Количество учащихся по списку-14

2.Выполняли работу-12

3.Выполнили всю работу без ощибок-4(33% )

4.Ошиблись в задаче №4-2 ученика(17% )

5.Ошиблись в задаче №2,№3,№4- 3 ученика (25%)

6.Не справились с работой -3(25%)

2 б класс:

1.Количество учащихся по списку-11

2.Выполняли работу-10

3.Выполнили всю работу без ошибок- (0%)

4.Ошиблись в задаче №2 -1 ученик(10%)

5.Ошиблись в задаче №3, №4 – 9 учеников (90%)

6.Не справились с работой 1 ученик (10%)

Класс

Качество знаний

Процент успеваемости

2 б

45%

95%

2 а

50%

90%

Из диаграммы в

Мы сделали такой вывод, что экспериментальной и контрольный классы написали данную работу примерно одинаково. На исходном этапе эксперимента навыки решения задач у учащихся 2 классов находятся на среднем уровне развития. Поэтому, мы поставили перед собой цель: систематически использовать моделирование при решении задач во 2 б классе.

Экспериментальному классу, предлагалось каждый урок решать задачи с использованием моделирования. В контрольном классе учащиеся не использовали модели при работе над задачей. Для этого были подобраны специальные упражнения, которые помогли бы детям овладеть умением моделирования.

Итоговая диагностика., Цель: выявление наличия или отсутствия умений решать задачи, используя метод моделирования.

Для этого предложена письменная работа. Каждый ученик должен был решить четыре задачи. Есть ученики, которые сделали по шесть заданий. У некоторых не все задачи правильные, хотя успели решать.

Задачи для письменной работы дано в приложение №1., Получены следующие результаты:

2 б класс (экспериментальный):

1.Количество учащихся по списку -14

2.Выполняли работу-10(из-за болезни отсутствовали-4 ученика)

3. Решили все задачи без ошибок-4 (40%)

4.Ошиблись в задаче №6 -3 ученика (30%)

5.Ошиблись в задаче №2, №3, №4,№5 -3 ученика (30%)

6. Не справились с решением задач -0

2 а класс(контрольный)

1.Количество учеников по списку -11

2.Выполняли работу – 10 (из-за болезни отсутствовал 1 ученик).

3.Решили все задачи без ошибок – 3 (30%)

4.Ошиблись в задаче №2, №3 -2 (20%)

5.Ошиблись в задаче №4, №5, №6 – 3(30%)

6.Не справились с решением задач -2 (20%), Таблица-диаграмма

Проанализировав данные результаты, можно сделать вывод, что экспериментальный класс выполнил работу намного лучше, чем контрольный. Дети в большинстве использовали модели при решении задач.

2 б класс (экспериментальный) показал более высокие результаты, чем 2 а класс (контрольный).

Сравнительная диаграмма 1.(экспериментальный- 2б класс), Сравнительная диаграмма 2.(контрольный – 2а класс)

Класс

Качество знаний

Процент успеваемости

2 б

70%

100%

2 а

50%

80%

Сравнительная диагностика 3.

У экспериментального класса (2б класс) уровень знаний повысился на 20%, а у контрольного класса (2 а класс) таком же состояние.

При решении задач следует использовать метод моделирования, что способствует сознательному и прочному усвоению и пониманию материала.

В процессе использования моделирования происходит углубление и развитие математического мышления учащихся. Поэтому моделирование –это один из ведущих методов обучения решению задач и важное средство познания действительности.

Методические рекомендации по организации работы над, Работая над текстовыми задачами, мы выработали следующие рекомендации:

1. Многие учащиеся только после повторного анализа осознают план решения задачи. Конечно, повторение анализа требует времени, но при решение текстовых задач результат будет положительным.

2. Необходимо анализировать готовое решение задачи.

3. Составление различных выражений по данным задачи; объяснение, что обозначает то или иное готовое выражение; выбор тех выражений, которые являются ответом на вопрос задачи.

4. Сравнения решений нескольких задач.

5. Запись двух решений на доске – одного верного и другого неверного.

6. Изменение вопроса задачи, без изменения условия; изменение условия, без изменения вопроса; изменение и того, и другого, ранее решенной

задачи.

7. Изменение условий задачи так, чтобы задача решалась другим действием, двумя или более действиями.

8. Завершение начатого решения задачи.

9. Определение лишнего или недостающего действия в решении задачи.

10. Составление аналогичной задачи с измененными данными.

Вывод по главе

Экспериментальная работа проводилась во 2 и 3 четверти 2014-2015 учебного года в 2 «а» и в 2 «б» классах МОБУ СОШ с. Ассы Белорецкого района. В исследовании принимали участие 25 человек. Оба класса работают по программе «Школа России».

2«а» — контрольная группа (11 человек).

2 «б» — экспериментальная группа (14 человек).

Цель эксперимента — выявить уровень развития математического мышления младших школьников.

Для достижения цели нашего исследования мы научили использовать моделирование при решение текстовых задач.

Данные, полученные в результате эксперимента, проанализированы., Итак, на основании полученных данных мы можем сделать следующие выводы:

1.У экспериментального класса (2б класс) уровень знаний повысился на 20%, а у контрольного класса (2 а класс) таком же состояние.

2.При решении задач следует использовать метод моделирования, что способствует сознательному и прочному усвоению и пониманию материала.

В процессе использования моделирования происходит углубление и развитие математического мышления учащихся. Поэтому моделирование –это один из ведущих методов обучения решению задач и важное средство познания действительности. Следовательно, наша гипотеза о том, что использование метода моделирования оказывает положительное влияние на развитие математического мышления младших школьников, получила подтверждение

Заключение

Я преподаю во 2 классе. Своей работе стремлюсь к тому, чтобы обучение было увлекательным, интересным для детей, помогало им в разных жизненных ситуация. Младший школьный возраст является началом формирования учебных действий у детей.

С помощью моделирования можно сделать объект более интересным и доступным для подробного изучения., Для чего же младшим школьникам необходимо уметь работать методом моделирования?, Во-первых, введение в содержание обучения понятий модели и

Во- вторых, целенаправленное и систематическое обучение методу моделирования приближает младших школьников к методам научного познания, обеспечивает их интеллектуальное развитие.

Для того чтобы научить учащихся работать с моделями нужно, чтобы школьники сами строили модели, сами изучали какие- либо объекты, явления с помощью моделирования.

Значительно

Мы считаем, что модель способна помочь не только найти способ решения задачи, но и проверить правильность решения, поскольку решение задачи разными способами – это один из видов такой проверки.

Использование графического моделирования при решении текстовых задач обеспечит более качественный анализ задачи, осознанный поиск ее решения, обоснованный выбор арифметических действий и предупредит многие ошибки в решении задач.

Модель задачи может быть использована для составления и решения обратных задач, для проведения исследования задачи. Модель помогает установить условия, при которых задача имеет решение или не имеет решения, помогает увидеть, как изменяется значение искомый величины в зависимости знаний.

Список использованной литературы:, Абдрахимова Л.Р, Абрамова О.М, Асадуллин Р.М, Баукина Л,В, Башмаков М. И,, Болотов В.А, Вильдман И.А, Быкова Т.П,, ВербицкийА.А,Кресловская Е.Е, Виноградов Н.Ф, Вольхин К.А, Лейбов А.М,, Граненова С.А, ДавыдоваЕ.А,, ДавыдоваЕ.А, Данилюк А.Я,, Дубова М.В, Ефимов В.Ф,, .Звонников В.И, Илюхин Б.В,, Кайл Роберт, .Мухамедьянов С.А,